Det vektor subtraktion eller vektor subtraktion mellem vektorer eller Y v betegnet med eller - v, beregnes ved at tilføje vektoren eller med vektoren modsat v. Algebraisk udtrykkes subtraktionen som følger:
eller - v = eller + (-v)
Det er muligt at udføre vektorsubtraktion ved at følge forskellige procedurer, for eksempel grafisk, på denne måde en vektor v tegnes af et orienteret linjesegment - en pil-.
Pilens længde svarer til modulet for vektoren, hældningen - i forhold til en given referencelinje - angiver retningen, og enden angiver vektorens retning.
Vektoren modsat v den har samme længde og retning, men den modsatte retning. Derefter, før du trækker mellem eller Y v, det er nødvendigt at tegne vektoren modsat v, og tilføj denne vektor til u.
Det er meget vigtigt at bemærke, at vektorsubtraktion ikke er kommutativ, det vil sige, at vektorernes rækkefølge ændrer resultatet, derfor:
eller - v ≠ v - eller
Den grafiske procedure kan udføres ved hjælp af en af disse metoder, hvis trin vi vil forklare nedenfor:
-Trekantsmetode.
-Parallelogram metode.
Artikelindeks
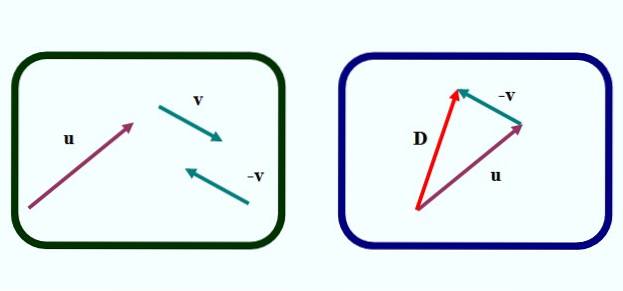
I figur 1 har vi den første af metoderne til at trække to vektorer grafisk. Det handler om trekantmetode, fordi figuren, der dannes ved at etablere vektorerne, er en trekant, som vi kan se på det venstre billede.
At udføre subtraktionen eller - v vi går frem som følger:
-Tegn vektoren -v fra vektor v, ved oversættelse med lineal og firkant, men ændring af pilens retning (venstre billede).
-Flytter til vektor -v på en sådan måde, at dens oprindelse falder sammen med enden af vektoren eller (højre billede).
-Dernæst tegnes en vektor (i rødt i det rigtige billede), der går fra oprindelsen af eller til slutningen af v. Opkald D y er forskellen vektor:
D = eller - v
I parallelogrammetoden skal vektorerne, der skal tilføjes eller trækkes, falde sammen på deres oprindelsessteder. Antag, at vi vil finde eller - v Med vores vektorer vist ovenfor er trinene til at finde subtraktion af vektorer ved denne metode som følger:
-Bestem modsat vektoren v, Hvad er det -v, som beskrevet ovenfor for trekantsmetoden.
-Oversæt omhyggeligt vektorer eller Y -v på en sådan måde, at deres oprindelse falder sammen.
-Nu tegnes segmenterede parallelle linjer startende fra enderne af hver vektor. Figuren, der dannes, er et parallelogram og i særlige tilfælde, hvor vektorerne er vinkelrette, resulterer et rektangel eller en firkant..
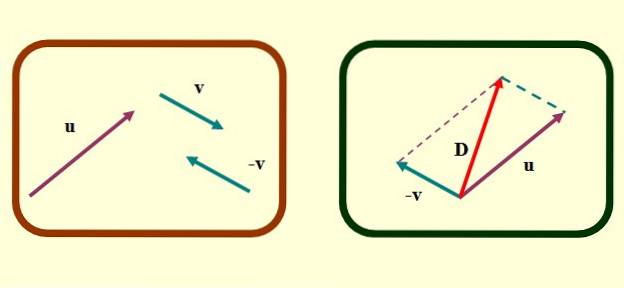
-Endelig tegnes en vektor, der starter fra den fælles oprindelse af eller Y v til det ekstreme, hvor de segmenterede parallelle linjer krydser hinanden. Dette er vektoren D eller subtraktion.
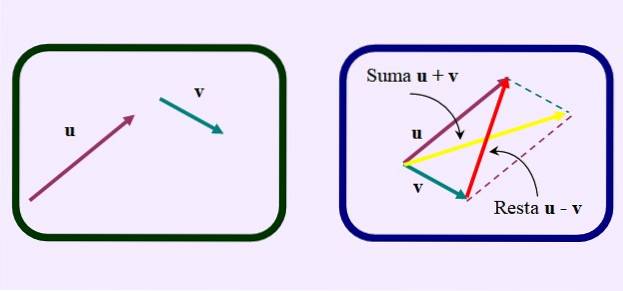
En anden måde at gøre subtraktionen på er at tegne parallelogrammet, som om du ville tilføje vektorerne.
Men i stedet for at tegne den sædvanlige diagonal af summen, der går fra den fælles oprindelse til skæringspunktet mellem parallellerne, modsat eller kortere diagonal, som det ses i figuren:
Et skib sejler på en flod og gør det i den modsatte retning af strømmen. En observatør på land bemærker, at bådens hastighed reduceres på grund af strømens handling.
Hastigheden er en vektor, og i dette eksempel peger bådens hastighed i en retning, og strømens hastighed har samme retning og modsat retning. Skibets nettohastighed er summen af begge vektorer.
For eksempel, hvis bådens instrumenter angiver, at den bevæger sig med v '= + 40 km / t, og en observatør på kysten måler, at båden bevæger sig med v = + 30 km / t. Da v = v '+ Vc, hvor Vc er strømhastigheden, der beregnes ved at trække henholdsvis hastighederne v og v': Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
I kinematik har vi vigtige vektorer, der beskriver ændringer:
-Offset for ændringer i position.
-Gennemsnitlig hastighed for at kvantificere, hvor hurtigt positionen varierer over tid.
-Acceleration til hastighedsændringer som en funktion af tiden.
Forskydningsvektoren beskriver den ændring i position, som en krop oplever under sin bevægelse.
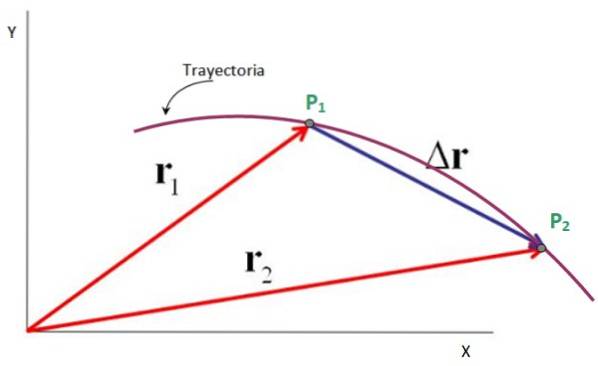
Lad os for eksempel se en partikel, der beskriver planstien vist i figuren, hvor den passerer fra punkt P1 til punkt Pto.
Vektorerne rettet fra oprindelsen af x-y-koordinatsystemet til disse punkter er positionsvektorerne r1 Y rto, mens forskydningsvektoren er Δr, der går fra P1 til Pto. Det er rigtigt, at:
Δr = rto - r1
Derfor er forskydningsvektoren subtraktionen mellem den endelige positionsvektor og den oprindelige positionsvektor som vist i den følgende figur. Dens enheder er også positionspositioner: meter, fødder, miles, centimeter og mere..
På sin side er den gennemsnitlige hastighedsvektor vm er defineret som forskydningen ganget med det inverse af tidsintervallet:
En partikel, der beskriver en cirkel, tager 5 s at passere fra punkt A til punkt B. Ved A har den en hastighed vTIL = 60 km / t mod + x-aksen og ved B er vB = 60 km / t mod + y. Bestem dens gennemsnitlige acceleration grafisk og analytisk.
I grafisk form bestemmes retning og retning af middelacceleration af:
I det følgende billede er subtraktionen vB - vTIL, ved hjælp af trekantsmetoden, siden den gennemsnitlige acceleration tilm er proportional med Δv. Den dannede trekant har de to ben ens, og derfor måler de akutte indvendige vinkler 45 ° hver..
Analytisk, hvis + x retningen falder sammen med enhedsvektoren jeg og + y-retningen med enhedsvektoren j, derefter:
Δv = 60 km / t j - 60 km / t jeg
At tage Δt = 5 s, ifølge oplysningerne i udsagnet, er den gennemsnitlige acceleration:
tilm = (60 km / t j - 60 km / t i) / 5 s = 12 (j-jeg) km / (h.s)
Endnu ingen kommentarer