
Halvcirkel, hvordan man beregner omkredsen, arealet, centroid, øvelser
Det halvcirkel er en plan figur afgrænset af en diameter på omkredsen og en af de to flade cirkelbuer bestemt af diameteren.
På denne måde er en halvcirkel omgivet af en halvcirkel, som består af en flad cirkelbue og et lige segment, der forbinder enderne af den flade cirkelbue. Halvcirklen omfatter halvcirklen og alle punkter inde i den..
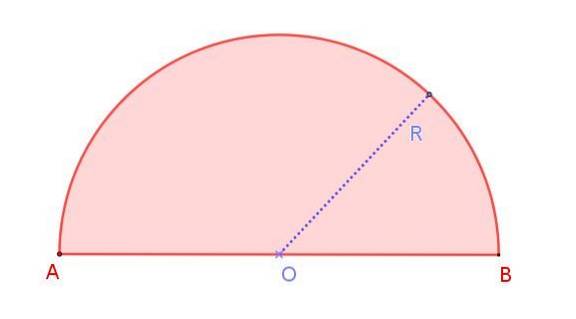
Vi kan se dette i figur 1, der viser en halvcirkel med radius R, hvis mål er halvdelen af diameteren AB. Bemærk, at i modsætning til en cirkel, hvor der er uendelige diametre, er der i halvcirkel kun en diameter.
Halvcirklen er en geometrisk figur med mange anvendelser inden for arkitektur og design, som vi ser på følgende billede:

Artikelindeks
- 1 Elementer og mål for en halvcirkel
- 1.1 Omkreds af en halvcirkel
- 1.2 Område af en halvcirkel
- 1.3 Midroid af en halvcirkel
- 1.4 Inerti-øjeblikket for en halvcirkel
- 1.5 Indskrevet vinkel
- 2 Løst øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 2.3 Øvelse 3
- 2.4 Øvelse 4
- 2.5 Øvelse 5
- 3 Referencer
Elementer og mål for en halvcirkel
Elementerne i en halvcirkel er:
1.- Det plane cirkelbue A⌒B
2.- Segmentet [AB]
3.- Punkterne inde i halvcirklen sammensat af buen A⌒B og segmentet [AB].
Omkreds af en halvcirkel
Omkredsen er summen af buens kontur plus den for det lige segment, derfor:
Perimeter = buelængde A⌒B + segmentlængde [AB]
I tilfælde af en halvcirkel med radius R vil dens omkreds P blive givet med formlen:
P = π⋅R + 2⋅R = (π + 2) ⋅R
Den første term er halvdelen af omkredsen af en cirkel med radius R, mens den anden er længden af diameteren, som er dobbelt så stor som radius..
Område af en halvcirkel
Da en halvcirkel er en af de plane vinkelsektorer, der forbliver, når der trækkes en diameter gennem omkredsen, vil dens område A være halvt arealet af cirklen, der indeholder halvcirklen med radius R:
A = (π⋅Rto) / 2 = ½ π⋅Rto
Midroid af en halvcirkel
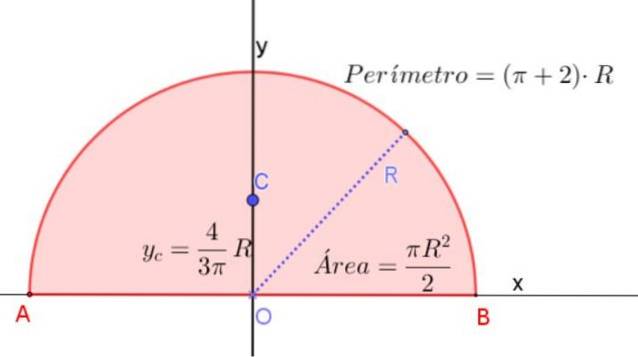
Halvcirkelens centrum er på symmetriaksen i en højde målt fra dens diameter på 4 / (3π) gange radius R.
Dette svarer til ca. 0,424⋅R målt fra midten af halvcirklen og på dens symmetriakse som vist i figur 3.
Inerti-øjeblikket for en halvcirkel
Inertimomentet for en plan figur i forhold til en akse, for eksempel x-aksen, defineres som:
Integralet af kvadratet for afstanden fra de punkter, der hører til figuren til aksen, integrationsforskellen er et uendeligt lille element af arealet taget ved hvert punkt.
Figur 4 viser definitionen af inertimomentet Ix af halvcirklen med radius R med hensyn til X-aksen, der passerer gennem dens diagonal:
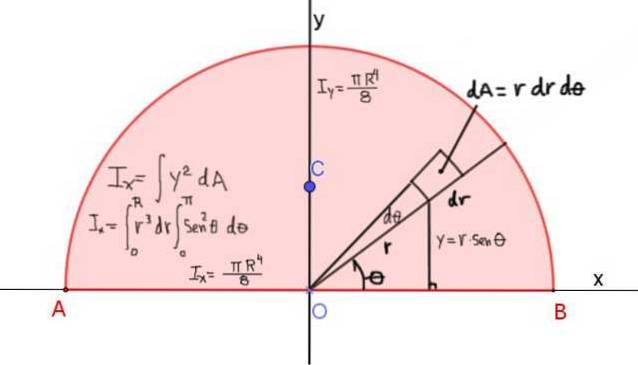
Trægemomentet omkring x-aksen er givet ved:
jegx = (π⋅R4) / 8
Og inertimomentet i forhold til symmetriaksen y er:
Iy = (π⋅R4) / 8
Det bemærkes, at begge inertimomenter falder sammen i deres formel, men det er vigtigt at bemærke, at de henviser til forskellige akser.
Indskrevet vinkel
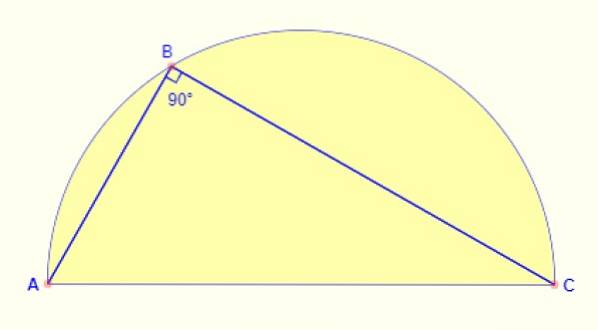
Vinklen indskrevet i halvcirklen er altid 90º. Uanset hvor punktet tages på buen, er vinklen, der dannes mellem siderne AB og BC, altid korrekt..
Løst øvelser
Øvelse 1
Bestem omkredsen af en halvcirkel med en radius på 10 cm.
Opløsning
Husk, at omkredsen som funktion af radius er givet ved den formel, vi så tidligere:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Øvelse 2
Find området for en halvcirkel med en radius på 10 cm.
Opløsning
Formlen for området af en halvcirkel er:
A = ½ π⋅Rto = ½ π⋅ (10 cm)to = 50π cmto = 50 x 3,14 cmto = 157 cmto.
Øvelse 3
Bestem højden h af centroid på en halvcirkel med radius R = 10 cm målt fra dens base, og halvcirkelens diameter er den samme.
Opløsning
Centroid er ligevægtspunktet for halvcirklen, og dens position er på symmetriaksen i en højde h fra basen (halvcirkelens diameter):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Øvelse 4
Find inertimomentet for en halvcirkel i forhold til aksen, der falder sammen med dens diameter, idet du ved, at halvcirklen er lavet af et tyndt ark. Dens radius er 10 cm og dens masse er 100 gram.
Opløsning
Formlen, der giver halvcirkelens inertimoment er:
jegx = (π⋅R4) / 8
Men da problemet fortæller os, at det er en materiel halvcirkel, skal den tidligere relation ganges med overfladetætheden af massen af halvcirklen, som vil blive betegnet med σ.
jegx = σ (π⋅R4) / 8
Derefter fortsætter vi med at bestemme σ, som ikke er noget andet end halvcirkelens masse divideret med dets areal.
Området blev bestemt i øvelse 2, og resultatet var 157 cmto. Derefter vil overfladetætheden for denne halvcirkel være:
σ = 100 gram / 157 cmto = 0,637 g / cmto
Derefter beregnes inertimomentet med hensyn til diameteren således:
jegx = (0,637 g / cmto) [3,1416 ⋅ (10 cm)4] / 8
Resulterer:
jegx = 2502 g⋅cmto
Øvelse 5
Bestem inertimomentet for en halvcirkel med en radius på 10 cm lavet af et materialeark med en overfladetæthed på 0,637 g / cmto langs en akse, der passerer gennem dens centroid og er parallel med dens diameter.
Opløsning
For at løse denne øvelse er det nødvendigt at huske Steiners sætning om inertimomenter af parallelle akser, som siger:
Inertimomentet I med hensyn til en akse, der er i en afstand h fra centroid er lig med summen af inertimomentet Ic i forhold til en akse, der passerer gennem centroid og er parallel med det første plus masseproduktet gange kvadratet for adskillelsen af de to akser.
Jeg = jegc + M hto
I vores tilfælde er jeg kendt, hvilket er inertimomentet med hensyn til diameteren, som allerede var beregnet i øvelse 4. Adskillelsen h mellem diameteren og centroid er også kendt, som blev beregnet i øvelse 3.
Vi skal kun rydde Ic:
jegc = I - M hto
jegc = 2502 g⋅cmto - 100 g 4.2 (4.246 cm)to giver som et resultat, at inertimomentet gennem en akse parallelt med diameteren og passerer gennem centroid er:
jegc = 699,15 g⋅cmto
Referencer
- Alexander, D. 2013. Geometri. 5. plads Udgave. Cengage læring.
- Math Open Reference. Halvcirkel. Gendannet fra: mathopenref.com.
- Universformler Halvcirkel. Gendannet fra: universoformulas.com.
- Universformler. Område af en halvcirkel. Gendannet fra: universoformulas.com.
- Wikipedia. Halvcirkel. Gendannet fra: en.wikipedia.com.



Endnu ingen kommentarer