
Aksiale symmetriegenskaber, eksempler og øvelser
Det aksial symmetri Det sker, når punkterne i en figur falder sammen med punkterne i en anden figur ved hjælp af en lige halveringslinje kaldet symmetriaksen. Det kaldes også radial, roterende eller cylindrisk symmetri..
Det anvendes normalt i geometriske figurer, men det kan let observeres i naturen, da der er dyr som sommerfugle, skorpioner, mariehøns eller mennesker, der præsenterer aksial symmetri..

Artikelindeks
- 1 Sådan finder du den aksiale symmetriske
- 2 Egenskaber ved aksial symmetri
- 3 Eksempler på aksial symmetri
- 4 Axiale symmetriøvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 4.3 Øvelse 3
- 4.4 Øvelse 4
- 5 Referencer
Sådan finder du aksial symmetrisk
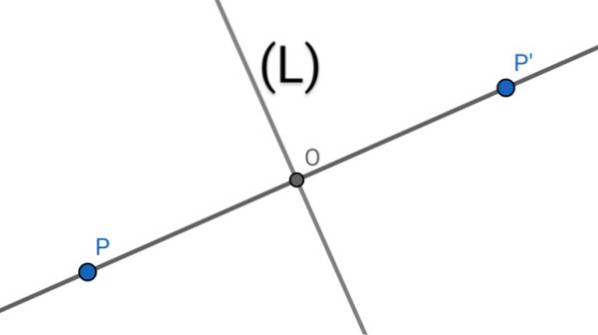
For at finde den aksiale symmetri P 'af et punkt P i forhold til en linje (L) udføres følgende geometriske operationer:
1. - Den vinkelrette på linjen (L), der passerer gennem punkt P, tegnes.
2.- Aflytningen af de to linjer bestemmer et punkt O.
3.- Længden af segmentet PO måles, så kopieres denne længde over linjen (PO) startende fra O i retning fra P til O, der bestemmer punktet P '.
4.- Punkt P 'er den aksiale symmetri af punkt P i forhold til aksen (L), da linjen (L) er mediatrixen for segmentet PP', hvor O er midtpunktet for nævnte segment.
Egenskaber ved aksial symmetri
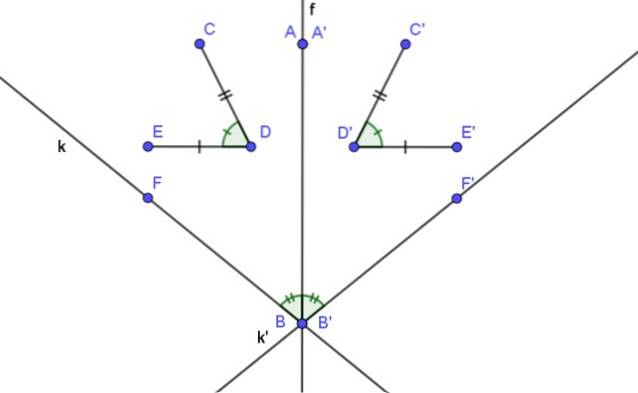
- Aksial symmetri er isometrisk, det vil sige afstanden til en geometrisk figur og dens tilsvarende symmetri bevares.
- Målingen af en vinkel og dens symmetriske er ens.
- Den aksiale symmetri af et punkt på symmetriaksen er selve punktet.
- Den symmetriske linje af en linje, der er parallel med symmetriaksen, er også en linje, der er parallel med aksen.
- En sekantlinie til symmetriaksen har som en symmetrisk linje en anden sekantlinie, der igen skærer symmetriaksen på det samme punkt af den oprindelige linje.
- Det symmetriske billede af en linje er en anden linje, der danner en vinkel med symmetriaksen af samme mål som den oprindelige linje.
- Det symmetriske billede af en linje vinkelret på symmetriaksen er en anden linje, der overlapper den første.
- En linje og dens aksiale symmetriske linje danner en vinkel, hvis halvering er symmetriaksen.
Eksempler på aksial symmetri
Naturen viser rigelige eksempler på aksial symmetri. For eksempel kan du se symmetrien af ansigter, insekter såsom sommerfugle, refleksionen på rolige vandoverflader og spejle eller planterne, blandt mange andre..


Aksiale symmetriøvelser
Øvelse 1
Vi har trekanten af hjørnerne A, B og C, hvis kartesiske koordinater er henholdsvis A = (2, 5), B = (1, 1) og C = (3,3). Find de kartesiske koordinater for trekanten symmetrisk omkring Y-aksen (ordinatakse).
Opløsning: Hvis et punkt P har koordinater (x, y), er dets symmetrisk omkring ordinataksen (Y-aksen) P '= (- x, y). Det vil sige, at værdien af dets abscissa ændrer tegn, mens ordinatens værdi forbliver den samme.
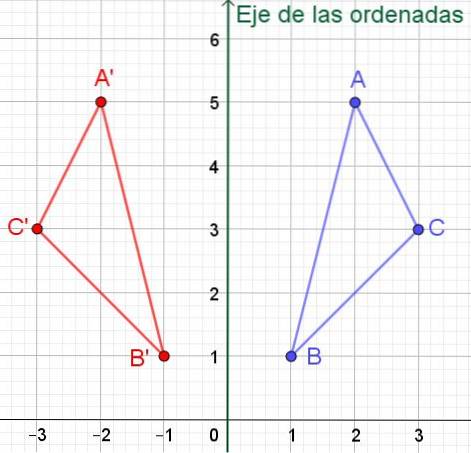
I dette tilfælde vil den symmetriske trekant med hjørnerne A ', B' og C 'have koordinater:
A '= (- 2, 5); B '= (- 1, 1) og C' = (- 3, 3) som det kan ses i figur 6.
Øvelse 2
Med henvisning til trekanten ABC og dens symmetriske A'B'C 'fra øvelse 1 skal du kontrollere, at de tilsvarende sider af den oprindelige trekant og dens symmetriske har samme længde.
Opløsning: For at finde afstanden eller længden af siderne bruger vi den euklidiske afstandsformel:
d (A, B) = √ ((Bx - Ax) ^ 2 + (By - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
Længden af den tilsvarende symmetriske side A'B 'beregnes nedenfor:
d (A ', B') = √ ((Bx'-Ax ') ^ 2 + (By'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4.123
På denne måde bekræftes det, at aksial symmetri bevarer afstanden mellem to punkter. Proceduren kan gentages for de to andre sider af trekanten og dens symmetriske for at kontrollere invariansen i længden. For eksempel | AC | = | A'C '| = √5 = 2.236.
Øvelse 3
I forhold til trekanten ABC og dens symmetriske A'B'C 'fra øvelse 1 skal du kontrollere, at de tilsvarende vinkler i den oprindelige trekant og dens symmetriske har samme vinkelmål.
Opløsning: For at bestemme målingerne af vinklerne BAC og B'A'C 'beregnes det skalære produkt af vektorerne først AB med AC og derefter prikproduktet af A'B ' med A'C '.
Husker det:
A = (2, 5), B = (1, 1) og C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) og C' = (- 3, 3).
Det har:
AB = <1-2, 1-5> Y AC = <3-2, 3-5>
på samme måde
A'B ' = <-1+2, 1-5> Y AC = <-3+2, 3-5>
Derefter findes følgende skalære produkter:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
Tilsvarende
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
Målingen af vinklen BAC er:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4.123-2.236)) = 40,6º
Tilsvarende er målingen af vinklen B'A'C ':
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4,123-22,236)) = 40,6º
Når man konkluderer, at aksial symmetri bevarer vinkelmålet.
Øvelse 4
Lad være et punkt P med koordinater (a, b). Find koordinaterne for dens aksiale symmetri P 'i forhold til linjen y = x.
Opløsning: Vi kalder (a ', b') koordinaterne for det symmetriske punkt P 'i forhold til linjen y = x. Midtpunktet M i segmentet PP 'har koordinater ((a + a') / 2, (b + b ') / 2) og er også på linjen y = x, så følgende ligestilling er sand:
a + a '= b + b'
På den anden side har segmentet PP 'hældning -1, fordi det er vinkelret på linjen y = x med hældning 1, så følgende ligestilling gælder:
b - b '= a' -a
Løsning for de to foregående lighed a 'og b' konkluderes, at:
a '= b og at b' = a.
Det vil sige, givet et punkt P (a, b), er dens aksiale symmetri i forhold til linjen y = x P '(b, a).
Referencer
- Arce M., Blázquez S og andre. Transformationer af flyet. Gendannet fra: educutmxli.files.wordpress.com
- Beregning cc. Aksial symmetri. Gendannet fra: calculo.cc
- Superprof. Aksial symmetri. Gendannet fra: superprof.es
- wikipedia. Aksial symmetri. Gendannet fra: es.wikipedia.com
- wikipedia. Cirkulær symmetri. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer