
System af ligninger løsningsmetoder, eksempler, øvelser
Det ecuationssystemer De består af to eller flere ligninger med flere variabler, der skal have en fælles løsning. De er hyppige, fordi der i praksis er mange situationer, der afhænger af mange faktorer, som er forbundet på forskellige måder.
Generelt har et ligningssystem følgende form, hvor hver funktion repræsenterer en af de betingelser, som opløsningen skal opfylde:

Lad os se et eksempel: Antag at du skal fremstille rektangulære papirark, hvis areal er 180 cmto og som har en omkreds på 54 cm. Hvad skal være arkets mål?
For at besvare spørgsmålet tager vi højde for, at dimensionerne på et rektangulært ark er to: bredde og højde. Dette betyder, at vi har 2 variabler, som vi giver de sædvanlige navne på x og Y.
Og disse variabler skal opfylde de to betingelser, der pålægges på samme tid:
-Første betingelse: arkets areal er 180 cmto. Dette vil være den første funktion: F1.
-Anden betingelse: arkets omkreds eller kontur skal være 54 cm. Dette er den anden funktion Fto.
For hver tilstand oprettes en ligning ved hjælp af algebraisk sprog. Området A på et rektangulært ark opnås ved at gange bredden med højden:
A = x.y = 180 cmto
Og omkredsen P skyldes tilføjelse af siderne. Da omkredsen er summen af siderne:
P = 2x + 2y = 54 cm
Det resulterende system med to ligninger og to ukendte er:
xy = 180
2 (x + y) = 54
Vi har brug for to tal, hvis produkt er 180, og det dobbelte produkt af deres sum er 54, eller hvad er det samme: tilsammen skal de give 27. Disse tal er 12 og 15.
I afsnittet om løste øvelser vil vi tilbyde den detaljerede metode til at finde disse værdier, i mellemtiden kan læseren let kontrollere ved at erstatte, at de effektivt tilfredsstiller begge ligninger.
Artikelindeks
- 1 Eksempler på anvendelser af ligningssystemer
- 2 Metoder til løsning af ligningssystemer
- 2.1 Erstatningsmetode
- 2.2 Metode til reduktion eller eliminering
- 2.3 Udligningsmetode
- 2.4 Grafisk metode
- 3 Øvelser
- 3.1 - Øvelse løst 1
- 3.2 - Øvelse løst 2
- 4 Referencer
Eksempler på anvendelser af ligningssystemer
Den ovenfor foreslåede situation indeholder 2 variabler, og der kræves mindst 2 ligninger for at finde dem. Der er systemer med mange flere variabler, men under alle omstændigheder, hvis systemet har n af dem kræver det i det mindste n ligninger uafhængige af hinanden (man kan ikke være en lineær kombination af de andre) for at finde løsningen, hvis den findes.
Med hensyn til applikationerne er de mange. Her er nogle, hvor ligningssystemer viser deres anvendelighed:
-Finde de strømme, der strømmer gennem et kredsløb ved hjælp af Kirchoffs love.
-I land- og lufttransport for at fastlægge afgangs- og ankomsttider.
-Find størrelsen af kræfter i dynamiske eller statiske systemer, der er genstand for flere interaktioner.
-At kende mængden af solgte varer i en bestemt periode eller i fabrikker for at bestemme dimensionerne på objekter, så de opfylder visse betingelser med hensyn til overflade eller volumen.
-Når man bestemmer, hvordan man skal fordele en kapital i forskellige investeringer.
-Fastlæg satserne for forskellige tjenester, for eksempel telekommunikation eller shows, og kend mængden af indsamlede penge (se løst eksempel 2)
Metoder til løsning af ligningssystemer
Metode udskiftning
-En ligning vælges, og en af variablerne løses.
-Så er vi nødt til at erstatte den ryddede variabel i en anden ligning. Derefter forsvinder denne variabel derfra, og hvis systemet har to ligninger og to ukendte, forbliver der en ligning med en variabel, der allerede kan løses.
-Hvis systemet har mere end to variabler, skal vi løse en tredjedel ukendt fra en anden ligning og også udskifte den.
Et eksempel på anvendelsen af denne metode er i løst øvelse 1.
Reduktions- eller eliminationsmetode
Denne metode består i at tilføje eller trække ligninger for at eliminere en eller flere variabler og kun efterlade en. For at gøre dette er det praktisk at multiplicere ligningerne med en faktor således, at når det tilføjes med en anden ligning, forsvinder det ukendte. Lad os se et eksempel:
3xto - Yto = 11
xto + 4yto = 8
Vi ganger den første ligning med 4:
12xto - 4yto = 44
xto + 4yto = 8
Ved at tilføje dem forsvinder det ukendte Y, resterende:
13xto = 52
xto = 4
Derfor x1 = 2 og xto = -2. Med disse værdier kan læseren kontrollere det og1 = 1 og yto = -1
Udligningsmetode
Når systemet er to ligninger med to ukendte:
-Vælg et ukendt og løs for begge ligninger.
-Resultaterne udlignes, hvilket giver mulighed for at opnå en enkelt ligning med en enkelt ukendt.
-Denne ligning er løst, og resultatet erstattes i en af de foregående frigange for at opnå værdien af den anden ukendte..
Denne metode vil blive anvendt i løst øvelse 2 i det følgende afsnit.
Grafisk metode
Denne metode består i at tegne kurver, som hver ligning repræsenterer. Skæringspunktet er løsningen på systemet. Følgende eksempel viser systemets grafiske løsning:
xto + Y to = 1
2x + 4y = 0
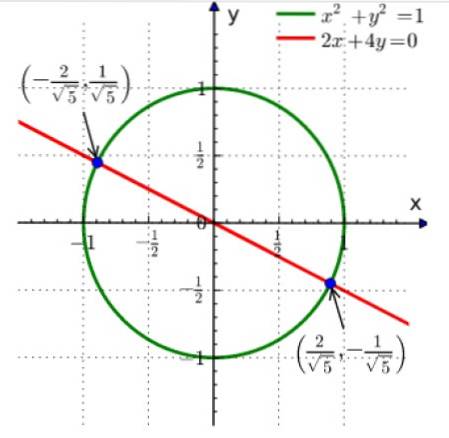
Den første af ligningerne er en cirkel med radius 1 centreret ved oprindelsen, og den anden er en linje.
Skæringspunktet mellem begge er de to punkter vist i blåt. Læseren kan verificere, at ved at erstatte koordinaterne for punkterne i ovenstående ligninger opnås en ligestilling.
Uddannelse
- Løst øvelse 1
Du skal fremstille rektangulære ark med et areal på 180 cmto og med en omkreds på 54 cm. Hvad skal arkets mål være?
Opløsning
Systemet, der skal løses, er:
xy = 180
2 (x + y) = 54
Den anden ligning kan forenkles til x + y = 27, derfor:
xy = 180
x + y = 27
Løs en af de ukendte i den anden ligning:
y = 27 - x
Clearance erstattes i det første:
(27 -x) = 180
Anvendelse af den distribuerende ejendom:
-xto + 27x = 180
Multiplikeres med (-1) på begge sider af ligningen og sende 180 til venstre side:
xto - 27x +180 = 0
Resultatet er en ligning af anden grad i x, som løses med formlen:

Med a = 1, b = -27 og c = 180

- Træning løst 2
En forlystelsespark har følgende adgangsgebyrer: børn $ 1,5 og voksne $ 4. På en dag var der 2.200 besøgende, hvilket samlede $ 5050. Find antallet af børn og voksne, der besøgte parken den dag.

Opløsning
Være x antallet af børn og Y antallet af voksne. Vi kan etablere den første af ligningerne ved at vide, at summen af begge skal være 2200:
x + y = 2200.
Nu går vi med de indsamlede penge. Prisen på børnebilletten er $ 1,5 for hvert barn, ved at gange denne værdi med x, antallet af børn, har vi beløbet for børnebilletten:
1,5x = penge indsamlet til børnebilletter
Og hvis vi gange $ 4 per voksen med antallet og antallet af voksne besøgende, får vi de samlede penge for alle voksne:
4y = penge indsamlet med voksenbilletter
Vi tilføjer dette sammen for at få $ 5050:
1,5x + 4y = 5050
Vores ligningssystem er:
x + y = 2200
1,5x + 4y = 5050
Lad os løse det ved udligning. Vi isolerer variablen y fra den første og den anden ligning:
y = 2200 - x
y = (5050 - 1,5 x) / 4
Vi matcher begge udtryk:
2200 - x = (5050 - 1,5x) / 4
Vi ganger alt med 4 for at eliminere brøken:
8800 - 4x = 5050 - 1,5x
Vi grupperer termerne med x til venstre og de rene tal til højre:
-4x + 1,5x = 5050 - 8800
-2,5x = -3750
x = 1500 børn.
Vi erstatter denne værdi i y = 2200 - x for at finde antallet af voksne:
y = 2200 - 1500 = 700 voksne.
Referencer
- CK-12. Systemer med ligninger og uligheder. Gendannet fra: ck12.org.
- Hoffman, J. Selection of Mathematics Topics. Bind 2.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Matematik til beregning. 5. plads Udgave. Cengage læring.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.



Endnu ingen kommentarer