
Tørstof med revolutionvolumen, typer, løste øvelser
Det solid af revolution Det er den tredimensionelle figur, der genereres ved at rotere en flad overflade omkring den aksiale akse eller omdrejningsaksen. Figur 1 viser en animation af et revolutionerende stof genereret på denne måde.
Et andet meget let at visualisere eksempel består i at generere en højre cirkulær cylinder, dreje et rektangel med højde eller længde h og radius r, omkring den positive x-akse (figur 2). For at finde dens volumen er der en velkendt formel:
V = areal af base x højde
Andre faste faste stoffer er sfæren, den rigtige cirkulære kegle og forskellige figurer, afhængigt af overfladen, der sættes i rotation og selvfølgelig den valgte akse..
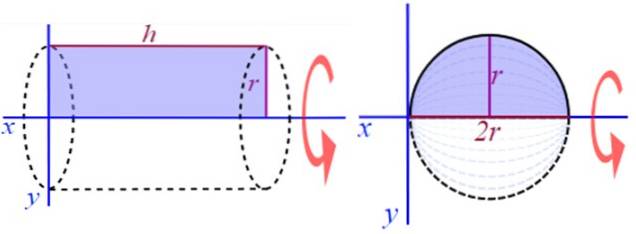
For eksempel drejer halvcirklen rundt om en linje, der er parallel med diameteren, et fast hulrum.
For cylinderen, keglen, kuglen, både solid og hul, er der formler til at finde volumen, som afhænger af radius og højde. Men når de genereres af andre overflader, beregnes lydstyrken med bestemte integraler.
Artikelindeks
- 1 Typer af faste faste stoffer
- 1.1 Sfære
- 1.2 Kegle
- 1.3 Cylinder
- 1.4 Toroid
- 2 Metoder til beregning af volumenet af et fast stof med revolution
- 2.1 Disk- eller vaskemetode
- 2.2 Lagmetode
- 3 Øvelse løst
- 4 Referencer
Typer af faste faste stoffer
Tørhedsgrader kan klassificeres efter kurven, der genererer dem:
Kugle
Det er nok at rotere en halvcirkel omkring en akse, der vil være diameteren af kuglen med radius R. Dens volumen er:
Vkugle = (4/3) πR3
Kegle
For at opnå en kegle med højden H og radius R er overfladen, der skal drejes, en ret trekant omkring den aksiale akse, der passerer gennem et af benene. Dens volumen er:
Vkegle = (1/3) πHRto
Cylinder
Når vi roterer et rektangel omkring en aksial akse, der passerer gennem en af siderne, som kan være den korte eller den lange side, får vi en højre cirkulær cylinder med radius R og højde H, hvis volumen er:
Vcylinder = πRtoH
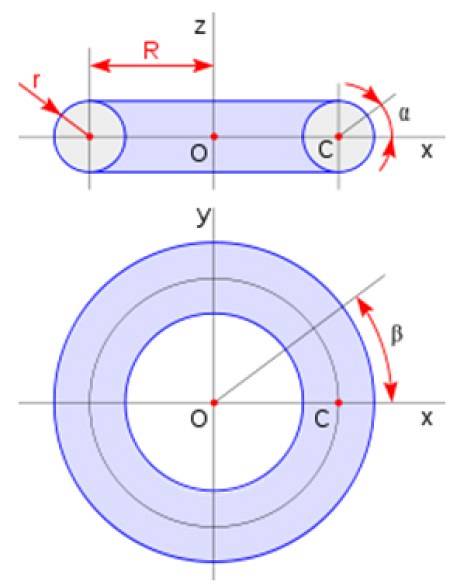
Toroid
Torus er formet som en doughnut. Det opnås ved at rotere et cirkulært område omkring en linje i planet, der ikke skærer cirklen. Dets volumen er givet af:
Vtorus = 2πatoR
Hvor a er tværsnitsradius, og R er radius for torus i henhold til skemaet vist i figuren:
Metoder til beregning af volumenet af et revolutionerende fast stof
I integreret beregning er disse to metoder hyppige:
-Skiver og skiver
-Skaller
Disk eller skive metode
Når der skives et revolutionsfast stof, kan tværsnittet være en skive, hvis det faste stof er solidt, eller det kan være en slags skive (en skive med et hul i midten), hvis det er et hult fast stof..
Antag, at en plan region roteres omkring den vandrette akse. Fra dette flade område tager vi et lille rektangel med bredden Δx, som roteres vinkelret omkring den aksiale akse.
Højden på rektanglet er mellem den yderste kurve R (x) og den inderste kurve r (x). De svarer til henholdsvis den ydre og den indre radius..
Ved at udføre denne rotation genereres en skive med volumen AV, givet ved:
ΔV = Fuld volumen - hulvolumen (hvis nogen)
Husk at volumenet af en højre cirkulær cylinder er π. radioto x højde, vi har:
AV = π [Rto(x) - rto(x)] Δx
Det faste stof kan opdeles i et væld af små volumendele AV. Hvis vi tilføjer dem alle, har vi den fulde lydstyrke.
For at gøre dette får vi lydstyrken ΔV til at være 0, hvormed Δx også bliver meget lille og bliver en differentiel dx.
Så vi har en integreret del:
V = ∫tilb π [Rto(x) - rto(x)] dx
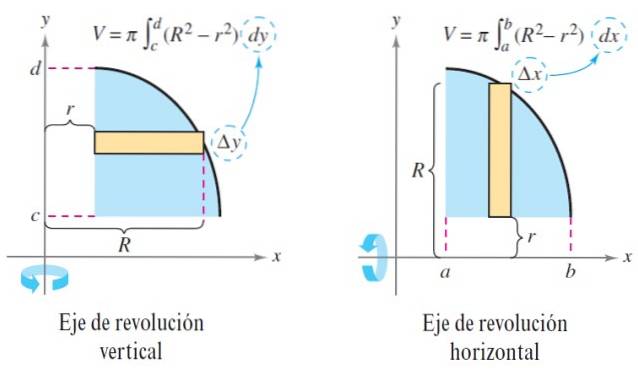
Hvis det faste stof er solidt, er funktionen r (x) = 0, skivet af det faste stof, der genereres, en disk, og lydstyrken forbliver:
V = ∫tilb πRto(x) dx
Når omdrejningsaksen er lodret, har ovenstående ligninger form:
V = ∫tilb π [Rto (y) - rto (y)] dy y V = ∫tilb πRto(y) dy
Lagmetode
Som navnet antyder, består denne metode i at antage, at det faste stof består af lag med forskellig tykkelse. Laget er et tyndt rør, der stammer fra rotationen af et rektangel parallelt med rotationsaksen.
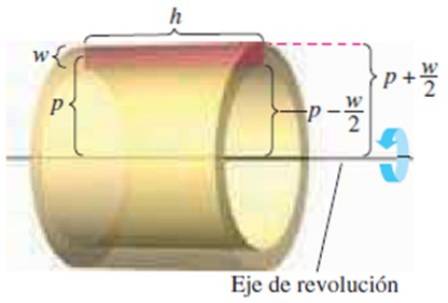
Vi har følgende dimensioner:
-Rektanglets højde w
-Dens længdegrad h
-Afstanden fra midten af rektanglet til rotationsaksen s
At vide, at lagets volumen er udvendigt volumen - indvendigt volumen:
π (p + w / 2)toh - π (p - w / 2)toh
Ved at udvikle bemærkelsesværdige produkter og forenkle får du:
Lagvolumen = 2π⋅p⋅w⋅h
Lad os nu lave højden w af rektanglet Δy, som det ses i følgende figur:
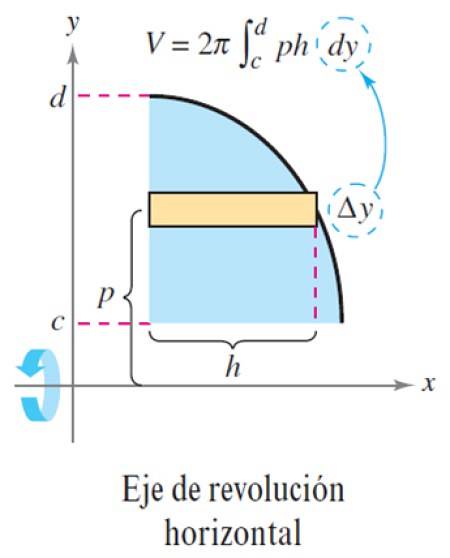
Med dette er lydstyrken ΔV:
ΔV = 2π p x h x Δy
Og lave antallet af lag n er meget stor, Δy bliver en differentiel dy, hvormed det samlede volumen er integralet:
V = ∫cd 2π p (y) h (y) dy
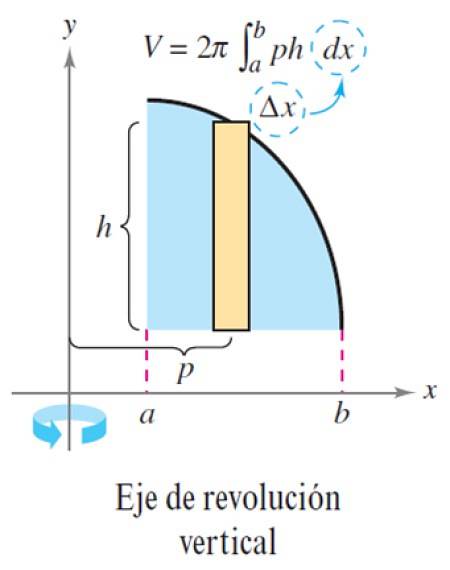
Den beskrevne procedure gælder på samme måde, når omdrejningsaksen er lodret:
Træning løst
Find det volumen, der genereres ved rotation af planområdet mellem kurverne:
y = xto; y = 0; x = 2
Omkring y-aksen.
Opløsning
-Den første ting, vi skal gøre, er at tegne en graf over det område, der genererer revolutionens faststof og angiver rotationsaksen. Vi har det i følgende graf:
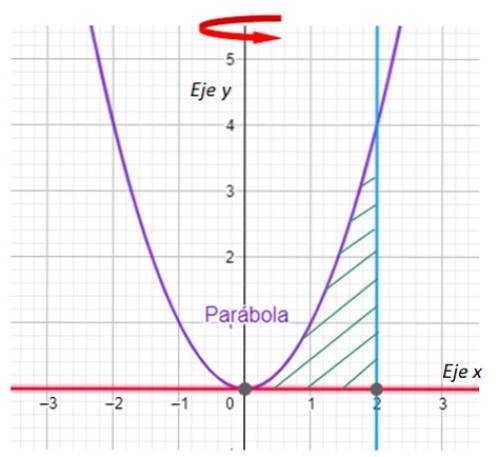
-Nu leder vi efter skæringspunkterne mellem kurven y = xto og linjen x = 2. For sin del er linjen y = 0 ingen ringere end x-aksen.
Fra grafen er det let at se, at parabolen og linjen krydser hinanden ved punktet (2,4), hvilket bekræftes ved at erstatte x = 2 i y = xto.
-Derefter vælges en af metoderne til beregning af lydstyrken, for eksempel lagmetoden med lodret omdrejningsakse:
V = ∫tilb 2π p (x) h (x) dx
Trin 1: tegne rektanglet
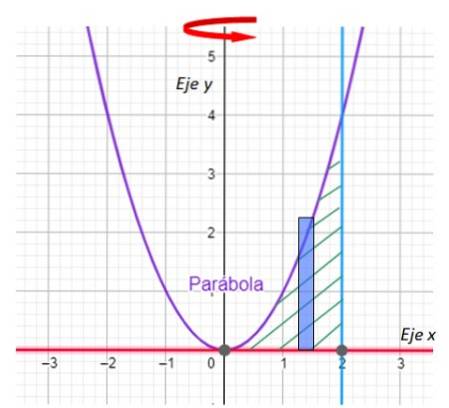
Vigtig: I lagdelingsmetoden er den lange side af rektanglet parallel med rotationsaksen.
Trin 2: Bestem p (x)
Lagets radius er x
Trin 3: Bestem h (x)
Rektanglets højde bestemmes af parabolen xto.
Trin 4: Opret og løs volumenintegralet
Integrationsvariablen er x, som varierer mellem 0 og 2, med dette har vi grænserne for integration. Udskiftning af udtryk for p (x) og h (x)

Referencer
- Larson, R. 2010. Beregning af en variabel. 9. Udgave. Mcgraw bakke.
- Purcell, E. 2007. Calculus med analytisk geometri. 9. Udgave. Pearson Uddannelse.
- Wikipedia. Solid af revolutionen. Gendannet fra: en.wikipedia.org.
- Wikipedia. Toroid Gendannet fra: es.wikipedia.org.
- Wolfram MathWorld. Solid af revolutionen. Gendannet fra: mathworld.wolfram.com.



Endnu ingen kommentarer