
Superposition teorem forklaring, anvendelser, løste øvelser
Det sætning med superposition, I elektriske kredsløb fastslår det, at spændingen mellem to punkter eller strømmen gennem dem er den algebraiske sum af spændingerne (eller strømme, hvis det er tilfældet) på grund af hver kilde, som om hver enkelt handlede på en anden måde Uafhængig.
Denne sætning giver os mulighed for at analysere lineære kredsløb, der indeholder mere end en uafhængig kilde, da det kun er nødvendigt at beregne bidraget fra hver enkelt separat..

Lineær afhængighed er afgørende for sætningen at anvende. Et lineært kredsløb er et, hvis svar er direkte proportionalt med indgangen.
For eksempel angiver Ohms lov, der gælder for en elektrisk modstand, at V = i.R, hvor V er spændingen, R er modstanden e jeg er den aktuelle. Det er derefter en lineær afhængighed af spænding og strøm i en modstand.
I lineære kredsløb anvendes superpositionsprincippet under hensyntagen til følgende:
-Hver uafhængig spændingskilde skal overvejes separat, og til dette er det nødvendigt at slukke for alle de andre. Det er nok at sætte til 0 V alle dem, der ikke er under analyse, eller at erstatte dem i skemaet med en kortslutning.
-Hvis kilden er aktuel, skal du åbne kredsløbet.
-Når man overvejer den interne modstand af både strøm- og spændingskilder, skal de forblive på plads og udgøre en del af resten af kredsløbet..
-Hvis der er afhængige kilder, skal de forblive, som de vises i kredsløbet.
Artikelindeks
- 1 Ansøgninger
- 2 trin til anvendelse af superpositionssætningen
- 3 Løst øvelser
- 3.1 - Eksempel 1
- 3.2 - Øvelse 2
- 4 Referencer
Ansøgninger
Superpositionssætningen bruges til at opnå enklere og lettere at håndtere kredsløb. Men det skal altid huskes, at det kun gælder for dem med lineære reaktioner, som sagt i begyndelsen.
Så det kan ikke bruges direkte til f.eks. Beregning af effekt, da effekt er relateret til strøm af:
P = ito R
Da strømmen er kvadreret, er svaret ikke lineært. Det gælder heller ikke for magnetiske kredsløb, der involverer transformere..
På den anden side giver superpositionssætningen mulighed for at kende den effekt, som hver kilde har på kredsløbet. Og selvfølgelig er det gennem dets anvendelse muligt at løse det fuldstændigt, det vil sige at kende strømme og spændinger gennem hver modstand.
Superpositionssætningen kan også bruges sammen med andre kredsløbssætninger, for eksempel Thévenins, til at løse mere komplekse konfigurationer..
I vekselstrømskredsløb er sætningen også nyttig. I dette tilfælde arbejder vi med impedanser i stedet for modstande, så længe den samlede respons for hver frekvens kan beregnes uafhængigt..
Endelig gælder sætningen i elektroniske systemer til både jævn- og vekselstrømsanalyse separat.
Trin til anvendelse af superpositionssætningen
-Deaktiver alle uafhængige kilder ved at følge instruktionerne i starten, undtagen den der skal analyseres.
-Bestem det output, enten spænding eller strøm, som den enkelte kilde producerer.
-Gentag de to trin, der er beskrevet for alle andre kilder.
-Beregn den algebraiske sum af alle bidrag, der er fundet i de foregående trin.
Løst øvelser
De udførte eksempler nedenfor præciserer brugen af sætningen i nogle enkle kredsløb.
- Eksempel 1
I kredsløbet vist i den følgende figur skal du finde strømmen gennem hver modstand ved hjælp af superpositionssætningen.
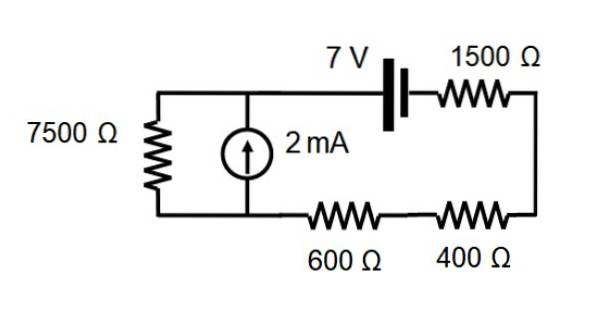
Opløsning
Spændingskildebidrag
Til at begynde med elimineres den aktuelle kilde, hvilket får kredsløbet til at se sådan ud:

Den ækvivalente modstand findes ved at tilføje værdien af hver modstand, da de alle er i serie:
7500 +600 +400 + 1500 Ω = 10.000 Ω
Anvendelse af Ohms lov V = I.R og rydde strømmen:
I = V / R = 7 / 10.000 A = 0.0007 A = 0,7 mA
Denne strøm er den samme for alle modstande.
Bidrag fra den aktuelle kilde
Spændingskilden elimineres straks for kun at arbejde med den aktuelle kilde. Det resulterende kredsløb er vist nedenfor:
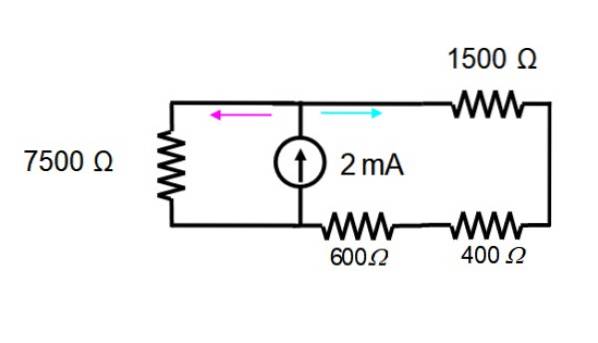
Modstandene på skærmen til højre er i serie og kan erstattes af en enkelt:
600 +400 + 1500 Ω = 2500 Ω
Det resulterende kredsløb ser sådan ud:
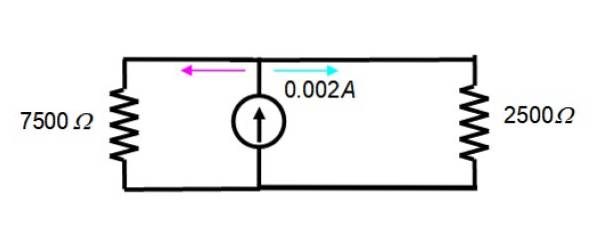
Strømmen på 2 mA = 0,002 A er delt mellem de to modstande i figuren, derfor er ligningen af den nuværende skillevæg gyldig:
jegx = (Rækv/ Rx) JegT
Hvor jegx er strømmen i modstanden Rx, Rækv symboliserer den tilsvarende modstand e jegT er den samlede strøm. Det er nødvendigt at finde den tilsvarende modstand mellem begge, velvidende at:
1 / Rækv = (1 / R.1) + (1 / R.to)
Derfor:
1 / Rækv = (1/7500) + (1/2500) = 1/1875 → Rækv = 1875 Ω
For dette andet kredsløb findes strømmen gennem 7500 Ω-modstanden ved at erstatte værdier i den nuværende divideringsligning:
jeg7500 Ω = (1875/7500). 0,002 A = 0,0005 A = 0,5 mA
Mens den, der passerer gennem 2500 Ω modstanden, er:
jeg2500 Ω = 2 mA - 0,5 mA = 1,5 mA
Anvendelse af superpositionssætningen
Nu anvendes superpositionssætningen for hver modstand, startende med 400 Ω:
jeg400 Ω = 1,5 mA - 0,7 mA = 0,8 mA
Vigtig: til denne modstand, strømmen trækkes fra, når de cirkulerer i den modsatte retning ifølge en omhyggelig observation af figurerne, hvor strømningenes retninger har forskellige farver.
Den samme strøm går ligeligt gennem 1500 Ω og 600 Ω modstandene, da de alle er i serie.
Teoremet anvendes derefter til at finde strømmen gennem 7500 Ω modstanden:
jeg7500 Ω = 0,7 mA + 0,5 mA = 1,2 mA
Vigtig: i tilfælde af 7500 Ω modstand, bemærk det strømmen tilføjes, fordi i begge kredsløb cirkulerer de i samme retning, når de passerer gennem denne modstand. Igen er det nødvendigt nøje at overholde strømningsretningerne.
- Øvelse 2
Finde strømmen og spændingen over 12 Ω modstanden ved hjælp af superpositionssætningen.
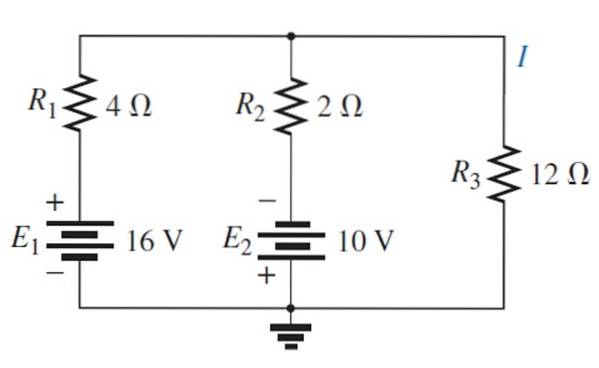
Opløsning
Font E erstattes1 med kortslutning:
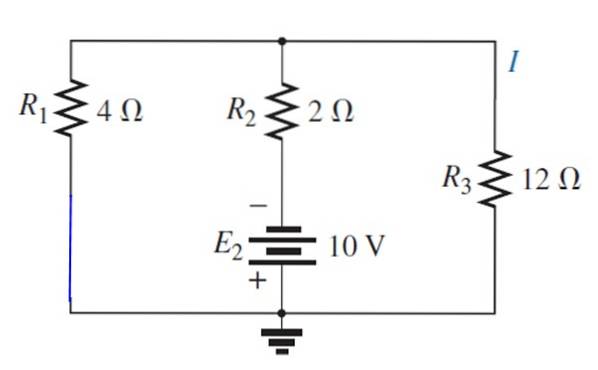
Det resulterende kredsløb tegnes som følger for let at visualisere de modstande, der forbliver parallelle:
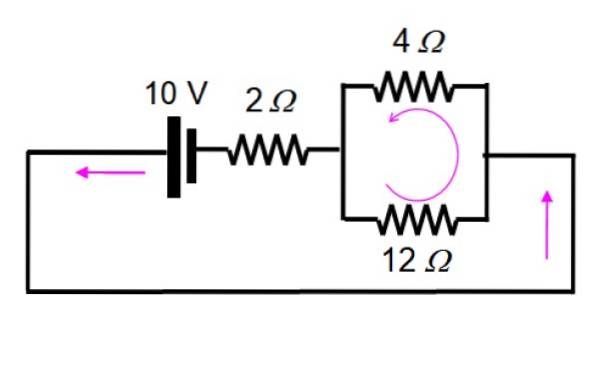
Og nu løses det ved at anvende serier og parallel:
1 / Rækv = (1/12) + (1/4) = 1/3 → Rækv = 3 Ω
Denne modstand er igen i serie med den af 2 Ω, derfor er den samlede modstand 5 Ω. Den samlede strøm er:
I = V / R = 10 V / 5 Ω = 2 A.
Denne strøm er opdelt som:
jeg12Ω = (3/12) 2 A = 0,5 A.
Derfor er spændingen:
V12Ω = 0,5 A × 12 Ω = 6 V
Nu er kilde E aktiveret1:
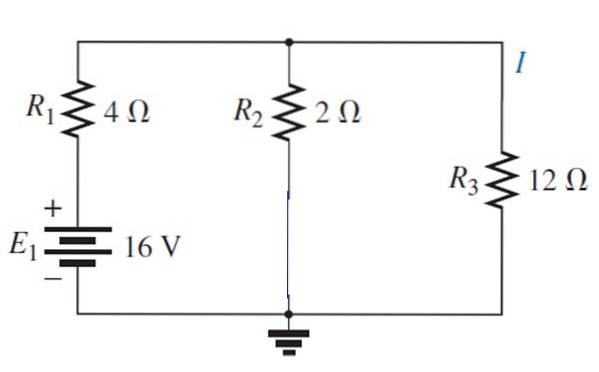
Det resulterende kredsløb kan tegnes således:

1 / Rækv = (1/12) + (1/2) = 7/12 → Rækv = 12/7 Ω
Og i serie med den af 4 Ω en tilsvarende modstandsresultat 40/7 Ω. I dette tilfælde er den samlede strøm:
I = V / R = 16 V / (40/7) Ω = 14/5 A.
Spændingsdeleren anvendes igen med disse værdier:
jeg12Ω = ((12/7) / 12) (14/5) A = 0,4 A.
Den resulterende strøm er: 0,5 - 0,4 A = 0,1 A. Bemærk, at de er blevet trukket, da strømmen fra hver kilde har en anden sans, som det kan ses i det originale kredsløb.
Spændingen over modstanden er:
V12Ω = 0,4 A × 12 Ω = 4,8 V
Endelig er den samlede spænding: 6V-4,8V = 1,2V
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 2. plads Udgave. Pearson.
- Dorf, R. 2006. Introduktion til elektriske kredsløb. 7. Udgave. John Wiley & Sons.
- Edminister, J. 1996. Elektriske kredsløb. Schaum-serien. 3. Udgave. Mc Graw Hill
- Wikipedia. Nuværende skillevæg. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer