
Thévenins sætning hvad den består af, applikationer og eksempler
Det Thévenins sætning angiver, at et kredsløb med terminalerne A og B kan erstattes af en ækvivalent, der består af en kilde og en seriemodstand, hvis værdier giver den samme potentialforskel mellem A og B og den samme impedans som det oprindelige kredsløb.
Denne sætning blev gjort kendt i 1883 af den franske ingeniør Léon Charles Thévenin, men det hævdes, at den blev forkyndt tredive år tidligere af den tyske fysiker Hermann von Helmholtz.

Dens nytte ligger i det faktum, at selvom det originale kredsløb er komplekst eller ukendt, med henblik på en belastning eller impedans, der er placeret mellem terminal A og B, opfører det enkle Thévenin-ækvivalente kredsløb sig på samme måde som originalen.
Artikelindeks
- 1 Hvordan beregner du den ækvivalente spænding trin for trin?
- 1.1 - Eksperimentelt
- 1.2 - Løsning af kredsløbet
- 2 Anvendelser af Thévenins sætning (del I)
- 2.1 Eksempel 1a (beregning af den ækvivalente spænding trin for trin)
- 2.2 Eksempel 1b (strøm i belastningen ved hjælp af Thévenin-ækvivalenten)
- 3 Bevis for Thévenins sætning
- 4 Anvendelse af Thévenins sætning (del II)
- 4.1 Eksempel 2a (Thévenin ækvivalent modstand)
- 4.2 Eksempel 2b
- 4.3 Eksempel 2c
- 5 Anvendelse af Thévenins sætning (del III)
- 5.1 Eksempel 3
- 6 Referencer
Hvordan beregner du den ækvivalente spænding trin for trin?
Spændingen eller potentialforskellen for det ækvivalente kredsløb kan opnås på følgende måder:
- Eksperimentelt
Opnåelse af den tilsvarende Thévenin-spænding
Hvis det er en enhed eller udstyr, der er i en “sort boks”, måles potentialforskellen mellem terminal A og B med et voltmeter eller et oscilloskop. Det er meget vigtigt, at der ikke placeres nogen belastning eller impedans mellem klemmerne A og B.
Et voltmeter eller et oscilloskop repræsenterer ingen belastning på terminalerne, da begge enheder har en meget stor impedans (ideelt set uendelig), og det ville være som om terminal A og B var uden belastning. Spændingen eller spændingen opnået på denne måde er den Thévenin ækvivalente spænding.
Opnåelse af Thévenins ækvivalente impedans
For at opnå den ækvivalente impedans fra en eksperimentel måling placeres en kendt modstand mellem klemmerne A og B, og spændingsfaldet eller spændingssignalet måles med et oscilloskop..
Fra spændingsfaldet i den kendte modstand mellem terminalerne kan den strøm, der strømmer gennem den, opnås.
Produktet af strømmen opnået med den ækvivalente modstand plus spændingsfaldet målt i den kendte modstand er lig med den ækvivalente Thévenin-spænding, der tidligere er opnået. Fra denne ligestilling ryddes den ækvivalente Thévenin-impedans.
- Løsning af kredsløbet
Beregning af den ækvivalente Thévenin-spænding
For det første frakobles enhver belastning eller impedans fra terminal A og B.
Som kredsløbet er kendt, anvendes netteori eller Kirchhoffs love for at finde spændingen ved terminalerne. Denne spænding svarer til Thévenin.
Beregning af Thévenin ækvivalent impedans
For at opnå den tilsvarende impedans går vi videre til:
- Udskift spændingskilderne i det originale kredsløb med kortslutninger "nul impedans" og de aktuelle kilder i det originale kredsløb med åbne "uendelig impedans".
- Derefter beregnes den ækvivalente impedans efter reglerne for serieimpedanser og parallelle impedanser.
Anvendelser af Thévenins sætning (del I)
Vi anvender Thévenins sætning til at løse nogle kredsløb. I denne første del betragter vi et kredsløb, der kun har spændingskilder og modstande.
Eksempel 1a (beregning af ækvivalent stress trin for trin)
Figur 2 viser kredsløbet, der er i en himmelboks, der har henholdsvis to elektromotoriske kraftbatterier V1 og V2 og modstande R1 og R2, kredsløbet har klemmer A og B, hvor en belastning kan forbindes.
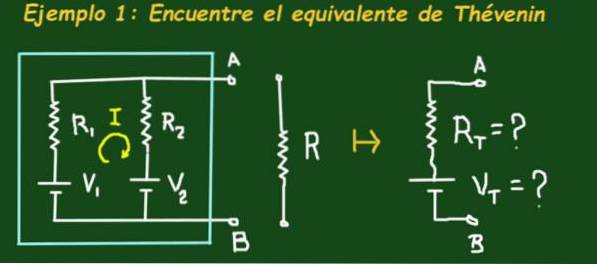
Målet er at finde det tilsvarende Thévenin-kredsløb, det vil sige at bestemme Vt- og Rt-værdierne for det ækvivalente kredsløb. Anvend følgende værdier: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω og R = 1Ω.
Trin for trin løsning
Trin 1
Vi bestemmer spændingen ved terminal A og B, når der ikke er belastning på dem.
Trin 2
Det kredsløb, der skal løses, består af et enkelt maske, gennem hvilket en strøm I cirkulerer, som vi har taget positivt med uret.
Trin 3
Vi går gennem masken startende med det nederste venstre hjørne. Stien fører til følgende ligning:
V1 - I * R1 - I * R2 - V2 = 0
Trin 4
Vi løser netstrømmen I og opnår:
I = (V1-V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Trin 5
Med netstrømmen kan vi bestemme spændingsforskellen mellem A og B, som er:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Det vil sige, at den ækvivalente spænding er: Vt = 3V.
Trin 6 (Thévenin ækvivalent modstand)
Vi fortsætter nu med at beregne Thévenin-ækvivalent modstand, for hvilken og som tidligere nævnt erstattes spændingskilderne med et kabel.
I så fald har vi kun to modstande parallelt, så Thévenins ækvivalente modstand er:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Eksempel 1b (strøm i belastningen ved hjælp af Thévenin-ækvivalenten)
Tilslut som belastning til klemmerne A og B en modstand R = 1Ω til det tilsvarende kredsløb og find den strøm, der strømmer gennem belastningen.
Opløsning
Når modstanden R er forbundet til Thevenin-ækvivalent kredsløb, har vi et simpelt kredsløb, der består af en kilde Vt en modstand Rt i serie med modstanden R.
Vi kalder Ic den strøm, der strømmer gennem belastningen R, så maske ligningen ser sådan ud:
Vt - Ic * Rt - Ic * R = 0
hvorfra det følger, at Ic er givet ved:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Bevis for Thévenins sætning
For at kontrollere, at Thévenins sætning holder, skal du slutte R til det originale kredsløb og finde strømmen, der flyder gennem R ved at anvende maskloven på det resulterende kredsløb.
Det resulterende kredsløb forbliver, og dets netværksligninger forbliver som vist i følgende figur:
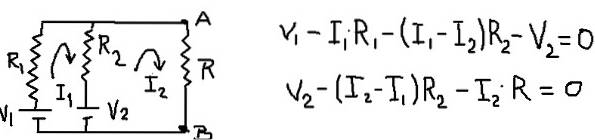
Ved at tilføje maske ligningerne er det muligt at finde maske strømmen I1 som en funktion af den aktuelle I2. Derefter erstattes den i den anden maske ligning, og en ligning efterlades med I2 som den eneste ukendte. Følgende tabel viser operationerne.
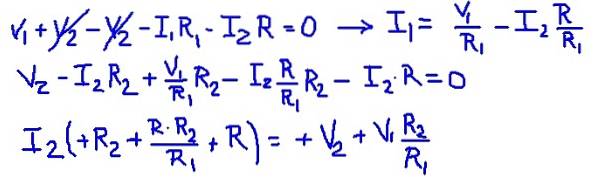
Derefter erstattes værdierne for kildens modstand og spændinger, hvilket får den numeriske værdi af netstrømmen I2.

Netstrømmen I2 er den strøm, der strømmer gennem belastningsmodstanden R, og værdien fundet af 1 A falder fuldt ud sammen med den, der tidligere blev fundet med det tilsvarende Thévenin-kredsløb..
Anvendelse af Thévenins sætning (del II)
I denne anden del anvendes Thévenin-sætningen i et kredsløb, der har spændingskilder, strømkilde og modstande.
Eksempel 2a (Thévenin ækvivalent modstand)
Formålet er at bestemme det Thévenin-ækvivalente kredsløb, der svarer til kredsløbet i den følgende figur, når terminalerne er uden modstand på 1 ohm, placeres modstanden og strømmen, der cirkulerer gennem den, bestemmes.
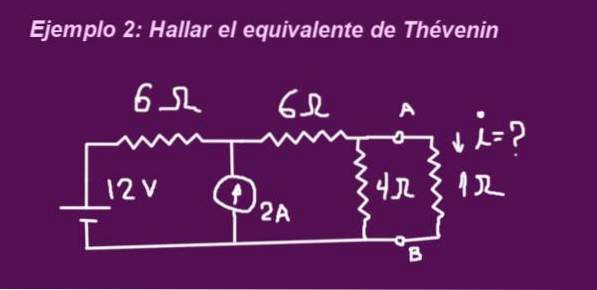
Opløsning
Fjern belastningsmodstanden (i dette tilfælde 1 ohm) for at finde den tilsvarende modstand. Spændingskilder erstattes også af en kortslutning og strømkilder af et åbent kredsløb..
På denne måde er kredsløbet, som den ækvivalente modstand beregnes for, det, der er vist nedenfor:
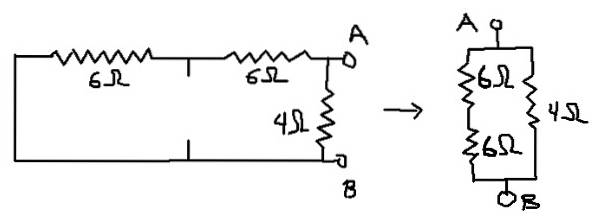
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω hvilket er Thevenin-ækvivalent modstand (Rth).
Eksempel 2b
Beregn Thévenins ækvivalente spænding.
Opløsning
For at beregne Thévenin-ækvivalent spænding betragter vi følgende kredsløb, hvor vi placerer strømmen i I1 og I2 i de grene, der er angivet i følgende figur:
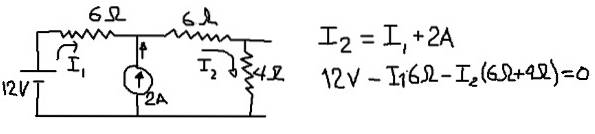
Den foregående figur viser ligningen af de aktuelle knudepunkter og ligningen af spændinger, når det eksterne maske krydses. Fra den anden af ligningerne ryddes den aktuelle I1:
I1 = 2 - I2 * (5/3)
Denne ligning er substitueret i ligningen af noderne:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Dette betyder, at spændingsfaldet over 4 ohm-modstanden er 6 volt..
Kort sagt er Thévenins spænding Vth = 6 V..
Eksempel 2c
Finde Thevenin-ækvivalent kredsløb og strøm i belastningsmodstanden.
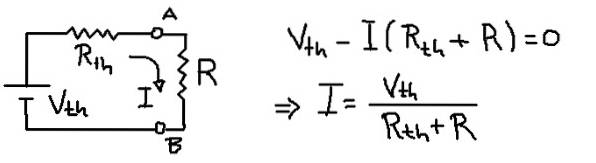
Opløsning
Den foregående figur viser Thévenin-ækvivalent kredsløb med belastningsmodstanden R. Fra spændingsligningen i masken udledes strømmen I, der strømmer gennem belastningsmodstanden R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Anvendelse af Thévenins sætning (del III)
I denne tredje del af anvendelsen af Thévenins sætning betragtes et vekselstrømskredsløb, der indeholder en vekselstrømskilde, en kondensator, en induktans og en modstand..
Eksempel 3
Målet er at finde Thévenin Circuit svarende til følgende kredsløb:
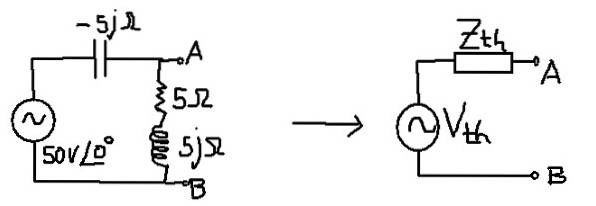
Opløsning
Den ækvivalente impedans svarer til kondensatorens parallel med seriekombinationen af modstand og induktans.
Omvendt af den tilsvarende impedans er givet ved:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Og den tilsvarende impedans vil så være:
Zeq = (1-3 j) Ohm
Den komplekse strøm I kan afledes fra maske ligningen:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Nu beregnes spændingsfaldet i modstanden plus induktansen, det vil sige spændingen Vab, som vil være den tilsvarende Thévenin-spænding:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Med andre ord har den ækvivalente spænding den samme topværdi af den oprindelige kilde, men er 45 grader ude af fase: Vth = 50V∠45º
Referencer
- Elektroniske vejledninger, Thevenins sætning. Gendannet fra: electronics-tutorials.ws
- Netværksteori spørgsmål og svar. Thevenins sætning. Gendannet fra: sanfoundry.com
- Thevenins sætning. Trin for trin procedure. Gendannet fra: electrictechnology.org
- Thevenins sætning. Løst eksempel trin for trin. Gendannet fra: electricalsimple.blogspot.com
- Workshop om Thevenins og Nortons sætninger. Gendannet fra: web.iit.edu
- Wikipedia. Thévenins sætning. Gendannet fra: wikipedia.com

Endnu ingen kommentarer