
Karakteristiske tessellationer, typer (regelmæssige, uregelmæssige), eksempler
Det tessellated er overflader dækket af en eller flere figurer kaldet fliser. De er overalt: i gader og bygninger af alle slags. Tessera eller fliser er flade stykker, generelt polygoner med kongruente eller isometriske kopier, som placeres efter et regelmæssigt mønster. På denne måde er der ingen mellemrum, der er afdækket, og fliserne eller mosaikkerne overlapper ikke hinanden..
I tilfælde af at der anvendes en enkelt type mosaik dannet af en regelmæssig polygon, er der en regelmæssig tessellation, men hvis der anvendes to eller flere typer regelmæssige polygoner, er det en semi-regelmæssig tessellation.

Endelig, når polygonerne, der danner tessellationen, ikke er regelmæssige, er det en uregelmæssig tessellation.
Den mest almindelige type tessellation er den, der dannes af rektangulære og især firkantede mosaikker. I figur 1 har vi et godt eksempel.
Artikelindeks
- 1 Historie om tessellationer
- 2 Almindelige tessellationer
- 2.1 Nomenklatur
- 2.2 Eksempel 1: Trekantet tessellation
- 2.3 Eksempel 2: Firkantet tessellation
- 2.4 Eksempel 3: Sekskantet tessellation
- 3 Semi-regelmæssige tessellationer
- 3.1 Eksempel 4: Tri-sekskantet tesselering
- 3.2 Eksempel 5: Stump sekskantet tessellation
- 3.3 Eksempel 6: rhombi-tri-sekskantet tessellation
- 4 Uregelmæssige tessellationer
- 4.1 Eksempel 7
- 4.2 Eksempel 8
- 4.3 Eksempel 9
- 4.4 Eksempel 10: Cairo-tessellation
- 4.5 Eksempel 11: Al-Andalus-tessellation
- 4.6 Eksempel 12: tessellation i videospil
- 5 Referencer
Tessellations historie
I tusinder af år er tessellation blevet brugt til at dække gulve og vægge i paladser og templer fra forskellige kulturer og religioner..
For eksempel den sumeriske civilisation, der blomstrede omkring 3500 f.Kr. syd for Mesopotamien, mellem Eufrat og Tigris-floderne, brugte de tessellationer i deres arkitektur.

Tessellations har også vækket interesse hos matematikere i alle aldre: begyndende med Archimedes i det 3. århundrede f.Kr. efterfulgt af Johannes Kepler i 1619, Camille Jordan i 1880, til nutid med Roger Penrose..
Penrose skabte en ikke-periodisk tessellation kendt som Penrose tessellation. OGDisse er blot nogle få navne på forskere, der bidrog meget med tessellering.
Regelmæssige tessellationer
Regelmæssige tessellationer foretages med kun en type regelmæssig polygon. På den anden side, for at tesselleringen kan betragtes som regelmæssig, skal hvert punkt i flyet:
-Tilhører det indre af polygon
-Eller til kanten af to tilstødende polygoner
-Endelig kan det høre til det fælles toppunkt på mindst tre polygoner.
Med ovenstående begrænsninger kan det vises, at kun ligesidede trekanter, firkanter og sekskanter kan danne en regelmæssig tessellation.
Nomenklatur
Der er en nomenklatur til at betegne tessellationer, der består i at angive med uret og adskilt af et punkt, antallet af sider af polygoner, der omgiver hver node (eller toppunkt) af tessellationen, altid startende med polygonen med det laveste tal. sider.
Denne nomenklatur gælder for regelmæssige og semi-regelmæssige tessellationer.
Eksempel 1: Trekantet tessellation
Figur 3 viser en regelmæssig trekantet tessellation. Det skal bemærkes, at hver knude i den trekantede tessellation er det fælles toppunkt på seks ligesidede trekanter.
Måden at betegne denne type tessellation er 3.3.3.3.3.3, som også er betegnet med 36.

Eksempel 2: Firkantet tessellation
Figur 4 viser en regelmæssig tessellation, der kun består af firkanter. Det skal bemærkes, at hver knude i tessellationen er omgivet af fire kongruente firkanter. Notationen, der anvendes på denne type firkantet tessellation, er: 4.4.4.4 eller alternativt 44

Eksempel 3: Sekskantet tessellation
I en sekskantet tesselering er hver knudepunkt omgivet af tre regelmæssige sekskanter som vist i figur 5. Nomenklaturen for en regelmæssig sekskantet tesselering er 6.6.6 eller alternativt 63.

Semi-regelmæssige tessellations
Semiregulære eller arkimediske tessellationer består af to eller flere typer regelmæssige polygoner. Hver knude er omgivet af de typer polygoner, der udgør tesselleringen, altid i samme rækkefølge, og kanttilstanden deles fuldstændigt med naboen..
Der er otte semi-regelmæssige tessellationer:
- 3.6.3.6 (tre sekskantet tessellation)
- 3.3.3.3.6 (stump sekskantet tessellation)
- 3.3.3.4.4 (aflang trekantet tessellation)
- 3.3.4.3.4 (stump firkantet tessellation)
- 3.4.6.4 (rhombi-tri-hexagonal tessellation)
- 4.8.8 (afkortet firkantet tessellation)
- 3.12.12 (trunkeret sekskantet tessellation)
- 4.6.12 (trunkeret triheksagonal tessellation)
Nogle eksempler på semi-regelmæssige tessellationer er vist nedenfor.
Eksempel 4: Tri-sekskantet tessellation
Det er den, der er sammensat af ligesidede trekanter og regelmæssige sekskanter i 3.6.3.6-strukturen, hvilket betyder, at en knude i tessellationen er omgivet (indtil en omgang er afsluttet) af en trekant, en sekskant, en trekant og en sekskant. Figur 6 viser en sådan tessellation.

Eksempel 5: Stump sekskantet tessellation
Ligesom tessellationen i det foregående eksempel består denne også af trekanter og sekskanter, men deres fordeling omkring en node er 3.3.3.3.6. Figur 7 illustrerer tydeligt denne type tessellation.

Eksempel 6: rhombi-tri-sekskantet tessellation
Det er en tessellation, der består af trekanter, firkanter og sekskanter i konfigurationen 3.4.6.4, som er vist i figur 8.
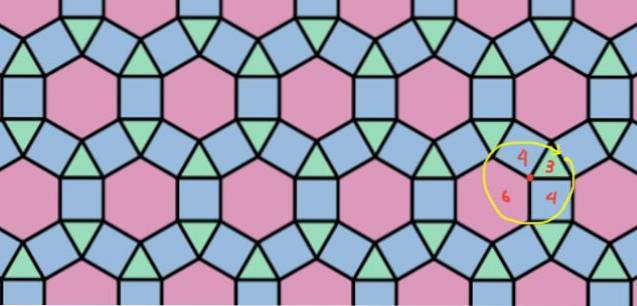
Uregelmæssige tessellationer
Uregelmæssige tessellationer er dem, der er dannet af uregelmæssige polygoner eller af regelmæssige polygoner, men som ikke opfylder kriteriet om, at en node er et toppunkt på mindst tre polygoner.
Eksempel 7
Figur 9 viser et eksempel på uregelmæssig tessellation, hvor alle polygoner er regelmæssige og kongruente. Det er uregelmæssigt, fordi en node ikke er et fælles toppunkt på mindst tre firkanter, og der er også tilstødende firkanter, der ikke helt deler en kant.
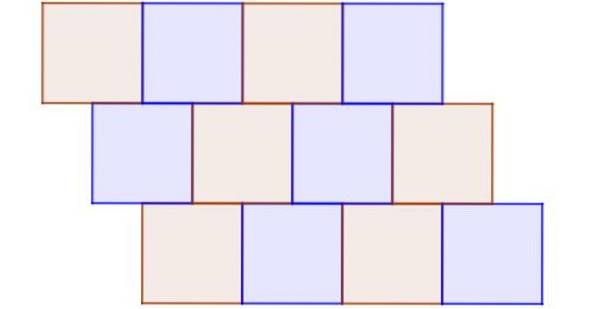
Eksempel 8
Parallellogrammet fliser en flad overflade, men medmindre den er en firkant, kan den ikke danne en regelmæssig tessellation.

Eksempel 9
Ikke-regelmæssige sekskanter med central symmetri tessellerer en flad overflade, som vist i følgende figur:

Eksempel 10: Cairo-tessellation
Det er en meget interessant tessellation, der består af pentagoner med lige lange sider, men med ulige vinkler, hvoraf to er lige og de andre tre har 120 ° hver..
Navnet stammer fra det faktum, at denne tessellation findes på fortovet i nogle af gaderne i Kairo i Egypten. Figur 12 viser afskærmningen af Kairo.

Eksempel 11: Al-Andalus-tessellation
Tessellationen i nogle dele af Andalusien og Nordafrika er præget af geometri og epigrafi ud over ornamentale elementer som vegetation..
Tessellationen af paladser som Alhambra bestod af fliser bestående af keramiske stykker i mange farver med flere (hvis ikke uendelige) former, der frigav geometriske mønstre..

Eksempel 12: tessellation i videospil
Også kendt som tesellation, det er en af de mest populære nyheder i videospil. Det handler om oprettelse af teksturer for at simulere afbrydelsen af de forskellige scenarier, der vises i simulatoren.
Dette er den klare refleksion, at disse belægninger fortsætter med at udvikle sig og krydser grænserne for virkeligheden..
Referencer
- Nyd matematik. Tessellations. Gendannet fra: gustolasmatematicas.com
- Rubiños. Tessellations løste eksempler. Gendannet fra: matematicasn.blogspot.com
- Weisstein, Eric W. "Demiregular tessellation". Weisstein, Eric W, red. MathWorld. Wolfram Research.
- Wikipedia. Tessellation. Gendannet fra: es.wikipedia.com
- Wikipedia. Regelmæssig tessellation. Gendannet fra: es.wikipedia.com


Endnu ingen kommentarer