
Skrå parabolske skudegenskaber, formler, ligninger, eksempler
Det skråt parabolsk skud er et særligt tilfælde af frit faldbevægelse, hvor projektilets indledende hastighed danner en bestemt vinkel med vandret, hvilket resulterer i en parabolsk bane.
Frit fald er et tilfælde af bevægelse med konstant acceleration, hvor accelerationen er tyngdekraften, som altid peger lodret nedad og har en styrke på 9,8 m / s ^ 2. Det afhænger ikke af projektilets masse, som Galileo Galilei viste i 1604.
Hvis projektilens indledende hastighed er lodret, har det frie fald en lige og lodret bane, men hvis den indledende hastighed er skrå, så er banen for frit fald en parabolsk kurve, en kendsgerning, der også demonstreres af Galileo.
Eksempler på parabolsk bevægelse er en baseballs bane, kuglen affyret fra en kanon og vandstrålen, der kommer ud af en slange..
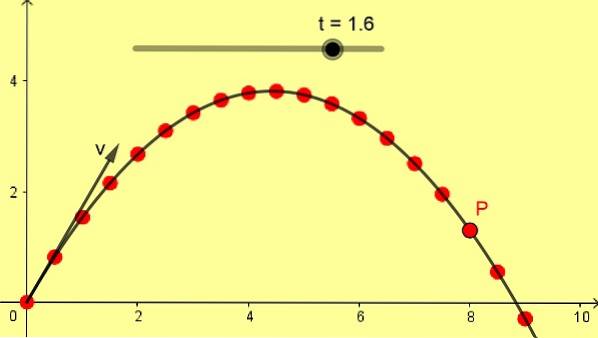
Figur 1 viser et skråt parabolsk træk på 10 m / s med en vinkel på 60º. Skalaen er i meter, og de successive positioner for P tages med en forskel på 0,1 s startende fra det første øjeblik 0 sekunder.
Artikelindeks
- 1 Formler
- 1.1 Position og hastighed
- 2 ligninger
- 2.1 Parametriske ligninger
- 2.2 Ligning af banen
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 3.3 Eksempel 3
- 4 Referencer
Formler
Bevægelsen af en partikel er beskrevet fuldt ud, hvis dens position, dens hastighed og dens acceleration er kendt som en funktion af tiden..
Den parabolske bevægelse som følge af et skråt skud er overlejringen af en vandret bevægelse ved konstant hastighed plus en lodret bevægelse med konstant acceleration svarende til tyngdeacceleration..
Formlerne, der gælder for det skrå parabolske træk, er dem, der svarer til en bevægelse med konstant acceleration a = g, bemærk, at fed er blevet brugt til at indikere, at accelerationen er en vektormængde.
Position og hastighed
I en bevægelse med konstant acceleration afhænger positionen matematisk af tiden i kvadratisk form.
Hvis vi betegner r(t) position på tidspunktet t, reller positionen i det første øjeblik, veller indledende hastighed, g acceleration og t = 0 som det første øjeblik den formel, der giver positionen for hvert øjeblik t det er:
r(t) = reller + veller t + ½ g tto
Fed skrift i ovenstående udtryk angiver, at det er en vektorligning.
Hastigheden som funktion af tiden opnås ved at tage afledningen i forhold til positionens t, og resultatet er:
v(t) = veller + g t
Og for at opnå accelerationen som en funktion af tiden, afledningen af hastigheden i forhold til t resulterer:
til(t) = g
Når tiden ikke er tilgængelig, er der et forhold mellem hastighed og position, som er givet ved:
vto = vellerto - 2 g (og - mig)
Ligninger
Dernæst finder vi ligningerne, der gælder for et skråt parabolsk skud i kartesisk form.
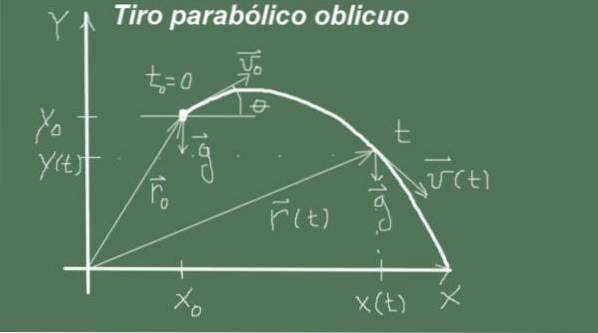
Bevægelsen begynder i øjeblikket t = 0 med startposition (xo, mig) og størrelseshastighed veller og vinkel θ, den indledende hastighedsvektor er (veller cosθ, veller senθ). Bevægelsen fortsætter med acceleration
g = (0, -g).
Parametriske ligninger
Hvis vektorformlen, der giver positionen som en funktion af tiden, anvendes og komponenter grupperes og udlignes, opnås ligningerne, der giver koordinaterne til positionen på ethvert tidspunkt af tidspunktet t.
x (t) = xeller + vokse t
y (t) = yeller + vHej t -½ g tto
På samme måde har vi ligningerne for hastighedskomponenterne som en funktion af tiden.
vx(t) = vokse
vY(t) = vHej - g t
Hvor: vokse = veller cosθ; vHej = veller senθ
Ligning af banen
y = A x ^ 2 + B x + C
A = -g / (2 vokse^ 2)
B = (vHej/ vokse + g xeller/ vokse^ 2)
C = (ogeller - vHej xeller / vokse)
Eksempler
Eksempel 1
Svar på følgende spørgsmål:
a) Hvorfor i parabolske trækproblemer bliver effekten af friktion med luft normalt forsømt??
b) Har objektets form nogen betydning i det parabolske skud?
Svar
a) For at et projektils bevægelse skal være parabolsk, er det vigtigt, at luftens friktionskraft er meget mindre end vægten af det objekt, der kastes.
Hvis en kork kugle eller noget let materiale kastes, er friktionskraften sammenlignelig med vægten, og dens bane kan ikke nærme sig en parabel.
Tværtimod, hvis det er en tung genstand som en sten, er friktionskraften ubetydelig sammenlignet med vægten af stenen, og dens bane nærmer sig en parabel.
b) Formen på den kastede genstand er også relevant. Hvis et ark papir kastes i form af et fly, vil dets bevægelse ikke være frit fald eller parabolsk, da formen favoriserer luftmodstand.
På den anden side, hvis det samme ark papir komprimeres til en kugle, er den resulterende bevægelse meget lig en parabel.
Eksempel 2
Et projektil lanceres fra vandret underlag med en hastighed på 10 m / s og en vinkel på 60º. Dette er de samme data, som figur 1 blev uddybet med. Med disse data, find:
a) Øjeblik, hvor den når den maksimale højde.
b) Den maksimale højde.
c) Hastighed ved maksimal højde.
d) Position og hastighed ved 1,6 s.
e) I det øjeblik det rammer jorden igen.
f) Den vandrette rækkevidde.
Løsning til)
Den lodrette hastighed som funktion af tiden er
vY(t) = vHej - g t = veller sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
I det øjeblik den maksimale højde nås, er den lodrette hastighed nul et øjeblik.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Løsning b)
Den maksimale højde er angivet af koordinaten Y i det øjeblik, hvor højden nås:
og (0,88s) = I + go t -½ g t ^to = 0 + 8,66 * 0,88-½ 9,8 0,88 ^to =
3,83 m
Derfor er den maksimale højde 3,83 m.
Løsning c)
Hastigheden ved maksimal højde er vandret:
vx(t) = vokse = veller cosθ = 10 cos60º = 5 m / s
Løsning d)
Positionen ved 1,6 s er:
x (1,6) = 5 * 1,6 = 8,0 m
og (1.6) = 8,66 * 1,6-½ 9,8 1,6to = 1,31 m
Løsning e)
Når y-koordinaten berører jorden, så:
y (t) = 8,66 * t-½ 9,8 tto = 0 ⇒ t = 1,77 s
Løsning f)
Den vandrette rækkevidde er x-koordinaten lige i det øjeblik den berører jorden:
x (1,77) = 5 * 1,77 = 8,85 m
Eksempel 3
Find ligningen af banen med dataene fra eksempel 2.
Opløsning
Den parametriske ligning af stien er:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^to
Og den cartesiske ligning opnås ved at løse t fra den første og erstatte den anden
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^to
Forenkling:
y = 1,73 x - 0,20 x ^ 2
Referencer
- P. P. Teodorescu (2007). "Kinematik". Mekaniske systemer, klassiske modeller: partikelmekanik. Springer.
- Resnick, Halliday & Krane (2002). Fysik bind 1. Cecsa, Mexico.
- Thomas Wallace Wright (1896). Elementer af mekanik inklusive kinematik, kinetik og statik. E og FN Spon.
- Wikipedia. Parabolsk bevægelse. Gendannet fra es.wikipedia.org.
- Wikipedia. Projektilbevægelse Gendannet fra en.wikipedia.org.


Endnu ingen kommentarer