Det lodret skud Det er en bevægelse, der finder sted under påvirkning af et kraftfelt, ofte tyngdekraften, og som kan være stigende eller nedadgående. Det er også kendt under navnet lodret lancering.
Det mest øjeblikkelige eksempel er at kaste en kugle op (eller ned, hvis du foretrækker det), selvfølgelig og sørg for at gøre det i lodret retning. Bortset fra luftmodstand passer bevægelsen, som kuglen følger, perfekt til modellen Uniformly Varied Rectilinear Motion (MRUV)..
Det lodrette skud er en bevægelse, der er bredt undersøgt i indledende fysik kurser, da det er et eksempel på bevægelse i en dimension, en meget enkel og nyttig model.
Denne model kan ikke kun bruges til at studere kinematikken af genstande under tyngdekraftens indvirkning, men beskriver også, som det vil fremgå senere, bevægelsen af partikler midt i et ensartet elektrisk felt..
Artikelindeks
Det første, der er behov for, er et koordinatsystem, der angiver oprindelsen og mærker det med et bogstav, hvilket i tilfælde af lodrette bevægelser er bogstavet "Y".
Derefter vælges den positive retning +Y, som normalt er opad og sansen -Y som normalt tages ned (se figur 2). Alt dette, medmindre problemløseren beslutter andet, da en anden mulighed er at tage bevægelsens retning som positiv, uanset hvad den måtte være..
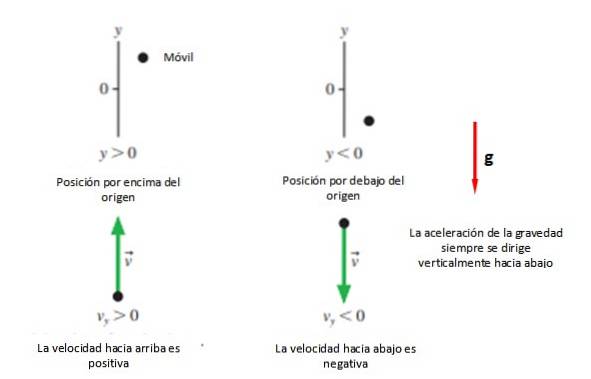
Under alle omstændigheder anbefales det, at oprindelsen falder sammen med startpunktet. Yeller, fordi denne måde ligningerne er forenklet, selvom du kan indtage en hvilken som helst position, du vil begynde at studere bevægelsen.
Når vi først har etableret koordinatsystemet og oprindelsen, går vi til ligningerne. Størrelserne, der beskriver bevægelsen, er:
-Indledende hastighed veller
-Acceleration til
-Hastighed v
-Oprindelig position xeller
-Position x
-Forskydning Dx
-Vejr t
Alt undtagen tid er vektorer, men da det er en endimensionel bevægelse med en bestemt retning, er det der betyder noget at bruge + eller - tegn til at indikere, hvor størrelsen det drejer sig om. I tilfælde af lodret træk går tyngdekraften altid nedad, og medmindre andet er angivet, tildeles det et tegn -.
Følgende er ligningerne tilpasset lodret træk, der erstatter “x" til "Y"Y"til" til "g”. Derudover inkluderes tegnet (-) svarende til tyngdekraften rettet nedad med det samme:
1) Position: y = yeller + veller.t - ½ g.tto
2) Hastighed: v = veller - g.t
3) Hastighed som en funktion af forskydning ΔY: vto = vellerto - 2 g. ΔY
Nedenfor er anvendelseseksempler til lodret optagelse. I sin beslutning skal følgende tages i betragtning:
-"g”Har en konstant værdi, der i gennemsnit er 9,8 m / sto eller ca. 10 m / sto hvis det foretrækkes for at lette beregningerne, når der ikke kræves for meget præcision.
-Hvornår veller okay 0, disse ligninger reduceres til dem af frit fald.
-Hvis lanceringen er opad, skal objektet have en indledende hastighed, der gør det muligt at bevæge sig. Når den er i bevægelse, når objektet en maksimal højde, der afhænger af, hvor stor starthastigheden er. Jo højere højde, jo mere tid bruger mobilen selvfølgelig i luften.
-Objektet vender tilbage til startpunktet med den samme hastighed, som det blev kastet med, men hastigheden er rettet nedad.
-Ved en lodret start nedad, jo højere starthastighed, jo hurtigere vil objektet ramme jorden. Her indstilles den tilbagelagte afstand i henhold til den valgte højde til lanceringen.
-I det lodrette opadgående kast beregnes den tid, det tager for mobilen at nå den maksimale højde ved at gøre v = 0 i ligning 2) i det foregående afsnit. Dette er maksimal tid tmaks:
0 = veller - g. tmaks ⇒ tmaks = veller / g
-Det maksimal højde Ymaks fjernes fra ligning 3) i det foregående afsnit ved at gøre det samme v = 0:
0 = vellerto - 2 g. Δy ⇒ 0 = vellerto - 2 g. (Ymaks - Yeller) ⇒ ogmaks = ogeller + vellerto / 2 g
Ja Yeller = 0, Det reduceres til:
Ymaks = vellerto / 2 g
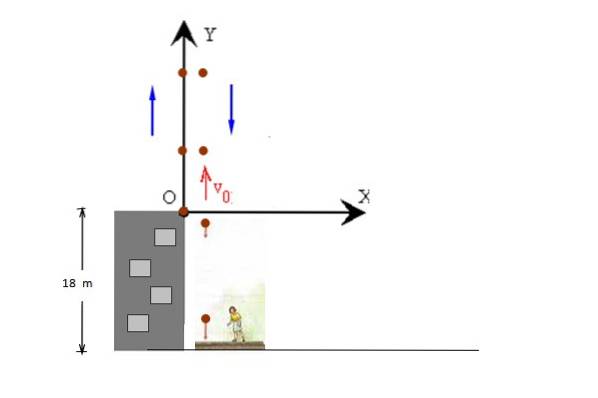
En bold kastes lodret opad med veller = 14 m / s, fra toppen af en 18 m høj bygning. Bolden får lov til at fortsætte sin vej ned til fortovet. Beregn:
a) Den maksimale højde, som bolden har nået i forhold til jorden.
b) Den tid det var i luften (flyvetid).
Figuren viser løfte- og sænkebevægelser af bolden separat for klarhedens skyld, men begge forekommer langs den samme linje. Den oprindelige position tages ved y = 0, så den endelige position er y = - 18 m.
a) Den maksimale højde målt fra bygningens tag er Ymaks = vellerto / 2 g og fra udsagnet kan vi læse, at starthastigheden er +14 m / s, så:
Ymaks = (14 m / s)to / 2 x 9,8 m / sto = 10 m (Med hensyn til taget)
Hmaks = 10 m + 18 m = 28 m (Med hensyn til fortovet).
b) At finde samlet tid eller flyvetid bolden holder i luften, ligningen vil blive brugt y = yeller + veller.t - ½ g.tto, med følgende værdier og tegn:
y = - 18 m
Yeller = 0 m
veller = +14 m / s
Udskiftning:
- 18 = 14.t - ½ 9.8 .tto
- 4,9 tto+14.t + 18 = 0
4,9 tto-14.t - 18 = 0
Det er en ligning af anden grad, der let løses ved hjælp af en videnskabelig lommeregner eller ved hjælp af opløseren. Løsningerne er: 3.82 og -0.96. Den negative løsning kasseres, da den mangler fysisk forstand, da det er en tid.
Boldens flyvetid er 3,82 sekunder.
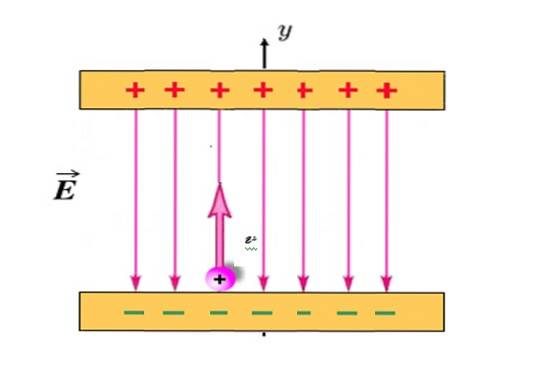
En positivt ladet partikel med q = +1,2 millicoulombs (mC) og masse m = 2,3 x 10 -10 Kg projiceres lodret opad, startende fra positionen vist i figuren og med starthastighed veller = 30 km / s.
Mellem de ladede plader er der et elektrisk felt OG ensartet, lodret lodret nedad og med en størrelse på 780 N / C. Hvis afstanden mellem pladerne er 18 cm, kolliderer partiklen med toppladen? Forsøm tyngdekraften på partiklen, da den er ekstremt lys.
I dette problem det elektriske felt OG er den, der producerer en kraft F og den deraf følgende acceleration. At være positivt ladet, er partiklen altid tiltrukket af den nederste plade, men når den projiceres lodret opad, når den en maksimal højde og vender derefter tilbage til den nederste plade, ligesom kuglen i de foregående eksempler..
Per definition af elektrisk felt:
E = F / q = m.a / q ⇒ a = q.E / m
Du skal bruge denne ækvivalens, inden du udskifter værdier:
1 mC = 1 x 10-3 C
Således er accelerationen:
a = 1,2 x 10-3 x 780 / 2,3 x 10 -10Frkto = 4,07 x 109 Frkto
For den maksimale højde anvendes formlen fra det foregående afsnit, men i stedet for at bruge “g”Denne accelerationsværdi bruges:
Ymaks = vellerto / 2a = (30.000 m / s)to/ 2 x 4,07 x 109 Frkto = 0,11 m = 11 cm
Det kolliderer ikke med den øverste plade, da den er 18 cm fra startpunktet, og partiklen kun når op 11 cm.
Endnu ingen kommentarer