
Isometrisk transformationssammensætning, typer og eksempler

Det isometriske transformationer De er ændringer i placeringen eller orienteringen af en bestemt figur, der ikke ændrer dens form eller størrelse. Disse transformationer er klassificeret i tre typer: translation, rotation og refleksion (isometri). Generelt giver geometriske transformationer dig mulighed for at oprette en ny figur ud fra en given.
En transformation til en geometrisk figur betyder, at den på en eller anden måde har gennemgået en vis ændring; det vil sige, det blev ændret. I henhold til originalen og lignende i planet kan geometriske transformationer klassificeres i tre typer: isometrisk, isomorf og anamorf..

Artikelindeks
- 1 Funktioner
- 2 slags
- 2.1 Ved oversættelse
- 2.2 Ved rotation
- 2.3 Ved refleksion eller symmetri
- 3 Sammensætning
- 3.1 Sammensætning af en oversættelse
- 3.2 Sammensætning af en rotation
- 3.3 Sammensætning af en symmetri
- 4 Referencer
Egenskaber
Isometriske transformationer opstår, når størrelsen af segmenterne og vinklerne mellem den originale figur og den transformerede figur bevares.
I denne type transformation ændres hverken figurens størrelse eller størrelse (de er kongruente), det er kun en ændring i dets position, hverken i retning eller i retning. På denne måde vil de indledende og endelige tal være ens og geometrisk kongruente..
Isometri henviser til lighed; dvs. geometriske figurer vil være isometriske, hvis de har samme form og størrelse.
I isometriske transformationer er det eneste, der kan observeres, en ændring af position i planet, der opstår en stiv bevægelse, takket være hvilken figuren går fra en startposition til en endelig. Denne figur kaldes homolog (lignende) af originalen.
Der er tre typer bevægelser, der klassificerer en isometrisk transformation: translation, rotation og refleksion eller symmetri.
Typer
Ved oversættelse
Det er de isometrier, der tillader, at alle flyets punkter forskydes i en lige linje i en given retning og afstand.
Når en figur transformeres ved oversættelse, ændrer den ikke sin orientering i forhold til den oprindelige position, og den mister heller ikke sine interne mål, målene for dens vinkler og sider. Denne type forskydning er defineret af tre parametre:
- En retning, som kan være vandret, lodret eller skråt.
- En fornemmelse, som kan være venstre, højre, op eller ned.
- Afstand eller størrelse, som er længden fra startpositionen til slutningen af ethvert punkt, der bevæger sig.
For at en isometrisk transformation ved oversættelse skal være opfyldt, skal følgende betingelser være opfyldt:
- Figuren skal altid holde alle dens dimensioner, både lineære og vinklede.
- Figuren ændrer ikke sin position i forhold til den vandrette akse; det vil sige, at dens vinkel aldrig varierer.
- Oversættelserne vil altid blive opsummeret i en enkelt, uanset antallet af oversættelser, der foretages..
I et plan, hvor centrum er et punkt O, med koordinater (0,0), defineres oversættelsen med en vektor T (a, b), der angiver forskydningen af det oprindelige punkt. Nemlig:
P (x, y) + T (a, b) = P '(x + a, y + b)
For eksempel, hvis en oversættelse T (-4, 7) anvendes til koordinatpunktet P (8, -2), får vi:
P (8, -2) + T (-4, 7) = P '[(8 + (-4)), ((-2) + 7)] = P' (4, 5)
I det følgende billede (til venstre) kan det ses, hvordan punkt C bevægede sig sammen med D. Det gjorde det i lodret retning, retningen var opad og afstanden eller størrelses-cd'en var 8 meter. I det rigtige billede ses oversættelsen af en trekant:
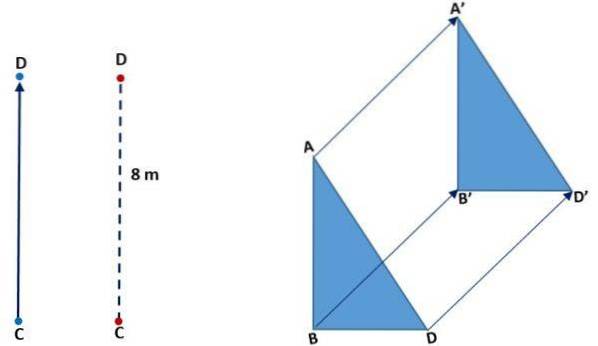
Ved rotation
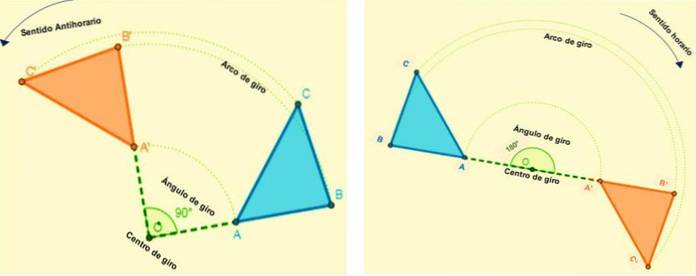
Det er de isometrier, der gør det muligt for figuren at rotere alle punkterne i et plan. Hvert punkt roterer efter en bue, der har en konstant vinkel og et fast punkt (omdrejningspunkt) bestemt.
Det vil sige, al rotation vil blive defineret af dens rotationscenter og rotationsvinkel. Når en figur transformeres ved rotation, holder den målene for dens vinkler og sider.
Rotationen sker i en bestemt retning, den er positiv, når rotationen er mod uret (mod uret) og negativ, når dens rotation er med uret..
Hvis et punkt (x, y) roteres i forhold til oprindelsen - det vil sige, at dets rotationscenter er (0,0) -, med en vinkel på 90eller til 360eller koordinaterne for punkterne vil være:
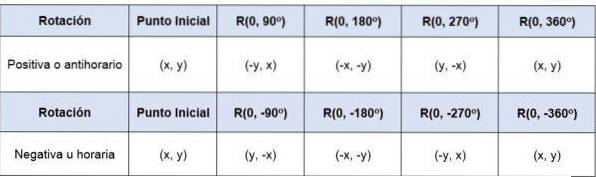
I det tilfælde, hvor rotationen ikke har et centrum ved oprindelsen, skal koordinatsystemets oprindelse overføres til den nye givne oprindelse for at kunne rotere figuren med oprindelsen som centrum..
For eksempel, hvis punktet P (-5,2) drejes 90eller, omkring oprindelsen og i en positiv retning vil dens nye koordinater være (-2,5).
Ved refleksion eller symmetri
Det er de transformationer, der inverterer planens punkter og figurer. Denne inversion kan være med hensyn til et punkt, eller det kan også være med hensyn til en linje.
Med andre ord, i denne type transformation er hvert punkt i den oprindelige figur forbundet med et andet punkt (billede) af den homologe figur på en sådan måde, at punktet og dets billede er i samme afstand fra en linje kaldet aksen af symmetri..
Således vil den venstre del af figuren være en afspejling af den højre del uden at ændre dens form eller dimensioner. Symmetri omdanner en figur til en anden lige, men i den modsatte retning, som det kan ses på følgende billede:
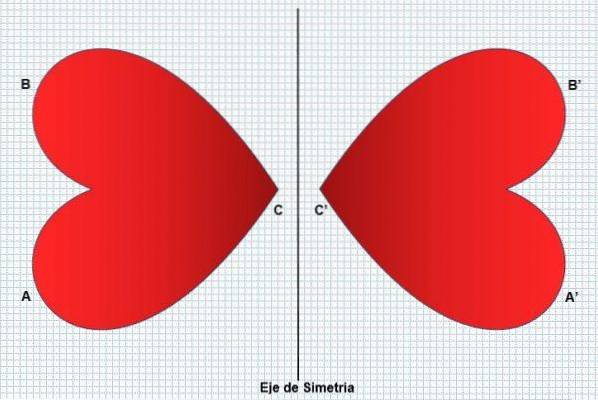
Symmetri er til stede i mange aspekter, såsom i nogle planter (solsikker), dyr (påfugl) og naturfænomener (snefnug). Mennesket reflekterer det på sit ansigt, der betragtes som en skønhedsfaktor. Refleksion eller symmetri kan være af to typer:
Central symmetri
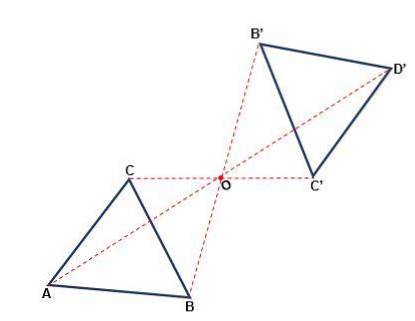
Det er den transformation, der finder sted i forhold til et punkt, hvor figuren kan ændre sin orientering. Hvert punkt i den originale figur og dets billede er i samme afstand fra et punkt O, kaldet centrum for symmetri. Symmetri er central, når:
- Både punktet og dets billede og centrum hører til den samme linje.
- Med en rotation på 180eller fra centrum O opnås et tal svarende til originalen.
- Slagene fra den oprindelige figur er parallelle med slagene fra den dannede figur.
- Følelsen af figuren ændres ikke, den vil altid være med uret.
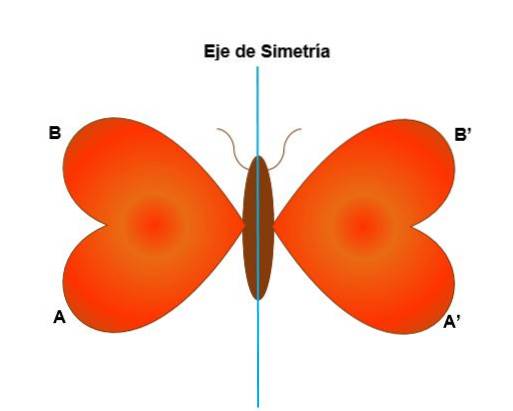
Denne transformation sker med hensyn til symmetriaksen, hvor hvert punkt i den oprindelige figur er forbundet med et andet punkt i billedet, og disse er i samme afstand fra symmetriaksen. Symmetri er aksial, når:
- Det segment, der forbinder et punkt med dets billede, er vinkelret på symmetriaksen.
- Figurerne skifter retning i forhold til rotation eller med uret.
- Når figuren deles med en central linje (symmetriakse), falder en af de resulterende halvdele helt sammen med en anden af halvdelene.
Sammensætning
En sammensætning af isometriske transformationer henviser til den successive anvendelse af isometriske transformationer på den samme figur.
Sammensætning af en oversættelse
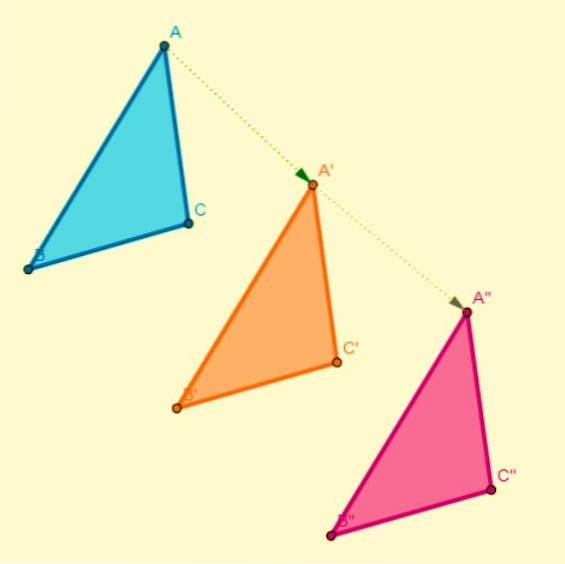
Sammensætningen af to oversættelser resulterer i en anden oversættelse. Når den udføres på planet, ændres kun aksens koordinater på den vandrette akse (x), mens koordinaterne for den lodrette akse (y) forbliver de samme, og omvendt.
Sammensætning af en rotation
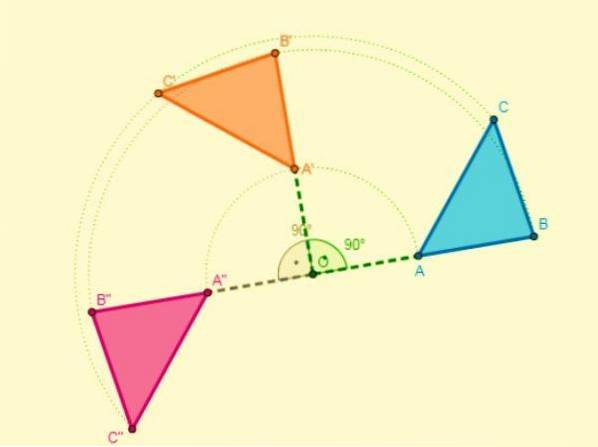
Sammensætningen af to drejninger med det samme center resulterer i en anden drejning, der har det samme centrum, og hvis amplitude vil være summen af amplituden af de to drejninger..
Hvis omdrejningens centrum har et andet center, vil skæringen af halveringen af to segmenter af lignende punkter være omdrejningspunktet.
Sammensætning af en symmetri
I dette tilfælde afhænger sammensætningen af, hvordan den anvendes:
- Hvis den samme symmetri anvendes to gange, bliver resultatet en identitet.
- Hvis der anvendes to symmetrier i forhold til to parallelle akser, bliver resultatet en oversættelse, og dens forskydning er dobbelt så langt fra disse akser:
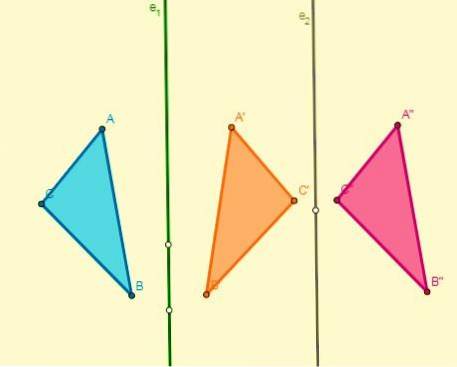
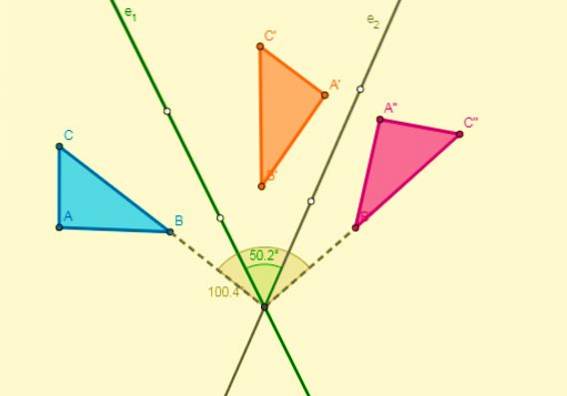
- Hvis der anvendes to symmetrier i forhold til to akser, der krydser hinanden ved punkt O (centrum), opnås en rotation med centrum ved O, og dens vinkel vil være dobbelt så stor som vinklen, som akserne dannes:
Referencer
- V Burgués, J. F. (1988). Materialer til konstruktion af geometri. Madrid: Syntese.
- Cesar Calavera, I. J. (2013). Teknisk tegning II. Paraninfo S.A: Editions of the Tower.
- Coxeter, H. (1971). Grundlæggende om geometri. Mexico: Limusa-Wiley.
- Coxford, A. (1971). Geometri En transformationsmetode. USA: Laidlaw Brothers.
- Liliana Siñeriz, R. S. (2005). Induktion og formalisering i undervisningen i stive transformationer i CABRI-miljøet.
- , P. J. (1996). Gruppen af isometrier af flyet. Madrid: Syntese.
- Suárez, A.C. (2010). Transformationer i flyet. Gurabo, Puerto Rico: AMCT .



Endnu ingen kommentarer