
Fourier transform egenskaber, applikationer, eksempler
Det Fourier-transformation er en metode til analytisk tilstrækkelighed orienteret om integrerbare funktioner, der hører til familien af tintegreret transformeret. Den består af en omdefinering af funktioner F (t) med hensyn til Cos (t) og Sen (t).
De trigonometriske identiteter af disse funktioner sammen med deres aflednings- og antideriveringsegenskaber tjener til at definere Fourier-transformationen gennem følgende komplekse funktion:
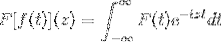
Hvilket er sandt, så længe udtrykket giver mening, det vil sige når det ukorrekte integral er konvergent. Algebraisk siges Fourier-transformationen at være en lineær homeomorfisme.
Hver funktion, der kan arbejdes med en Fourier-transformation, skal præsentere null uden for en defineret parameter.
Artikelindeks
- 1 egenskaber
- 1.1 Eksistens
- 1.2 Lineæritet af Fourier-transformation
- 1.3 Fouriertransformation af et derivat
- 1.4 Differentiering af Fourier-transformationen
- 1.5 Fourier-transformation af en oversættelse
- 1.6 Oversættelse af Fourier-transformationen
- 1.7 Fouriertransformation af en skalagruppe
- 1.8 Symmetri
- 1.9 Fouriertransformation af et kollisionsprodukt
- 1.10 Kontinuitet og henfald til uendelig
- 2 Historie
- 3 Hvad er Fourier-transformationen til?
- 3.1 Fourier-serien
- 3.2 Andre former for Fourier-serien
- 4 applikationer
- 4.1 Beregning af den grundlæggende løsning
- 4.2 Signalteori
- 5 eksempler
- 5.1 Eksempel 1
- 5.2 Eksempel 2
- 6 Foreslåede øvelser
- 7 Referencer
Ejendomme

Fourier-transformen opfylder følgende egenskaber:
Eksistens
At verificere eksistensen af Fouriertransformationen i en funktion f (t) defineret i realerne R, følgende 2 aksiomer skal være opfyldt:
- f (t) er stykkevis kontinuerlig for alt R
- f (t) er integrerbar i R
Fourier transformation linearitet
Lad M (t) og N (t) være to funktioner med bestemte Fourier-transformationer, med alle konstanter a og b.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Hvilket også understøttes af lineariteten af integralen med samme navn.
Fourier-transformation af et derivat
Det har en funktion F som er kontinuerlig og integrerbar i alle realiteter, hvor:
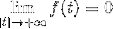
Og afledte af f (f ') er kontinuerlig og defineret stykkevis igennem R
Fourier-transformationen af et derivat defineres ved integration af dele ved følgende udtryk:
F [f '(t)] (z) = izF [f (t)] (z)
I afledninger af højere orden vil den blive anvendt på en homolog måde, hvor vi for alle n 1 har:
F [f n'(t)] (z) = (iz)nF [f (t)] (z)
Fourier transform differentiering
Det har en funktion F som er kontinuerlig og integrerbar i alle realiteter, hvor:
i (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Fourier-transformation af en oversættelse
For alle θ som hører til et sæt S og T som hører til sættet S ', har vi:
F [ τtil θ] = og-iay F [ θ] F [ τtilT ] = og-iax F [ T]
Med τtil arbejder som oversættelsesoperatør på vektoren a.
Oversættelse af Fourier-transformationen
For alle θ som hører til et sæt S og T som hører til sættet S ', har vi:
τtil F [θ] = F [og-iax.θ] τtil F [T ] = F [og-iay . T]
For alle til som hører til R
Fourier-transformation af en skala gruppe
For alle θ som hører til et sæt S. T som hører til sættet S '
λ tilhører R - 0 du skal:
F [θ (λx)] = (1 / | λ |) F [θ] (Y /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / λ)
Ja F er en kontinuerlig og tydeligt integrerbar funktion, hvor a> 0. Derefter:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
For at demonstrere dette resultat kan vi fortsætte med ændringen af variablen.
Når T → + så er s = ved → + ∞
Når T → - så er s = ved → - ∞
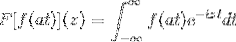
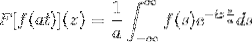
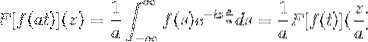
Symmetri
For at studere symmetrien af Fourier-transformationen skal identiteten af Parseval og Plancherel-formlen verificeres.
Vi har θ og δ, der hører til S. Derfra kan det udledes, at:
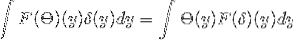
Kom
1 / (2π)d F [θ ], F [δ] Parsevals identitet
1 / (2π)d / 2 || F [θ ] ||LtoRd Plancherel formel
Fourier-transformation af et kollisionsprodukt
Ved at forfølge lignende mål som i Laplace-transformen henviser sammensmeltning af funktioner til produktet mellem deres Fourier-transformationer.
Vi har f og g som 2 afgrænsede, bestemte og fuldstændigt integrerbare funktioner:
F (f * g) = F (f). F (g)
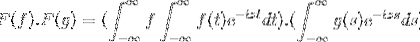
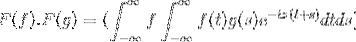
Derefter når du ændrer variablen
t + s = x; det fortsætter med den forkerte dobbelte integral
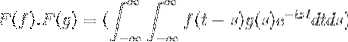
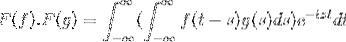
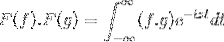
F (f). F (g) = F (f. G)
Kontinuitet og falder i uendelighed
For alle θ som hører til R, F [ θ] overholder kriterierne for en kontinuerlig funktion afgrænset i Rd.
Også F [ θ] (y) → 0 i C, hvis | y | → ∞
Historie
Dette matematiske koncept blev præsenteret af Joseph B. Fourier i 1811, mens han udviklede en afhandling om varmespredning. Det blev hurtigt vedtaget af forskellige grene inden for videnskab og teknik.
Det blev etableret som det vigtigste arbejdsredskab i studiet af ligninger med delvise derivater, endda sammenlignet med det eksisterende arbejdsforhold mellem Laplace-transformation og almindelige differentialligninger.
Hvad er Fourier-transformationen til?
Det tjener primært til at forenkle ligninger betydeligt, samtidig med at afledte udtryk omdannes til magtelementer, hvilket betegner differentielle udtryk i form af integrerbare polynomer..
I optimering, modulering og modellering af resultater fungerer det som et standardiseret udtryk og er en hyppig ressource til teknik efter flere generationer.
Fourier-serien
De er serier defineret i form af Cosines og Sines; De tjener til at lette arbejdet med generelle periodiske funktioner. Når de anvendes, er de en del af teknikkerne til løsning af almindelige og delvise differentialligninger..
Fourier-serien er endnu mere generel end Taylor-serien, fordi de udvikler periodiske diskontinuerlige funktioner, der ikke har en Taylor-serierepræsentation..
Andre former for Fourier-serien
For at forstå Fourier-transformationen analytisk er det vigtigt at gennemgå de andre måder, hvorpå Fourier-serien kan findes, indtil vi kan definere Fourier-serien i dens komplekse notation.
-Fourier-serier på en 2L periode-funktion
Mange gange er det nødvendigt at tilpasse strukturen i en Fourier-serie til periodiske funktioner, hvis periode er p = 2L> 0 i intervallet [-L, L].
-Fourier-serier i ulige og lige funktioner
Intervallet [-π, π] betragtes, hvilket giver fordele, når man udnytter funktionernes symmetriske egenskaber.
Hvis f er jævn, etableres Fourier-serien som en serie Cosines.
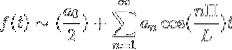
Hvis f er ulige, etableres Fourier-serien som en serie af Sines.
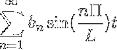
-Kompleks notation af Fourier-serien
Hvis vi har en funktion f (t), der opfylder alle udviklingsbarhedskravene i Fourier-serien, er det muligt at angive den i intervallet [-t, t] ved hjælp af dens komplekse notation:
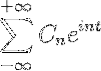
Ansøgninger

Beregning af den grundlæggende løsning
Fouriertransformationen er et kraftfuldt værktøj til undersøgelse af delvise differentialligninger af den lineære type med konstante koefficienter. De gælder ligeledes for funktioner med ubegrænsede domæner.
Ligesom Laplace-transformationen forvandler Fourier-transformationen en delvis afledt funktion til en almindelig differentialligning, der er meget lettere at betjene..
Cauchy-problemet for varmeligningen præsenterer et felt med hyppig anvendelse af Fourier-transformen, hvor funktionen genereres varmekerne eller Dirichlet-kerne.
Med hensyn til beregningen af den grundlæggende løsning præsenteres følgende tilfælde, hvor det er almindeligt at finde Fourier-transformationen:
-Laplace ligning
-Varmeligning
-Schrödinger ligning
-Bølge ligning
Signal teori
Den generelle årsag til anvendelsen af Fourier-transformen i denne gren skyldes hovedsageligt den karakteristiske nedbrydning af et signal som en uendelig superposition af lettere behandlingsbare signaler.
Det kan være en lydbølge eller en elektromagnetisk bølge, Fourier-transformationen udtrykker den i en superposition af enkle bølger. Denne repræsentation er ret hyppig inden for elektroteknik.
På den anden side er der eksempler på anvendelse af Fourier-transform inden for signalteori:
-Problemer med systemidentifikation. Etableret f og g
-Problem med udgangssignalkonsistens
-Problemer med signalfiltrering
Eksempler
Eksempel 1
Definer Fourier-transformationen til følgende udtryk:
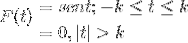
Vi kan også repræsentere det på følgende måde:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
Den rektangulære puls er defineret:
p (t) = H(t + k) - H(t - k)
Fourier-transformen anvendes til det følgende udtryk, der ligner moduleringssætningen.
f (t) = p (t) Sen (t)
Hvor: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Og Fourier-transformeringen er defineret af:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Eksempel 2
Definer Fourier-transform til udtrykket:
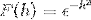
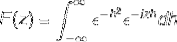
Da f (h) er en jævn funktion, kan det siges, at
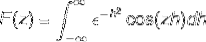
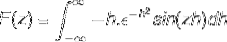
Integration af dele anvendes ved at vælge variablerne og deres forskelle som følger
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)to v = (e-h)to / to
Udskiftning har du
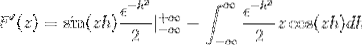
Efter evaluering under den grundlæggende sætning af beregning
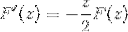
Ved anvendelse af forudgående viden om førsteordens differentialligninger betegnes udtrykket som
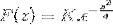
For at opnå K vurderer vi
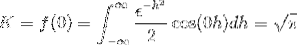
Endelig er Fourier-transformationen af udtrykket defineret som
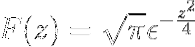
Foreslåede øvelser
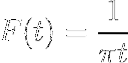
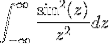
- Få transformationen af udtrykket W / (1 + wto)
Referencer
- Duoandikoetxea Zuazo, J., Fourier-analyse. Addison- Wesley Iberoamericana, Autonome Universitet i Madrid, 1995.
- Lions, J. L., matematisk analyse og numeriske metoder til videnskab og teknologi. Springer-Verlag, 1990.
- Lieb, E. H., Gaussiske kerner har kun gaussiske maksimeringer. Opfind. Matematik. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier Series og Integrals. Academic Press, New York, 1972.
- Schwartz, L., Théorie des Distributions. Ed. Hermann, Paris, 1966.



Endnu ingen kommentarer