
Laplace transformerer definition, historie og hvad den er til
Det Laplace-transformation I de senere år har det været af stor betydning inden for ingeniør-, matematik- og fysikstudier, blandt andre videnskabelige områder, da det ud over at være af stor teoretisk interesse giver en enkel måde at løse problemer, der kommer fra videnskab og teknik..
Oprindeligt blev Laplace-transformen præsenteret af Pierre-Simón Laplace i sin undersøgelse af sandsynlighedsteori og blev oprindeligt behandlet som et matematisk objekt af rent teoretisk interesse..

Nuværende applikationer opstår, når forskellige matematikere forsøgte at give en formel begrundelse for de "operationelle regler", der blev brugt af Heaviside i studiet af ligninger af elektromagnetisk teori..
Artikelindeks
- 1 Definition
- 1.1 Eksempler
- 1.2 Sætning (tilstrækkelige betingelser for eksistens)
- 1.3 Laplace-transformation af nogle grundlæggende funktioner
- 2 Historie
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 egenskaber
- 3.1 Lineæritet
- 3.2 Første oversættelsessætning
- 3.3 Anden oversættelsessætning
- 3.4 Skalaændring
- 3.5 Laplace's transformation af derivater
- 3.6 Laplace-transformation af integraler
- 3.7 Multiplikation med tn
- 3.8 Opdeling efter t
- 3.9 Periodiske funktioner
- 3.10 Opførsel af F (s) som s har tendens til uendelig
- 4 Inverse transformationer
- 4.1 Øvelse
- 5 Anvendelser af Laplace-transform
- 5.1 Differentialligninger
- 5.2 Systemer med differentialligninger
- 5.3 Mekanik og elektriske kredsløb
- 6 Referencer
Definition
Lad f være en funktion defineret for t ≥ 0. Laplace-transformationen er defineret som følger:
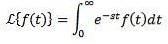
Laplace-transformationen siges at eksistere, hvis den tidligere integral konvergerer, ellers siges det, at Laplace-transformationen ikke eksisterer.
Generelt bruges små bogstaver til at betegne den funktion, der skal transformeres, og det store bogstav svarer til dets transformation. På denne måde vil vi have:
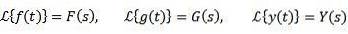
Eksempler
Overvej den konstante funktion f (t) = 1. Vi har, at dens transformation er:
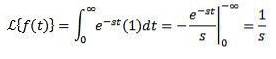
Når integralet konvergerer, er det når s> 0. Ellers er s < 0, la integral diverge.
Lad g (t) = t. Dens Laplace-transformation er givet af
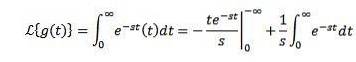
Ved at integrere med dele og vide, at du-St. har tendens til 0 når tendens til uendelighed og s> 0 sammen med det foregående eksempel har vi:
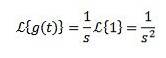
Transformationen eksisterer måske eller måske ikke, for eksempel for funktionen f (t) = 1 / t integrerer ikke integralet, der definerer sin Laplace-transformation, og derfor findes dens transformation ikke.
De tilstrækkelige betingelser for at garantere, at Laplace-transformationen af en funktion f eksisterer, er at f er kontinuerlig i dele for t ≥ 0 og er i eksponentiel rækkefølge.
En funktion siges at være stykkevis kontinuerlig for t ≥ 0, når der for et hvilket som helst interval [a, b] med a> 0 er der et endeligt antal punkter tk, hvor f har diskontinuiteter og er kontinuerligt i hvert underinterval [tk-1,tk].
På den anden side siges det, at en funktion er af eksponentiel rækkefølge c, hvis der er reelle konstanter M> 0, c og T> 0 således, at:
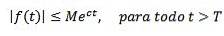
Som eksempler har vi, at f (t) = tto er af eksponentiel rækkefølge, da | tto| < e3t for alle t> 0.
På en formel måde har vi følgende sætning
Sætning (tilstrækkelige betingelser for eksistens)
Hvis f er en delkontinuerlig funktion for t> 0 og af eksponentiel rækkefølge c, eksisterer der Laplace-transformationen for s> c.
Det er vigtigt at bemærke, at dette er en betingelse for tilstrækkelighed, dvs. det kan være tilfældet, at der er en funktion, der ikke opfylder disse betingelser, og alligevel eksisterer dens Laplace-transformation.
Et eksempel på dette er funktionen f (t) = t-1/2 som ikke er stykkevis kontinuerlig for t ≥ 0, men dens Laplace-transformation eksisterer.
Laplace-transformation af nogle grundlæggende funktioner
Følgende tabel viser Laplace-transformationer af de mest almindelige funktioner.

Historie
Laplace-transformationen skylder sit navn Pierre-Simon Laplace, en fransk matematiker og teoretisk astronom, der blev født i 1749 og døde i 1827. Hans berømmelse var sådan, at han var kendt som Newton i Frankrig.
I 1744 viet Leonard Euler sine studier til integraler med formularen
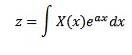
som løsninger på almindelige differentialligninger, men han opgav hurtigt denne undersøgelse. Senere undersøgte Joseph Louis Lagrange, der i høj grad beundrede Euler, også denne type integraler og relaterede dem til sandsynlighedsteori.
1782, Laplace
I 1782 begyndte Laplace at studere disse integraler som løsninger på differentialligninger, og ifølge historikere besluttede han i 1785 at omformulere problemet, som senere gav anledning til Laplace-transformationer, som de forstås i dag..
Efter at være blevet introduceret inden for sandsynlighedsteorien, var det af ringe interesse for datidens videnskabsmænd og blev kun set som et matematisk objekt af kun teoretisk interesse..
Oliver Heaviside
Det var i midten af det 19. århundrede, da den engelske ingeniør Oliver Heaviside opdagede, at differentielle operatører kan behandles som algebraiske variabler, hvilket giver Laplace transformerer deres moderne anvendelse..
Oliver Heaviside var en engelsk fysiker, elektroingeniør og matematiker, der blev født i London i 1850 og døde i 1925. Mens han forsøgte at løse differentialligningsproblemer anvendt på vibrationsteori og ved hjælp af Laplaces studier, begyndte han at forme de moderne anvendelser af Laplace-transformer..
De resultater, der blev præsenteret af Heaviside spredte sig hurtigt i hele det videnskabelige samfund, men da hans arbejde ikke var stringent, blev han hurtigt kritiseret af de mere traditionelle matematikere..
Imidlertid anvendte Heavisides arbejde med at løse ligninger i fysik hans metoder populære hos fysikere og ingeniører..
På trods af disse tilbageslag og efter et par årtier med mislykkede forsøg kunne der i begyndelsen af det 20. århundrede gives en streng begrundelse for de operationelle regler, som Heaviside gav..
Disse forsøg bar frugt takket være forskellige matematikers indsats som Bromwich, Carson, van der Pol, blandt andre..
Ejendomme
Blandt egenskaberne ved Laplace-transformationen skiller sig følgende ud:
Lineæritet
Lad c1 og c2 være konstant, og f (t) og g (t) -funktioner, hvis Laplace-transformationer er henholdsvis F (s) og G (s), så har vi:
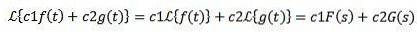
På grund af denne egenskab siges Laplace-transformation at være en lineær operator.
Eksempel
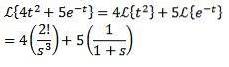
Første oversættelse sætning
Hvis det sker, at:
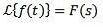
Og 'a' er et hvilket som helst reelt tal, så:
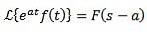
Eksempel
Da Laplace-transformationen af cos (2t) = s / (s ^ 2 + 4), så:
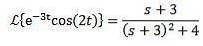
Anden oversættelse sætning
Ja
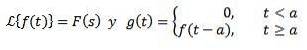
Derefter
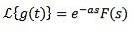
Eksempel
Hvis f (t) = t ^ 3, så er F (s) = 6 / s ^ 4. Og derfor transformationen af
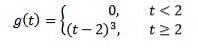
er G (s) = 6e-2s/ s ^ 4
Skalaændring
Ja
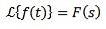
Og 'a' er en ikke-nul reel, det skal vi
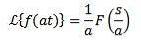
Eksempel
Da transformationen af f (t) = sin (t) er F (s) = 1 / (s ^ 2 + 1) har vi
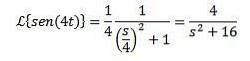
Laplace-transformation af derivater
Hvis f, f ', f ",…, f(n) er kontinuerlige for t ≥ 0 og er af eksponentiel rækkefølge og f(n)(t) er derefter stykkevis kontinuerlig for t ≥ 0, derefter
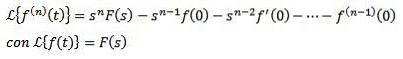
Laplace-transformation af integraler
Ja
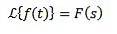
Derefter
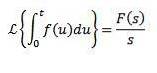
Multiplikation med tn
Hvis vi skal
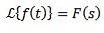
Derefter
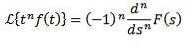
Opdeling efter t
Hvis vi skal
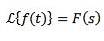
Derefter
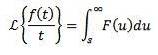
Periodiske funktioner
Lad f være en periodisk funktion med periode T> 0, det vil sige f (t + T) = f (t), så
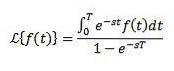
Opførsel af F (s) som s har tendens til uendelig
Hvis f er kontinuerlig i dele og i eksponentiel rækkefølge og
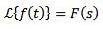
Derefter
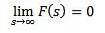
Inverse transformationer
Når vi anvender Laplace-transformationen til en funktion f (t) opnår vi F (s), som repræsenterer nævnte transformation. På samme måde kan vi sige, at f (t) er den inverse Laplace-transformation af F (s) og er skrevet som
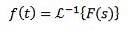
Vi ved, at Laplace-transformationerne af f (t) = 1 og g (t) = t er F (s) = 1 / s og G (s) = 1 / sto henholdsvis derfor skal vi
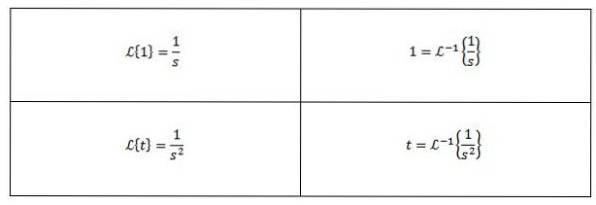
Nogle almindelige inverse Laplace-transformationer er som følger

Desuden er den omvendte Laplace-transformation lineær, det vil sige det
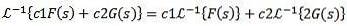
Dyrke motion
Finde
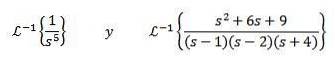
For at løse denne øvelse skal vi matche funktionen F (s) med en af den foregående tabel. I dette tilfælde, hvis vi tager n + 1 = 5 og bruger den inverse transformations linearitetsegenskab, multiplicerer vi og deler med 4! Kom
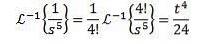
For den anden inverse transformation anvender vi delbrøker for at omskrive funktionen F (s) og derefter egenskaben af linearitet, hvilket opnår
Som vi kan se fra disse eksempler, er det almindeligt, at funktionen F (s), der evalueres, ikke nøjagtigt matcher nogen af funktionerne i tabellen. I disse tilfælde er det som det ses nok at omskrive funktionen, indtil den når den rette form.
Anvendelser af Laplace-transform
Differentialligninger
Den primære anvendelse af Laplace-transformationer er at løse differentialligninger.
Ved hjælp af transformeringsegenskaben for et derivat er det klart, at
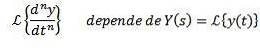
Og af n-1-derivaterne evalueret ved t = 0.
Denne egenskab gør transformationen meget nyttig til løsning af indledende værdiproblemer, hvor differentialligninger med konstante koefficienter er involveret..
De følgende eksempler viser, hvordan man bruger Laplace-transformen til at løse differentialligninger.
Eksempel 1
Givet følgende indledende værdiproblem
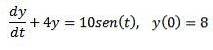
Brug Laplace-transformationen til at finde løsningen.
Vi anvender Laplace-transformationen på hvert medlem af differentialligningen
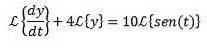
Ved egenskaben til transformationen af et derivat, vi har
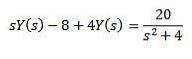
Ved at udvikle alt udtryk og rydde Y (er) er vi tilbage
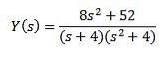
Brug af delvise brøker til at omskrive højre side af ligningen, vi får
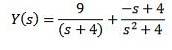
Endelig er vores mål at finde en funktion y (t), der opfylder differentialligningen. Brug af den inverse Laplace-transformation giver os resultatet
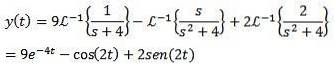
Eksempel 2
Løse
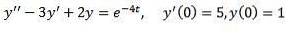
Som i det foregående tilfælde anvender vi transformationen på begge sider af ligningen og adskiller udtryk for udtryk.
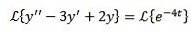
På denne måde har vi som et resultat
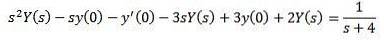
Erstatning med de givne startværdier og løsning af Y (er)
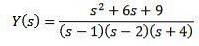
Ved hjælp af enkle brøker kan vi omskrive ligningen som følger
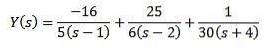
Og anvendelse af den inverse Laplace-transformation giver os resultatet
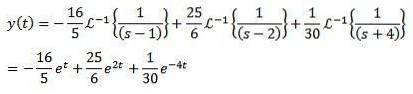
I disse eksempler kunne du komme til den forkerte konklusion, at denne metode ikke er meget bedre end traditionelle metoder til løsning af differentialligninger..
Fordelene ved Laplace-transformationen er, at du ikke behøver at bruge parametervariation eller bekymre dig om de forskellige tilfælde af den ubestemte koefficientmetode..
Derudover, når vi løser startværdiproblemer ved denne metode, bruger vi fra begyndelsen de oprindelige betingelser, så det er ikke nødvendigt at udføre andre beregninger for at finde den bestemte løsning.
Systemer med differentialligninger
Laplace-transformationen kan også bruges til at finde løsninger på samtidige almindelige differentialligninger, som det følgende eksempel viser.
Eksempel
Sorter ud
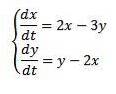
Med de oprindelige betingelser x (0) = 8 og y (0) = 3.
Hvis vi skal
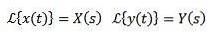
Derefter
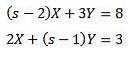
Løsning giver os som et resultat
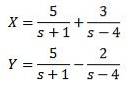
Og anvendelse af den omvendte Laplace-transformation, vi har
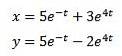
Mekanik og elektriske kredsløb
Laplace-transformationen er af stor betydning i fysik, den har hovedsagelig applikationer til mekanik og elektriske kredsløb.
Et simpelt elektrisk kredsløb består af følgende elementer
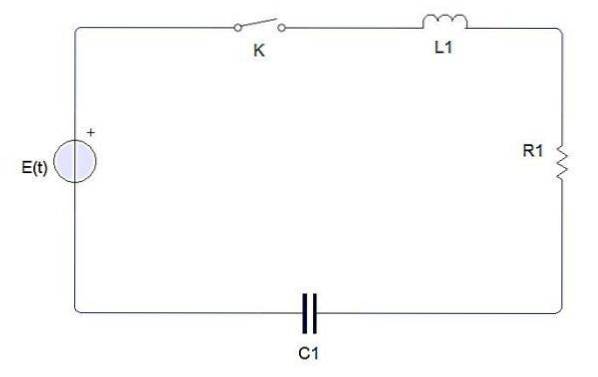
En afbryder, et batteri eller en kilde, en induktor, en modstand og en kondensator. Når kontakten er lukket, produceres en elektrisk strøm, der betegnes med i (t). Kondensatorladningen er betegnet med q (t).
Ved Kirchhoffs anden lov skal spændingen produceret af kilden E til det lukkede kredsløb være lig med summen af hver af spændingsfaldene.
Den elektriske strøm i (t) er relateret til opladningen q (t) på kondensatoren ved i = dq / dt. På den anden side defineres spændingsfaldet i hvert af elementerne som følger:
Spændingsfaldet over en modstand er iR = R (dq / dt)
Spændingsfaldet over en induktor er L (di / dt) = L (dtoq / dtto)
Spændingsfaldet over en kondensator er q / C.
Med disse data og anvendelse af Kirchhoffs anden lov til det enkle lukkede kredsløb opnås en andenordens differentialligning, der beskriver systemet og giver os mulighed for at bestemme værdien af q (t).
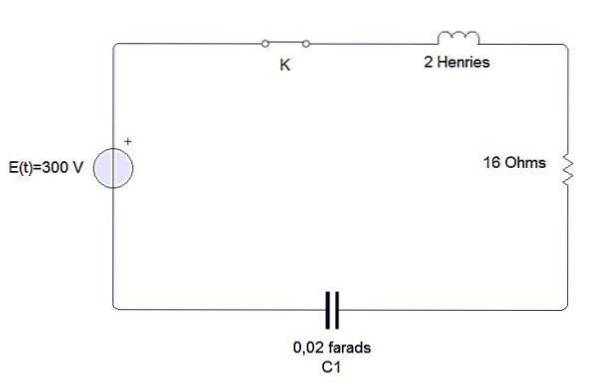
Eksempel
En induktor, en kondensator og en modstand er forbundet til et batteri E, som vist i figuren. Spolen er 2 henries, kondensatoren er 0,02 farads og modstanden er 16 ohm. På tidspunktet t = 0 er kredsløbet lukket. Find opladningen og strømmen til enhver tid t> 0, hvis E = 300 volt.
Vi har, at den differentielle ligning, der beskriver dette kredsløb, er følgende
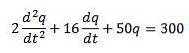
Hvor de oprindelige betingelser er q (0) = 0, i (0) = 0 = q '(0).
Anvendelse af Laplace-transformationen får vi det
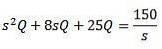
Og løsning for Q (t)
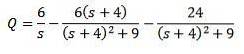
Derefter anvender vi den omvendte Laplace-transformation, vi har
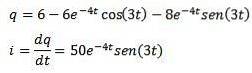
Referencer
- G. Holbrook, J. (1987). Laplace-transformation til elektronikingeniører. Limusa.
- Ruiz, L. M., & Hernandez, M. P. (2006). Differentialligninger og Laplace transformeres med applikationer. Redaktionel UPV.
- Simmons, G. F. (1993). Differentialligninger med applikationer og historiske noter. McGraw-Hill.
- Spiegel, M. R. (1991). Laplace transformerer. McGraw-Hill.
- Zill, D. G., og Cullen, M. R. (2008). Differentialligninger med problemer med grænseværdier. Cengage Learning Editores, S.A.

Endnu ingen kommentarer