
Højre trapezoid egenskaber, relationer og formler, eksempler
EN rektangel trapesformet er en flad figur med fire sider, således at to af dem er parallelle med hinanden, kaldet baser og også en af de andre sider er vinkelret på baserne.
Af denne grund er to af de indvendige vinkler rigtige, dvs. de måler 90º. Deraf navnet "rektangel" givet til figuren. Følgende billede af en højre trapezform præciserer disse egenskaber:
Artikelindeks
- 1 Elementer af trapezformet
- 2 Forhold og formler
- 2.1 Trapezens højde h
- 2.2 Perimeter P
- 2.3 Gennemsnitlig base
- 2.4 Område
- 2.5 Diagonaler, sider og vinkler
- 3 Eksempler på højre trapezoider
- 3.1 Trapesformet som designelement
- 3.2 Trapezformet bølgenerator
- 3.3 I numerisk beregning
- 3.4 Bjælke med trapesformet belastning
- 3.5 Som et uddannelses- og læringsredskab
- 4 Løst øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 5 Referencer
Elementer af trapezformet
Elementerne i trapezformet er:
-Baser
-Hjørner
-Højde
-Indvendige vinkler
-Mellemgrund
-Diagonaler
Vi vil detaljerede disse elementer ved hjælp af figur 1 og 2:
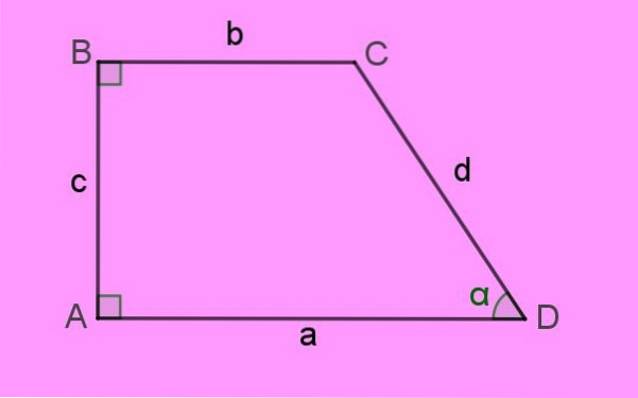
Siderne af højre trapez er betegnet med små bogstaver a, b, c og d. Hjørnerne på figuren o hjørner De er angivet med store bogstaver. Endelig indre vinkler De udtrykkes med græske bogstaver.
Per definition, baser af denne trapez er siderne a og b, som, som det kan ses, er parallelle og også har forskellige længder.
Den side, der er vinkelret på begge baser, er siden c til venstre, som er højde h af trapesen. Og endelig er der siden d, som danner den spidse vinkel α med siden a.
Summen af indre vinkler af en firkant er 360º. Det er let at forstå, at den manglende vinkel C i figuren er 180 - α.
Det midterste base er segmentet, der forbinder midtpunkterne for de ikke-parallelle sider (segment EF i figur 2).
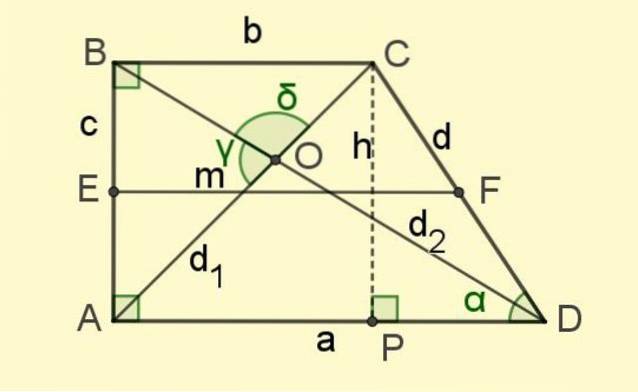
Og endelig er der diagonalerne d1 og dto, segmenterne, der forbinder de modsatte hjørner og skærer hinanden ved punkt O (se figur 2).
Forhold og formler
Trapesformet højde h
h = c
Omkreds P
Det er målingen for konturen og beregnes ved at tilføje siderne:
Perimeter = a + b + c + d
Siden d udtrykkes i form af højden eller siden c ved hjælp af Pythagoras sætning:
d = √ (a-b)to + cto
Udskiftning i omkredsen:
P = a + b + c + √ (a-b)to + cto
Mellemgrund
Det er semisummen af baserne:
Middelbase = (a + b) / 2
Undertiden findes den gennemsnitlige base udtrykt på denne måde:
Gennemsnitlig base = (Major base + mindre base) / 2
Areal
Trapezens område A er produktet af den gennemsnitlige basis gange højden:
A = (Major base + mindre base) x højde / 2
A = (a + b) c / 2
Diagonaler, sider og vinkler
Flere trekanter vises i figur 2, både højre og ikke-rigtige. Pythagoras sætning kan anvendes på dem, der er rigtige trekanter, og på dem, der ikke er det, cosinus- og sinussætningerne.
På denne måde findes relationer mellem siderne og mellem siderne og trapezens indre vinkler..
CPA-trekant
Det er et rektangel, dets ben er ens og er værd at b, mens hypotenusen er den diagonale d1, Dermed:
d1to = bto + bto = 2bto
DAB-trekant
Det er også et rektangel, benene er til Y c (eller også til Y h) og hypotenusen er dto, så det:
dtoto = ato + cto = ato + hto
CDA trekant
Da denne trekant ikke er en rigtig trekant, anvendes cosinus sætningen på den, eller også sinus sætningen.
Ifølge cosinus sætningen:
d1to = ato + dto - 2ad cos α
CDP-trekant
Denne trekant er en ret trekant og med dens sider er de trigonometriske forhold mellem vinklen α konstrueret:
sin α = h / d
cos α = PD / d
Men siden PD = a - b, derfor:
cos α = (a-b) / d → a - b = d cos α
a = b + d cos α
Du har også:
tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)
CBD trekant
I denne trekant har vi den vinkel, hvis toppunkt er ved C. Det er ikke markeret i figuren, men i starten blev det fremhævet, at det er 180 - α. Denne trekant er ikke en rigtig trekant, så cosinus sætning eller sinus sætning kan anvendes..
Nu kan det let vises, at:
sin (180 - α) = sin α
cos (180 - α) = - cos α
Anvendelse af cosinus sætning:
dtoto = dto + bto - 2db cos (180 - α) = dto + bto + 2db cos α
Eksempler på højre trapezoider
Trapezoider og især rigtige trapezoider findes på mange sider og undertiden ikke altid i håndgribelig form. Her har vi flere eksempler:
Trapesformet som designelement
Geometriske figurer bugner af arkitekturen i mange bygninger, såsom denne kirke i New York, der viser en struktur i form af et rektangulært trapesform.
Ligeledes er den trapezformede form hyppig i designet af containere, containere, knive (fræser eller eksakt), badges og i grafisk design.

Trapesformet bølgenerator
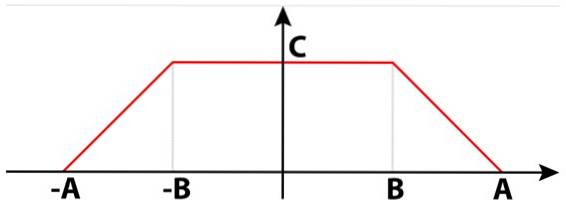
Elektriske signaler kan ikke kun være firkantede, sinusformede eller trekantede. Der er også trapezformede signaler, der er nyttige i mange kredsløb. I figur 4 er der et trapezformet signal sammensat af to højre trapezoider. Mellem dem danner de en enkelt ligebenet trapez.
I numerisk beregning
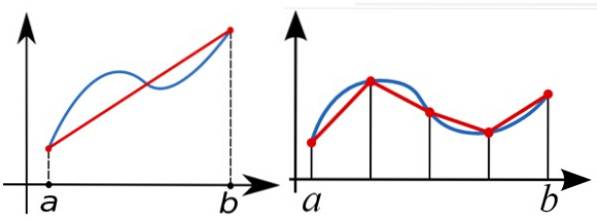
For at beregne den bestemte integral af funktionen f (x) mellem a og b numerisk anvendes trapezreglen til at tilnærme området under grafen for f (x). I den følgende figur er integralet til venstre tilnærmet med en enkelt højre trapez.
En bedre tilnærmelse er den i den rigtige figur med flere højre trapezoider.
Trapesformet bjælke
Styrker er ikke altid koncentreret om et enkelt punkt, da de kroppe, som de handler på, har mærkbare dimensioner. Dette er tilfældet med en bro, hvor køretøjer cirkulerer kontinuerligt, vandet i en swimmingpool på de lodrette vægge af den samme eller et tag, hvor vand eller sne akkumuleres..
Af denne grund fordeles kræfter pr. Længdeenhed, overfladeareal eller volumen afhængigt af det legeme, som de virker på..
I tilfælde af en bjælke kan en kraft fordelt pr. Længdeenhed have forskellige fordelinger, for eksempel den højre trapezoid vist nedenfor:
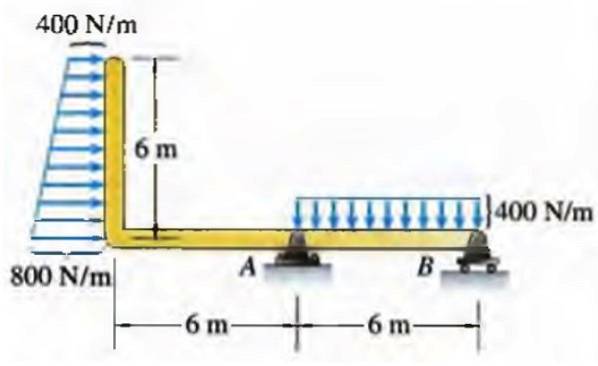
I virkeligheden svarer fordelinger ikke altid til regelmæssige geometriske former som denne, men de kan være en god tilnærmelse i mange tilfælde..
Som et uddannelses- og læringsredskab
Blokke og billeder med geometriske former, herunder trapezoider, er meget nyttige for børn at blive fortrolige med den fascinerende verden af geometri fra en tidlig alder.

Løst øvelser
- Øvelse 1
I højre trapesform i figur 1 er den større base 50 cm og den mindre base lig med 30 cm, det er også kendt, at den skrå side er 35 cm. Finde:
a) Vinkel α
b) Højde
c) Omkreds
d) Gennemsnitlig base
e) Område
f) Diagonaler
Løsning til
Opgørelsesdataene opsummeres som følger:
a = hovedbase = 50 cm
b = mindre bund = 30 cm
d = skrå side = 35 cm
For at finde vinklen α besøger vi formlerne og ligningerne for at se, hvilken der bedst passer til de leverede data. Den søgte vinkel findes i flere af de analyserede trekanter, for eksempel CDP.
Der har vi denne formel, som indeholder det ukendte og også de data, vi kender:
cos α = (a-b) / d
Derfor:
α = buer [(a-b) / d] = buer [(50-30) / 35] = buer 20/35 = 55,15 º
Løsning b
Fra ligningen:
sin α = h / d
Det rydder h:
h = d. sin α = 35 sin 55,15 º cm = 28,72 cm
Løsning c
Omkredsen er summen af siderne, og da højden er lig med siden c, har vi:
c = h = 28,72 cm
Derfor:
P = (50 + 30 + 35 + 28,72) cm = 143,72 cm
Løsning d
Den gennemsnitlige base er semisummen af baserne:
Mellembund = (50 + 30 cm) / 2 = 40 cm
Løsning e
Trapezoidets område er:
A = gennemsnitlig base x højde = 40 cm x 28,72 = 1148,8 cmto.
Løsning f
For den diagonale d1 du kan bruge denne formel:
d1to = bto + bto = 2bto
d1to= 2 x (30 cm)to = 1800 cmto
d1 = √1800 cmto = 42,42 cm
Og for den diagonale dto:
dtoto = dto + bto + 2db cos α = (35 cm)to + (30 cm)to + 2 x 35 x 30 cmto cos 55,15 º = 3325 cmto
dto = √ 3325 cmto = 57,66 cm
Dette er ikke den eneste måde at finde dto, da der også er DAB-trekanten.
- Øvelse 2
Den følgende graf over hastighed som funktion af tiden hører til en mobil, der har ensartet accelereret retlinet bevægelse. Beregn mobiltelefonens afstand i tidsintervallet mellem 0,5 og 1,2 sekunder.
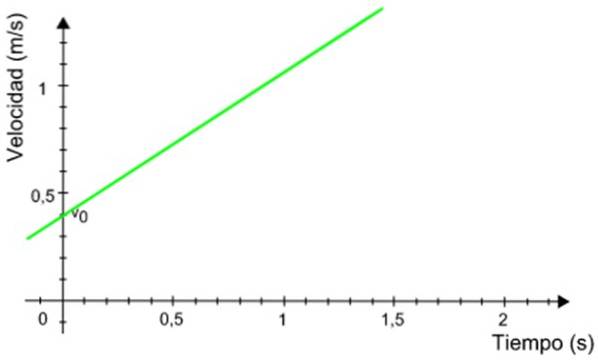
Opløsning
Den tilbagelagte afstand med mobiltelefonen svarer numerisk til området under grafen, afgrænset af det angivne tidsinterval.
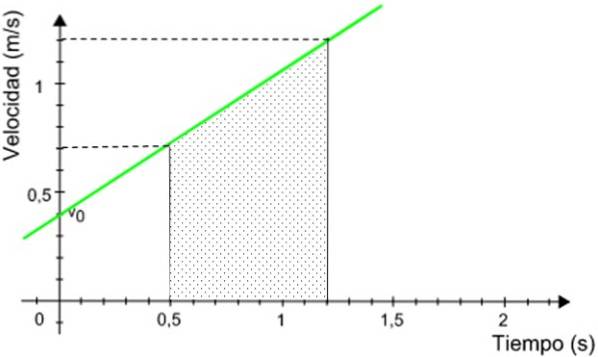
Det skraverede område er området for en højre trapezformet, givet af:
A = (Major base + mindre base) x højde / 2
A = (1,2 + 0,7) m / s x (1,2 - 0,5) s / 2 = 0,665 m
Referencer
- Baldor, A. 2004. Plane- og rumgeometri med trigonometri. Kulturelle publikationer.
- Bedford, A. 1996. Statik. Addison Wesley Interamericana.
- Jr. geometri. 2014. Polygoner. Lulu Press, Inc..
- OnlineMSchool. Rektangulær trapez. Gendannet fra: es.onlinemschool.com.
- Automatisk geometri problemløsning. Trapesen. Gendannet fra: scuolaelettrica.it
- Wikipedia. Trapez (geometri). Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer