Det normal vektor er den, der definerer retningen vinkelret på en eller anden geometrisk enhed under overvejelse, som f.eks. kan være en kurve, et plan eller en overflade.
Det er et meget nyttigt koncept i placeringen af en bevægelig partikel eller en eller anden overflade i rummet. I den følgende graf er det muligt at se, hvordan den normale vektor til en vilkårlig kurve er C:
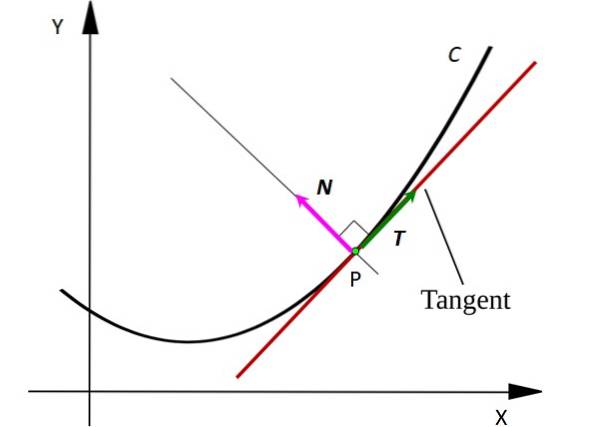
Overvej et punkt P på kurven C. Punktet kan repræsentere en bevægelig partikel, der bevæger sig langs en C-formet sti. Tangentlinien til kurven ved punkt P er tegnet med rødt..
Bemærk, at vektoren T er tangent til C på hvert punkt, mens vektoren N er vinkelret på T y peger på midten af en imaginær cirkel, hvis bue er et segment af C. Vektorer er angivet med fed skrift i trykt tekst for at skelne dem fra andre ikke-vektorstørrelser.
Vektoren T det indikerer altid, hvor partiklen bevæger sig, derfor angiver den dens hastighed. I stedet for vektoren N peger altid i den retning, hvor partiklen roterer, på denne måde angiver den konkaviteten af kurven C.
Artikelindeks
Den normale vektor er ikke nødvendigvis en enhedsvektor, det vil sige en vektor, hvis modul er 1, men i så fald kaldes det normal enhedsvektor.
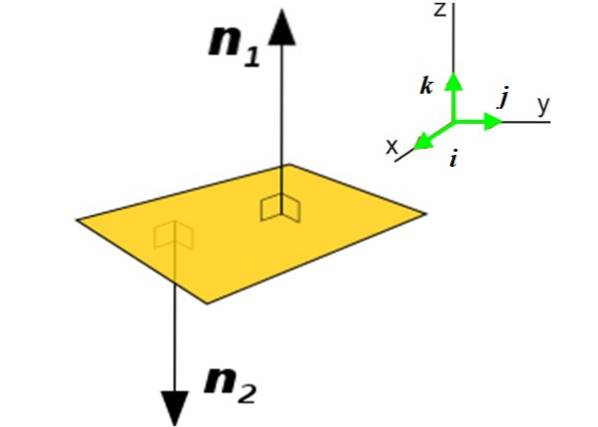
I mange applikationer er det nødvendigt at kende den normale vektor til et plan i stedet for en kurve. Denne vektor afslører orienteringen af planet i rummet. Overvej f.eks. Flyet P (gul) i figuren:
Der er to normale vektorer til dette plan: n1 Y nto. Anvendelsen af det ene eller det andet vil afhænge af den sammenhæng, hvor nævnte plan findes. At få den normale vektor til et plan er meget enkel, hvis du kender dens ligning:
ax + ved + cz + d = 0, med til, b, c Y d reelle tal.
Nå, en normal vektor til nævnte plan er givet af:
N = a jeg + b j + c k
Her vektoren N Det udtrykkes i form af enhedsvektorerne og vinkelret på hinanden jeg, j Y k, rettet langs de tre retninger, der bestemmer rummet X og Z, se figur 2 til højre.
En meget enkel procedure til at finde den normale vektor bruger egenskaberne af vektorproduktet mellem to vektorer.
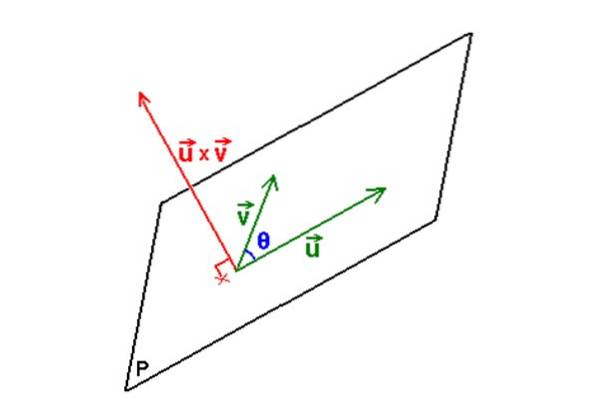
Som det er kendt, bestemmer tre forskellige punkter og ikke kollinære med hinanden et plan P. Nu er det muligt at opnå to vektorer eller Y v der hører til nævnte fly med disse tre punkter.
Når du har vektorerne, er vektor produkt eller x v er en operation, hvis resultat igen er en vektor, som har den egenskab, at den er vinkelret på det plan, der er bestemt af eller Y v.
Kendt denne vektor er den betegnet som N, og ud fra det vil det være muligt at bestemme ligningen af planet takket være ligningen angivet i det foregående afsnit:
N = eller x v
Følgende figur illustrerer den beskrevne procedure:
Find ligningen af planet bestemt af punkterne A (2,1,3); B (0,1,1); C (4,2,1).
Denne øvelse illustrerer proceduren beskrevet ovenfor. Ved at have 3 point vælges en af dem som den fælles oprindelse for to vektorer, der hører til det plan, der er defineret af disse punkter. For eksempel er punkt A indstillet som oprindelsen, og vektorerne er konstrueret AB Y AC.
Vektoren AB er vektoren, hvis oprindelse er punkt A, og hvis slutpunkt er punkt B. Vektorens koordinater AB bestemmes ved henholdsvis at trække koordinaterne for B fra koordinaterne for A:
AB = (0-2) jeg + (1-1) j + (1-3) k = -2jeg + 0j -to k
Vi fortsætter på samme måde for at finde vektoren AC:
AC = (4-2) jeg + (2-1) j + (1-3) k = 2jeg + j -to k
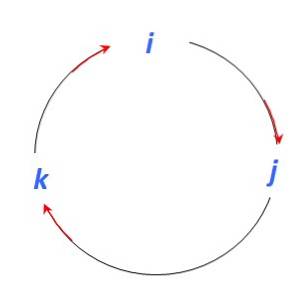
Der er flere procedurer til at finde vektorproduktet mellem to vektorer. Dette eksempel bruger en mnemonisk procedure, der gør brug af følgende figur til at finde vektorprodukterne mellem enhedsvektorerne jeg, j Y k:
Til at begynde med er det godt at huske, at vektorprodukterne mellem parallelle vektorer er nul, derfor:
jeg x jeg = 0; j x j = 0; k x k = 0
Og da vektorproduktet er en anden vektor vinkelret på de deltagende vektorer, når vi bevæger os i retning af den røde pil, har vi:
jeg x j = k ; j x k = jeg; k x jeg = j
Hvis du skal bevæge dig i modsat retning af pilen, skal du tilføje et tegn (-):
j x jeg = - k; k x j = -jeg; jeg x k = -j
I alt er det muligt at fremstille 9 vektorprodukter med enhedsvektorerne jeg, j Y k, hvoraf 3 vil være nul.
AB x AC = (-2jeg + 0j -to k) x (2jeg + j -to k) = -4 (jeg x jeg) to (jeg x j) +4 (jeg x k) +0 (j x jeg) + 0 (j x j) - 0 (j x k) - 4 (k x jeg) - to (k x j) + 4 (k x k) = -2k-4j-4j+tojeg = 2jeg -8j-tok
Vektoren N er bestemt af det tidligere beregnede vektorprodukt:
N = tojeg -8j-tok
Derfor er a = 2, b = -8, c = -2, det søgte plan er:
ax + ved + cz + d = 0 → 2x-8y-2z + d = 0
Værdien af d. Dette er let, hvis værdierne for et af punkterne A, B eller C, der er tilgængelige, er substitueret i ligningen af planet. At vælge C for eksempel:
x = 4; y = 2; z = 1
Rester:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
Kort sagt er det søgte kort:
2x-8y-2z +10 = 0
Den nysgerrige læser spekulerer måske på, om det samme resultat ville være opnået hvis i stedet for at gøre AB x AC de ville have valgt at gennemføre AC x AB. Svaret er ja, planet bestemt af disse tre punkter er unikt og har to normale vektorer, som vist i figur 2.
Hvad angår det punkt, der er valgt som vektorernes oprindelse, er der ikke noget problem at vælge nogen af de to andre.
Endnu ingen kommentarer