
Collinear Vectors System og eksempler
Det kollinære vektorer De er en af de tre typer af eksisterende vektorer. Dette er de vektorer, der er i samme retning eller handlingslinje. Dette betyder følgende: to eller flere vektorer vil være kollinære, hvis de er arrangeret i linjer, der er parallelle med hinanden.
En vektor defineres som en mængde, der påføres et legeme og er kendetegnet ved at have en retning, en sans og en skala. Vektorer kan findes i planet eller i rummet og kan være af forskellige typer: kollinære vektorer, samtidige vektorer og parallelle vektorer.

Artikelindeks
- 1 kollinære vektorer
- 2 funktioner
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 1
- 3 Kollinært vektorsystem
- 3.1 Kollinære vektorer med modsatte retninger
- 3.2 Kollinære vektorer med samme retning
- 3.3 Kollinære vektorer med lige store størrelser og modsatte retninger
- 4 Forskel mellem kollinære og samtidige vektorer
- 5 Referencer
Kollineære vektorer
Vektorer er kollinære, hvis handlingslinjen for en er nøjagtig den samme handlingslinje for alle de andre vektorer, uanset størrelsen og retningen af hver af vektorerne.
Vektorer bruges som repræsentationer i forskellige områder såsom matematik, fysik, algebra og også i geometri, hvor vektorer kun er collinære, når deres retning er den samme, uanset om deres sans ikke er..
Egenskaber
- To eller flere vektorer er kollinære, hvis forholdet mellem koordinaterne er ens.
Eksempel 1
Vi har vektorerne m = m_x; m_y og n = n_x; n_y. Disse er collinære, hvis:
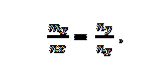
Eksempel 2
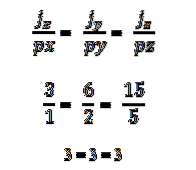
- To eller flere vektorer er kollinære, hvis vektorproduktet eller multiplikationen er lig med nul (0). Dette skyldes, at i koordinatsystemet er hver vektor karakteriseret ved sine respektive koordinater, og hvis disse er proportionale med hinanden, vil vektorerne være kollinære. Dette udtrykkes på følgende måde:
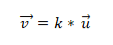
Eksempel 1
Vi har vektorerne a = (10, 5) og b = (6, 3). For at bestemme, om de er kollinære, anvendes determinantteorien, der fastlægger ligeværdigheden af krydsprodukterne. Således skal du:
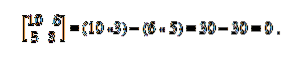
Kollinært vektorsystem
Kollineære vektorer er grafisk repræsenteret ved hjælp af retningen og følelsen af disse - under hensyntagen til at de skal passere gennem applikationsstedet - og modulet, som er en bestemt skala eller længde..
Systemet med kollinære vektorer dannes, når to eller flere vektorer virker på et objekt eller legeme, der repræsenterer en kraft og virker i samme retning..
For eksempel, hvis der påføres to kollinære kræfter på et legeme, vil resultatet af disse kun afhænge af den retning, de virker i. Der er tre tilfælde, som er:
Kollinære vektorer med modsatte retninger
Den resulterende af to kollinære vektorer er lig med summen af disse:
R = ∑ F = F1 + Fto.
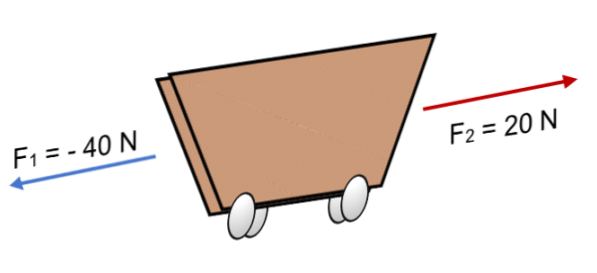
Eksempel
Hvis to kræfter F virker på en vogn1 = 40 N og F.to = 20 N i modsat retning (som vist på billedet), resultatet er:
R = ∑ F = (- 40 N) + 20N.
R = - 20 N.
Kollinære vektorer med samme sans
Størrelsen af den resulterende kraft vil være lig med summen af de kollinære vektorer:
R = ∑ F = F1 + Fto.
Eksempel
Hvis to kræfter F virker på en vogn1 = 35 N og F.to = 55 N i samme retning (som vist på billedet), resultatet er:
R = ∑ F = 35 N + 55N.
R = 90 N.
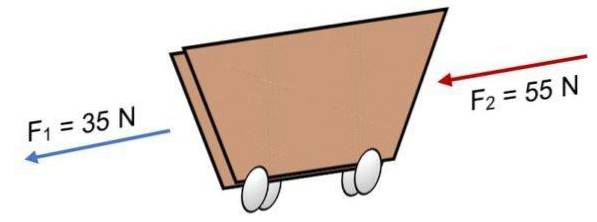
Det positive resultat indikerer, at de kollinære vektorer virker til venstre.
Kollinære vektorer med lige store størrelser og modsatte retninger
Den resulterende af de to kollinære vektorer vil være lig med summen af de kollinære vektorer:
R = ∑ F = F1 + Fto.
Da kræfterne har samme størrelse, men i den modsatte retning - det vil sige, at den ene vil være positiv og den anden negativ-, når de to kræfter tilføjes, vil den resulterende være lig med nul..
Eksempel
Hvis to kræfter F virker på en vogn1 = -7 N og F.to = 7 N, som har samme størrelse, men i modsat retning (som vist på billedet), er resultatet:
R = ∑ F = (-7 N) + 7N.
R = 0.
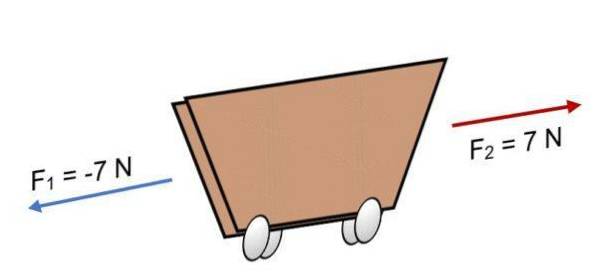
Da den resulterende er lig med 0, betyder det, at vektorerne balancerer hinanden, og derfor er kroppen i ligevægt eller i ro (den bevæger sig ikke).
Forskel mellem kollinære og samtidige vektorer
Kollineære vektorer er kendetegnet ved at have samme retning i samme linje, eller fordi de er parallelle med en linje; de er direktørvektorer med parallelle linjer.
Samtidige vektorer defineres, fordi de er i forskellige handlingslinjer, der krydser hinanden på et enkelt punkt..
Med andre ord har de samme udgangspunkt eller ankomst - uanset modul, retning eller retning - danner en vinkel imellem dem..
Samtidige vektorsystemer løses ved matematiske eller grafiske metoder, som er parallelogram af kræfter og polygon af kræfter. Gennem disse bestemmes værdien af en resulterende vektor, som angiver retningen, i hvilken en krop bevæger sig.
Grundlæggende er den største forskel mellem kollinære og samtidige vektorer den handlingslinie, hvori de virker: De kollinære fungerer i den samme linje, mens de samtidige i forskellige.
Det vil sige, at de kollinære vektorer virker i et enkelt plan, "X" eller "Y"; og de sideløbende handler i begge plan startende fra det samme punkt.
Kollineære vektorer mødes ikke på et tidspunkt, som samtidige vektorer gør, fordi de er parallelle med hinanden.
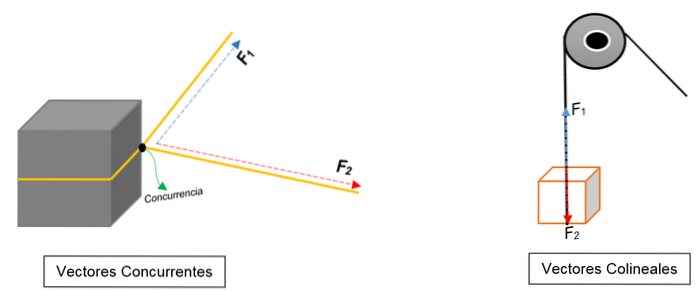
I det venstre billede kan du se en blok. Det er bundet med et reb, og knuden deler det i to; når trækkes mod forskellige retninger og med forskellige kræfter, vil blokken bevæge sig i samme retning.
To vektorer, der stemmer overens på et punkt (blokken), bliver repræsenteret, uanset deres modul, retning eller retning.
På den anden side er der i det rigtige billede en remskive, der løfter en kasse. Rebet repræsenterer handlingslinjen; når den trækkes, virker to kræfter (vektorer) på den: en spændingskraft (når blokken hæves) og en anden kraft, som udøver vægten af blokken. Begge har samme retning, men i modsatte retninger; de er ikke enige på et tidspunkt.
Referencer
- Estalella, J. J. (1988). Vector analyse. Bind 1.
- Gupta, A. (s.f.). Tata McGraw-Hill Uddannelse.
- Jin Ho Kwak, S. H. (2015). Lineær algebra. Springer Science & Business Media.
- Montiel, H. P. (2000). Fysik 1 til teknologisk studentereksamen. Grupo Redaktionel Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Generel fysik. Redaktionel Tebar.
- Sinha, K. (s.f.). A Text Book of Mathematics XII Vol. 2. Rastogi Publications.



Endnu ingen kommentarer