
Øjeblikkelig hastighedsdefinition, formel, beregning og øvelser
Det øjeblikkelig hastighed det er defineret som den øjeblikkelige ændring af forskydningen i tid. Det er et koncept, der tilføjer stor præcision til studiet af bevægelse. Og det er et fremskridt med hensyn til gennemsnitshastigheden, hvis oplysninger er meget generelle.
For at få den øjeblikkelige hastighed, lad os se på et så lille tidsinterval som muligt. Differentialregning er det perfekte værktøj til at udtrykke denne idé matematisk.

Udgangspunktet er den gennemsnitlige hastighed:

Denne grænse er kendt som et derivat. I den differentielle beregningsnotation har vi:
))
Hver gang bevægelsen er begrænset til en lige linje, kan vektornotationen udelades.
Artikelindeks
- 1 Beregning af øjeblikkelig hastighed: geometrisk fortolkning
- 2 Nogle specielle tilfælde til beregning af øjeblikkelig hastighed
- 3 Løst øvelser med øjeblikkelig hastighed
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referencer
Beregning af øjeblikkelig hastighed: geometrisk fortolkning
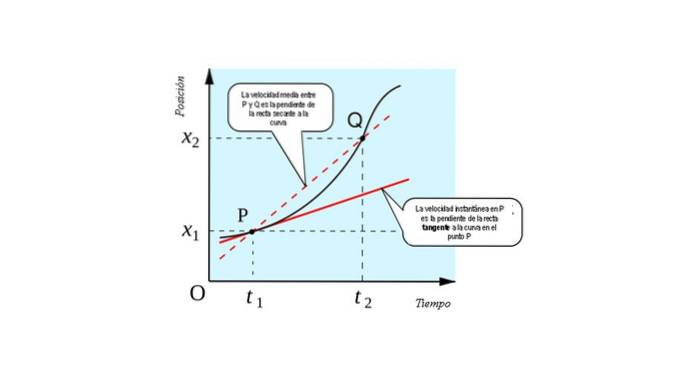
Følgende figur viser den geometriske fortolkning af det afledte koncept: det er linjens hældning tangent til kurven x (t) vs. t på hvert punkt.

Du kan forestille dig, hvordan du opnår grænsen, hvis punkt Q nærmer sig lidt efter lidt til punkt P. Der vil komme et tidspunkt, hvor begge punkter er så tætte, at du ikke kan skelne hinanden fra hinanden..
Linjen, der slutter sig til dem, går derefter fra at være sekant (linje, der krydser ved to punkter) til at være tangent (linje, der kun berører kurven ved et punkt). Derfor skal vi have den øjeblikkelige hastighed af en bevægelig partikel:
- Grafen over positionen af partiklen som en funktion af tiden. At finde hældningen af tangentlinjen til kurven på hvert tidspunkt, vi har den øjeblikkelige hastighed på hvert punkt, som partiklen optager.
O brønd:
- Partikelpositionsfunktionen x (t), som er afledt for at opnå hastighedsfunktionen v (t), derefter evalueres denne funktion i hvert slag t, ved bekvemmelighed. Positionsfunktionen antages at være differentierbar.
Nogle specielle tilfælde ved beregning af øjeblikkelig hastighed
-Tangentlinjens hældning til kurven ved P er 0. En hældning på nul betyder, at mobilen er stationær, og at dens hastighed naturligvis er 0.
-Hældningen på linjen, der tangerer til kurven ved P, er større end 0. Hastigheden er positiv. I grafen ovenfor betyder det, at mobilen bevæger sig væk fra O.
-Tangentlinjens hældning til kurven ved P er mindre end 0. Hastigheden ville være negativ. I grafen ovenfor er der ingen sådanne punkter, men i dette tilfælde vil partiklen nærme sig O.
-Hældningen på linjen, der tangerer til kurven, er konstant ved P og alle andre punkter. I dette tilfælde er grafen en lige linje, og mobilen har ensartet linjebevægelse MRU (dens hastighed er konstant).
Generelt er funktionen v (t) det er også en funktion af tiden, som igen kan have et derivat. Hvad hvis det ikke var muligt at finde derivaterne af funktionerne x (t) Y v (t)?
I tilfælde af x (t) det kan være, at skråningen - den øjeblikkelige hastighed - skifter pludselig. Eller at det straks går fra nul til en anden værdi.
I så fald grafen x (t) det ville præsentere punkter eller hjørner på steder med pludselige ændringer. Meget forskellig fra tilfældet repræsenteret i det forrige billede, hvor kurven x (t) er en glat kurve uden punkter, hjørner, diskontinuiteter eller pludselige ændringer.
Sandheden er, at for ægte mobiltelefoner er de glatte kurver dem, der bedst repræsenterer objektets opførsel.
Bevægelsen generelt er ret kompleks. Mobilerne kan stoppes et stykke tid, accelerere for at gå fra hvile for at få en hastighed og bevæge sig væk fra startpunktet, opretholde hastigheden et stykke tid, derefter bremse for at stoppe igen og så videre..
Igen kan de starte igen og fortsætte i samme retning. Eller aktiver omvendt og vend tilbage. Dette kaldes varieret bevægelse i en dimension..
Her er nogle eksempler på beregning af den øjeblikkelige hastighed, der tydeliggør brugen af de givne definitioner:
Løst øvelser med øjeblikkelig hastighed
Øvelse 1
En partikel bevæger sig langs en lige linje med følgende bevægelseslov:
x (t) = -t3 + 2 tto + 6 t - 10
Alle enheder er i det internationale system. Finde:
a) Partiklens position ved t = 3 sekunder.
b) Den gennemsnitlige hastighed i intervallet mellem t = 0 s og t = 3 s.
c) Den gennemsnitlige hastighed i intervallet mellem t = 0 s og t = 3 s.
d) Partikelens øjeblikkelige hastighed fra det foregående spørgsmål ved t = 1 s.
Svar
a) For at finde partiklens position evalueres bevægelsesloven (positionsfunktion) ved t = 3:
x (3) = (-4/3) .33 + 2. 3to + 6,3 - 10 m = -10 m
Der er ikke noget problem med, at positionen er negativ. Tegnet (-) angiver, at partiklen er til venstre for oprindelsen O.
b) Ved beregningen af gennemsnitshastigheden kræves partikelens endelige og indledende position på de angivne tidspunkter: x (3) og x (0). Positionen ved t = 3 er x (3) og er kendt fra det foregående resultat. Positionen ved t = 0 sekunder er x (0) = -10 m.
Da den endelige position er den samme som den oprindelige position, konkluderes det straks, at gennemsnitshastigheden er 0.
c) Den gennemsnitlige hastighed er forholdet mellem den tilbagelagte afstand og den tid, det tager. Afstanden er nu modulet eller størrelsen på forskydningen, derfor:
afstand = | x2 - x1 | = | -10 - (-10) | m = 20 m
Bemærk, at den tilbagelagte afstand altid er positiv.
vm = 20 m / 3 s = 6,7 m / s
d) Her er det nødvendigt at finde det første afledte af positionen med hensyn til tid. Derefter vurderes det i t = 1 sekund.
x '(t) = -4 tto + 4 t + 6
x '(1) = -4,1to + 4,1 + 6 m / s = 6 m / s
Øvelse 2
Nedenfor er grafen over en mobils position som en funktion af tiden. Find den øjeblikkelige hastighed ved t = 2 sekunder.
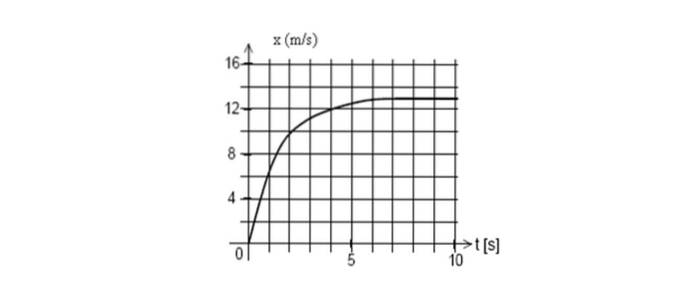
Svar
Tegn tangentlinien til kurven ved t = 2 sekunder, og beregn derefter hældningen, idet du tager to punkter på linjen.
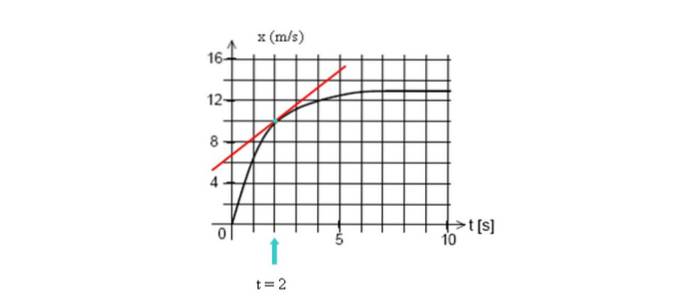
I dette eksempel tager vi to punkter, der let kan visualiseres, hvis koordinater er (2 s, 10 m) og snittet med den lodrette akse (0 s, 7 m):

Referencer
- Giancoli, D. Fysik. Principper med applikationer. 6th Udgave. Prentice Hall. 22-25.
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 21-22.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Udgave. Mexico. Cengage Learning Editors. 23-25.



Endnu ingen kommentarer