
Relativt hastighedskoncept, eksempler, øvelser
Det relativ hastighed af et objekt er et, der måles i forhold til en given observatør, da en anden observatør kan opnå en anden måling. Hastighed afhænger altid af observatøren, der måler den.
Derfor vil en genstands hastighed målt af en bestemt person være den relative hastighed i forhold til den. En anden observatør kan opnå en anden værdi for hastigheden, selvom det er det samme objekt.
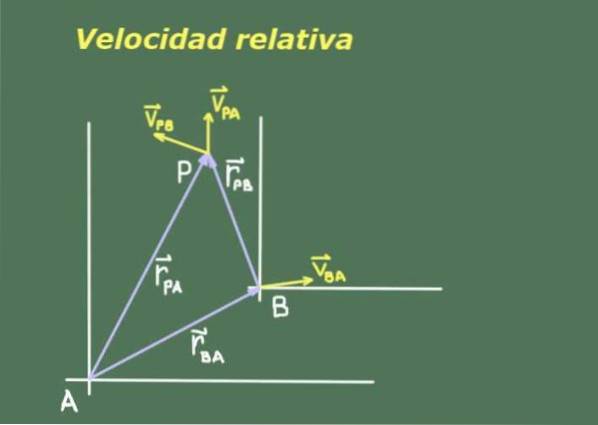
Da to observatører A og B, der bevæger sig i forhold til hinanden, kan have forskellige målinger af en tredje bevægende genstand P, er det nødvendigt at kigge efter et forhold mellem positionerne og hastighederne for P set af A og B.
Figur 1 viser to observatører A og B med deres respektive referencesystemer, hvorfra de måler positionen og hastigheden af objektet P.
Hver observatør A og B måler positionen og hastigheden af objektet P på et givet tidspunkt t. I klassisk (eller galilensk) relativitetstid er tiden for observatør A den samme som for observatør B uanset deres relative hastighed.
Denne artikel handler om klassisk relativitet, der er gyldig og anvendelig i de fleste hverdagssituationer, hvor objekter har hastigheder, der er meget langsommere end lysets..
Vi betegner placeringen af observatør B med hensyn til A som rBA. Da position er en vektormængde, bruger vi fed for at indikere det. Objektets P position i forhold til A betegnes som rPA og det samme objekt P med hensyn til B rPB.
Artikelindeks
- 1 Forholdet mellem relative positioner og hastigheder
- 1.1 Sådan ser et barn det fra en bevægelig bil
- 2 Relativ hastighed mellem motorcyklen og bilen
- 2.1-Øvelse løst
- 3 Referencer
Forholdet mellem relative positioner og hastigheder
Der er et vektorforhold mellem disse tre positioner, der kan udledes af repræsentationen i figur 1:
rPA= rPB + rBA
Hvis afledningen af det foregående udtryk tages med hensyn til tid t vi opnår forholdet mellem den relative hastighed for hver observatør:
VPA= VPB + VBA
I det foregående udtryk har vi den relative hastighed af P med hensyn til A som en funktion af den relative hastighed af P med hensyn til B og den relative hastighed af B med hensyn til A.
Tilsvarende kan den relative hastighed af P i forhold til B skrives som en funktion af den relative hastighed af P i forhold til A og den relative hastighed af A i forhold til B.
VPB= VPA + VAB
Det skal bemærkes, at den relative hastighed af A i forhold til B er lig med og i modsætning til den for B med hensyn til A:
VAB = -VBA
Sådan ser et barn det fra en bevægelig bil
En bil kører på en lige vej, der går fra vest til øst, med en hastighed på 80 km / t, mens en motorcykel i modsat retning (og fra den anden bane) kommer med en hastighed på 100 km / t.
En dreng rejser på bagsædet i bilen, der ønsker at kende den relative hastighed på en motorcykel, der nærmer sig ham. For at finde ud af svaret anvender barnet de forhold, som han netop har læst i det foregående afsnit, idet hvert koordinatsystem identificeres som følger:
-A er koordinatsystemet for en observatør på vejen, og i forhold til det er hvert køretøjs hastighed blevet målt.
-B er bilen og P er motorcyklen.
Hvis du vil beregne motorcykel P's hastighed i forhold til bil B, anvendes følgende forhold:
VPB= VPA + VAB=VPA - VBA
Idet vi tager den vest-østlige retning som positiv, har vi:
VPB= (-100 km / t - 80 km / t) jeg = -180 km / t jeg
Dette resultat fortolkes som følger: motorcyklen bevæger sig i forhold til bilen med en hastighed på 180 km / t og retning -jeg, det vil sige fra øst til vest.
Relativ hastighed mellem motorcyklen og bilen
Motorcyklen og bilen har krydset hinanden efter deres bane. Barnet på bagsædet i bilen ser motorcyklen bevæge sig væk og vil nu vide, hvor hurtigt den bevæger sig væk fra ham, forudsat at både motorcyklen og bilen holder de samme hastigheder som før krydsning..
For at kende svaret anvender barnet det samme forhold som tidligere anvendt:
VPB= VPA + VAB=V PA - VBA
VPB= -100 km / t jeg - 80 km / t jeg = -180 km / t jeg
Og nu bevæger motorcyklen sig væk fra bilen med den samme relative hastighed, som den nærmede sig, før de krydsede..
Den samme motorcykel fra del 2 returneres med den samme hastighed på 100 km / t, men ændrer retning. Det vil sige, at bilen (som fortsætter med en hastighed på 80 km / t) og motorcyklen bevæger sig begge i positiv øst-vest retning..
På et bestemt tidspunkt passerer motorcyklen bilen, og barnet i bilens bagsæde vil vide motorcykelens relative hastighed i forhold til ham, når han ser det passere forbi..
For at få svaret anvender barnet forholdet mellem relativ bevægelse igen:
VPB= VPA + VAB=VPA - VBA
VPB= +100 km / t jeg - 80 km / t jeg = 20 km / t jeg
Barnet fra bagsædet ser motorcyklen forbi bilen med en hastighed på 20 km / t.
-Træning løst
Øvelse 1
En motorbåd krydser en flod, der er 600 m bred og flyder fra nord til syd. Flodens hastighed er 3 m / s. Bådens hastighed i forhold til vandet i floden er 4 m / s mod øst.
(i) Find bådens hastighed i forhold til flodbredden.
(ii) Angiv fartens hastighed og retning i forhold til land.
(iii) Beregn crossover-tiden.
(iv) Hvor langt syd det vil være flyttet fra startpunktet.
Opløsning
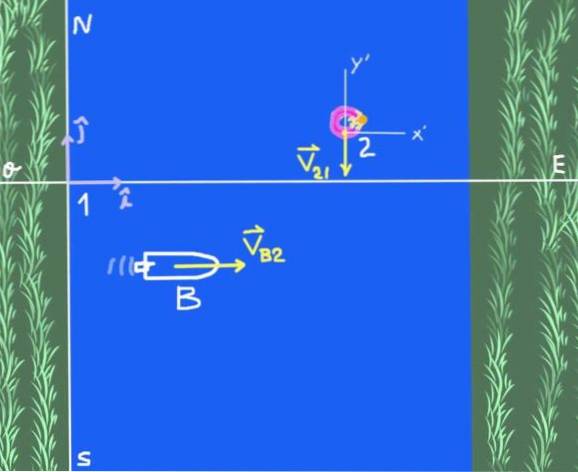
Der er to referencesystemer: det solidære referencesystem på flodbredden, som vi kalder 1, og referencesystemet 2, som er en observatør, der flyder på flodvandet. Formålet med undersøgelsen er båd B.
Bådens hastighed i forhold til floden skrives i vektorform som følger:
VB2 = 4 jeg Frk
Observatørens 2 hastighed (flåde ved floden) i forhold til observatør 1 (på land):
Venogtyve = -3 j Frk
Du vil finde hastigheden på båden i forhold til land VB1.
VB1 = VB2 + Venogtyve
Svar i
VB1 = (4 jeg - 3 j) Frk
Bådens hastighed er modulet for den tidligere hastighed:
|VB1| = (42 + (-3) 2) ½ = 5 m / s
Svar ii
Og adressen vil være:
θ = arctan (-¾) = -36,87º
Svar iii
Bådens krydsetid er kvotienten mellem bredden af floden og x-komponenten af bådens hastighed i forhold til land.
t = (600m) / (4 m / s) = 150 s
Svar iv
For at beregne den drift, som båden havde mod syd, multipliceres y-komponenten af bådens hastighed i forhold til land med krydsetiden:
d = -3 j m / s * 150 s = -450 j m
Forskydningen mod syd i forhold til startpunktet er 450m.
Referencer
- Giancoli, D. Fysik. Principper med applikationer. 6. udgave. Prentice Hall. 80-90
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 100-120.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Udgave. Mexico. Cengage Learning Editors. 95-100.
- Wikipedia. Relativ hastighed. Gendannet fra: wikipedia.com
- Wikipedia. Relativ hastighedsmetode. Gendannet fra: wikipedia.com


Endnu ingen kommentarer