
Bue (geometri) mål, buetyper, eksempler
Det sløjfe, i geometri er det enhver buet linje, der forbinder to punkter. En buet linje er, i modsætning til en lige linje, en hvis retning er forskellig på hvert punkt på den. Det modsatte af en bue er et segment, da dette er et lige afsnit, der forbinder to punkter.
Den lysbue, der oftest anvendes i geometri, er omkredsen. Andre buer til almindelig brug er den parabolske bue, elliptiske bue og kædeledningsbuen. Bueformen bruges også ofte i arkitektur som et dekorativt element og et strukturelt element. Dette er tilfældet med overliggerne på døre og vinduer såvel som broer og akvædukter.

Artikelindeks
- 1 Buen og dens mål
- 2 typer buer
- 2.1 Rundbue
- 2.2 Parabolsk bue
- 2.3 Ledningsbue
- 2.4 Elliptisk bue
- 3 Eksempler på buer
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referencer
Buen og dens mål
Måling af en bue er dens længde, hvilket afhænger af typen af kurve, der forbinder de to punkter og deres placering..
Længden af en cirkelbue er en af de enkleste at beregne, fordi længden af den komplette bue eller omkreds af en omkreds er kendt.
Omkredsen af en cirkel er to pi gange din radio: p = 2 π R. At vide dette, hvis du vil beregne længden s af en cirkulær vinkelbue a (målt i radianer) og radius R, der anvendes et forhold:
(s / p) = (α / 2 π)
Derefter clearing s fra det forrige udtryk og erstatte omkredsen s ved dets udtryk som en funktion af radius R, du har:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R.
Det vil sige, at målingen af en cirkelbue er produktet af dens vinkelåbningstider radius af den cirkelbue.
For en bue generelt er problemet mere kompliceret til det punkt, at antikens store tænkere bekræftede, at det var en umulig opgave..
Det var først med fremkomsten af differential- og integralberegningen i 1665, at problemet med måling af en hvilken som helst lysbue blev løst tilfredsstillende.
Før opfindelsen af differentieret beregning kunne der kun findes løsninger ved hjælp af polygonale linjer eller buer med omkreds, der tilnærmede den sande bue, men disse løsninger var ikke nøjagtige.
Typer af buer
Fra et geometrisk synspunkt klassificeres buer efter den buede linje, der forbinder to punkter på planet. Der er andre klassifikationer efter deres brug og arkitektoniske form.
Rundbue
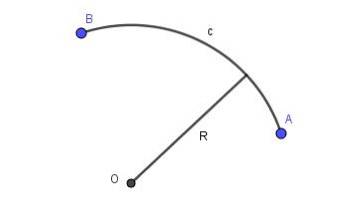
Når linjen, der forbinder to punkter i planet, er et stykke omkreds med en bestemt radius, har vi en cirkelbue. Figur 2 viser en cirkelbue c med radius R-forbindelsespunkterne A og B.
Parabolisk bue
Parabolen er stien fulgt af et objekt, der er smidt skråt i luften. Når kurven, der forbinder to punkter, er en parabel, har vi en parabolbue som den vist i figur 3.
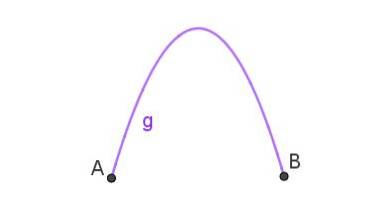
Dette er formen på vandstrålen, der kommer ud af en slange, der peger opad. Den parabolske bue kan observeres i vandkilderne.

Køreledningsbue
Ledningsbuen er en anden naturlig bue. Køreledningen er den kurve, der dannes naturligt, når en kæde eller et reb hænger løst fra to separate punkter.
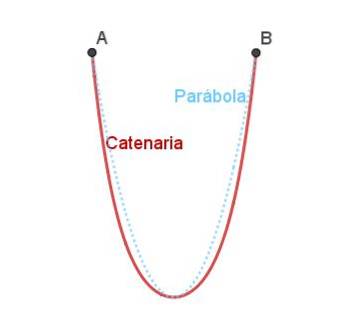
Køreledningen ligner parabolen, men den er ikke nøjagtig den samme som det kan ses i figur 4.
Den omvendte ledningsbue bruges i arkitekturen som et strukturelt element med høj trykstyrke. Faktisk kan det vises at være den stærkeste type bue af alle mulige former..
For at opbygge en solid ledningsbue skal du bare kopiere formen på et hængende reb eller kæde, så vendes den kopierede form for at reproducere den på døren eller vindueskanten.
Elliptisk bue
En bue er elliptisk, hvis kurven, der forbinder to punkter, er et stykke eller en sektion af en ellipse. Ellipsen er defineret som stedet for de punkter, hvis afstand til to givne punkter altid tilføjer en konstant størrelse.
Ellipsen er en kurve, der vises i naturen: det er kurven for planetenes bane omkring Solen, som Johannes Kepler demonstrerede i år 1609.
I praksis kan en ellipse tegnes ved at fastgøre to stivere til jorden eller to stifter på papir og binde en streng til dem. Rebet spændes derefter med markøren eller blyanten, og kurven spores. Et stykke ellipse er en elliptisk bue. Følgende animation illustrerer, hvordan ellipsen tegnes:
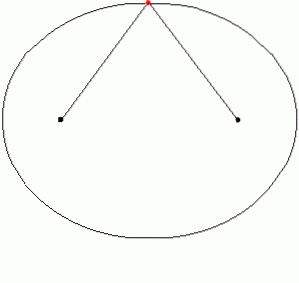
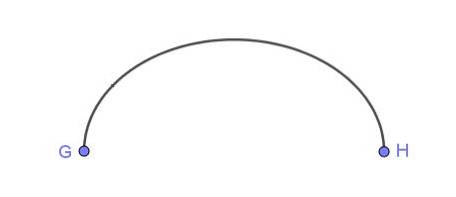
Figur 6 viser en elliptisk lysbue, der forbinder punkterne G og H.
Eksempler på buer
De følgende eksempler henviser til, hvordan man beregner omkredsen af nogle specifikke buer.
Eksempel 1
Figur 7 viser et vindue, der er afsluttet i en skåret cirkelbue. Dimensionerne vist i figur er i fødder. Beregn længden af buen.
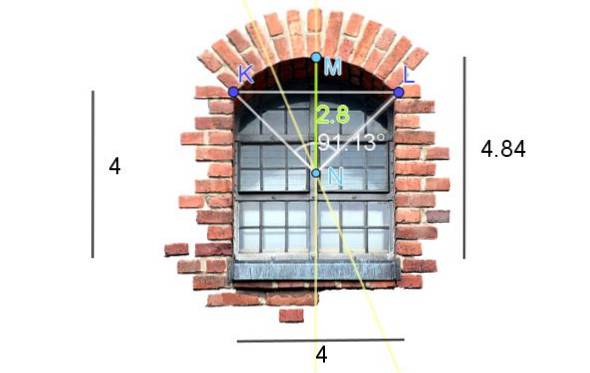
For at få centrum og radius af den runde bue af vinduesoverligningen er der lavet følgende konstruktioner på billedet:
-Segmentet KL er tegnet og dets halveringslinje er tegnet.
-Bagefter er det øverste punkt på overliggeren placeret, som vi kalder M. Dernæst betragtes segmentet KM og dets mediatrix spores..
Skæringspunktet for de to halveringslinjer er punkt N, og det er også centrum for den cirkelbue.
-Nu skal vi måle længden af segmentet NM, der falder sammen med radius R for den cirkelbue: R = 2,8 fod.
-For at kende buens længde ud over radiusen er det nødvendigt at kende den vinkel, som buen danner. Hvilket kan bestemmes ved to metoder, enten måles det med en vinkelmåler, eller alternativt beregnes det ved hjælp af trigonometri.
I det viste tilfælde er vinklen dannet af buen 91,13º, som skal konverteres til radianer:
91,13º = 91,13º * π / 180º = 1,59 radianer
Endelig beregner vi længden s af buen ved hjælp af formlen s = aR.
s = 1,59 * 2,8 fod = 4,45 fod
Eksempel 2
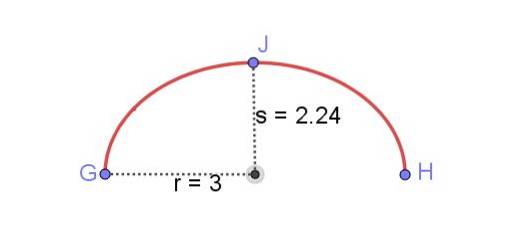
Find længden af den elliptiske bue vist i figur 8, idet du kender den semi-store akse r og den semi-mindre akse s af ellipsen.
At finde længden af en ellips var et af de sværeste problemer i matematik i lang tid. Du kan få løsninger udtrykt ved elliptiske integraler, men for at have en numerisk værdi skal du udvide disse integraler i strømserier. Et nøjagtigt resultat ville kræve uendelige vilkår for disse serier.
Heldigvis fandt det hinduistiske matematiske geni Ramanujan, der boede mellem 1887 og 1920, en formel, der meget nøjagtigt tilnærmer omkredsen af en ellips:
Omkring en ellips = π [3 (r + s) - √ ((3r + s) (r + 3s))]
Omkredsen af en ellipse med r = 3 cm og s = 2,24 cm er 16,55 cm. Den viste elliptiske bue har dog halvdelen af denne værdi:
Længde på elliptisk bue GH = 8,28 cm.
Referencer
- Clemens S. 2008. Geometri og trigonometri. Pearson Uddannelse.
- García F. Numeriske procedurer i Java. Længden af en ellipse. Gendannet fra: sc.ehu.es
- Dynamisk geometri. Buer. Gendannet fra geometriadinamica.es
- Piziadas. Ellipser og paraboler omkring os. Gendannet fra: piziadas.com
- Wikipedia. Bue (geometri). Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer