
Mackinder Box Hvad det er til, hvordan man laver det og bruger
Det Mackinder kasse det er et metodisk element med forskellige anvendelser inden for matematik. Hjælper med at undervise i grundlæggende operationer: addition, subtraktion, multiplikation og division. Det bruges også til at adskille delmængder af sæt og til at trække kardinaler; tjener til at nedbryde og rekomponere additive nummerstrukturer.
Dybest set handler det om at placere en central stor container og 10 mindre containere omkring den. Inden for de mindre beholdere er enhedsmængder repræsenteret, som senere vil blive deponeret i en større beholder, for at repræsentere, at en mængde tilføjes, idet der henvises til den progressive tilføjelse eller multiplikation.
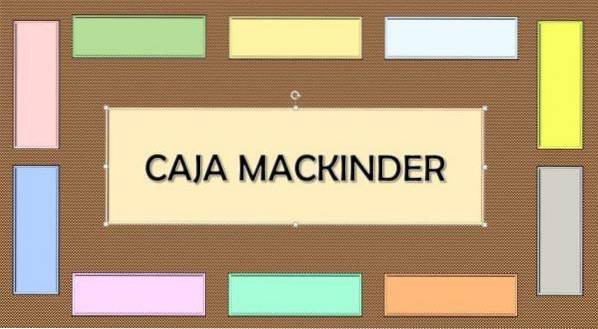
Tværtimod kan det også repræsentere, at der trækkes et beløb fra den større boks med henvisning til divisionen.
Artikelindeks
- 1 Hvad er det til??
- 2 Sådan gør du det?
- 2.1 Med papkasser
- 2.2 Med plastbeholdere
- 2.3 Fremgangsmåde
- 3 Eksempler på anvendelse
- 3.1 Tilføjelse eller tilføjelse
- 3.2 Subtraktion eller subtraktion
- 3.3 Multiplikation
- 3.4 Opdeling
- 4 Referencer
Hvad er det for?
Mackinder-boksen er en metode, der blev udviklet i 1918 i Chelsea, England, af Jessie Mackinder, som var underviser i byen..
Denne metode sigter mod at fremme individualiseringen af uddannelse i emner som matematik, læsning og skrivning ved hjælp af enkle, men interessante materialer som containere, kort og poser, der bruges frit..
Dette instrument består af ti containere, der omgiver en større centralcontainer, alle placeret på en flad bund. Disse elementer bruges til at udføre grundlæggende matematiske operationer, såsom at tilføje, subtrahere, multiplicere og dele. Kan også bruges til at adskille sæt og undersæt.
Mackinder-boksen bruges i de første år af uddannelsen. Det letter forståelsen af matematik, fordi dens metode er baseret på brugen af didaktiske materialer, hvilket giver frihed for hver deltager til at manipulere eller interagere direkte med materialet.
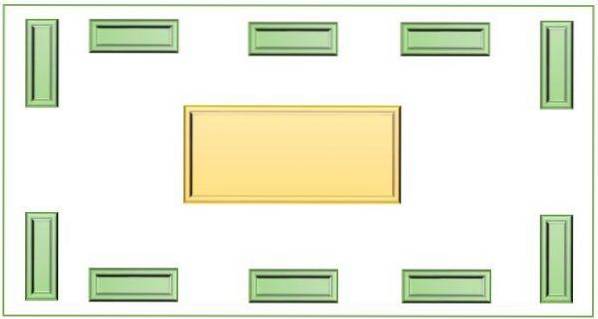
Hvordan gør man det?
Mackinder-kassen består af meget grundlæggende elementer. For at danne det kan du endda bruge genbrugsmateriale eller enhver type container, der tjener til at placere små genstande, der repræsenterer de enheder, der tælles. Blandt de mest almindelige måder at gøre det på er følgende:
Med papkasser
Følgende materialer er nødvendige:
- En rektangulær base, der kan være lavet af pap (skokasse) eller pap.
- 10 små papkasser. De kan være tændstikæsker.
- 1 større æske.
- Lim.
- Tokens, tændstikker, frø eller papirkugler, der kan bruges til optælling.
Med plastbeholdere
De anvendte materialer er følgende:
- En rektangulær base, lavet af pap (skokasse) eller karton.
- 10 plastbeholdere, hold dem små.
- En stor plastbeholder; for eksempel et cd-etui.
- Lim.
- Tokens, tændstikker, frø eller papirkugler, som kan bruges til optælling.

Behandle
- Skær bunden i en rektangulær form.
- Den største beholder (papkassen eller plastbeholderen) er limet i midten.
- Mindre beholdere limes rundt om den store container og får lov til at tørre.
- Beholdere kan males i forskellige farver og få lov til at tørre.
- Chips, tændstikker, frø, papirkugler eller en hvilken som helst genstand, der bruges til at tælle, kan forblive opbevaret i en anden beholder eller inde i den centrale beholder.
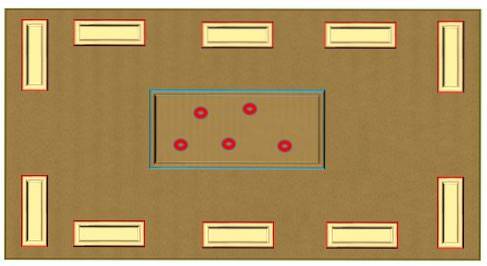
Eksempler på anvendelse
Med boksen Mackinder kan grundlæggende matematiske operationer udføres under hensyntagen til, at beholderne repræsenterer grupper eller sæt, mens elementerne i hver af disse vil være poletter, frø, papirkugler, blandt andre..
Tilføjelse eller tilføjelse
To små kasser bruges til at lave et beløb. I en af disse placeres fliserne, der repræsenterer det første addend, og i den anden boks placeres fliserne for det andet addend..
Du begynder at tælle chipsene i den boks, der har den mindste mængde af disse, og de placeres i den centrale boks; i slutningen af fliserne fra den første boks, fortsæt med den anden.
For eksempel, hvis du i den ene kasse har 5 fliser og i den anden 7, begynder du at tælle fra den ene med 5 fliser, placerer dem i den centrale kasse, indtil du når 5. Derefter fortsætter du med fliserne fra den anden kasse og så indtil. 12.
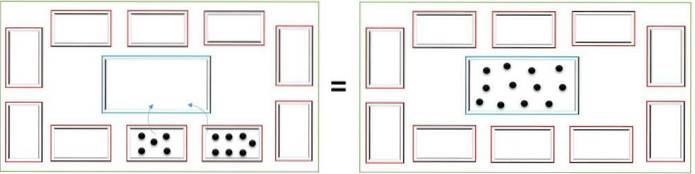
Subtraktion eller subtraktion
For at trække alle fliser, der repræsenterer minuend, placeres i den centrale boks; det vil sige fra det samlede beløb, som et andet beløb trækkes fra (trækker fra).
Fra den store kasse tages mængden af chips, som du vil trække ud, de tælles og placeres i en af de små kasser. For at kende resultatet af subtraktionen tælles antallet af fliser, der var tilbage i den store boks.
For eksempel har du 10 fliser i den centrale boks, og du vil fratrække 6 fliser. Disse fjernes og placeres i en af de små kasser; når der tælles de fliser, der var tilbage i den store kasse, er der i alt 4 fliser, der repræsenterer resultatet af subtraktionen.
Multiplikation
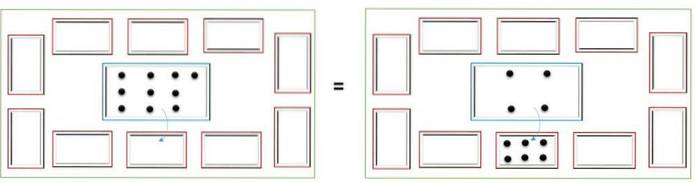
Multiplikation består i at tilføje det samme nummer flere gange. Med boksen Mackinder repræsenterer det første tal i multiplikationen de grupper, der skal dannes; antallet af små kasser, der skal besættes.
I stedet angiver det andet nummer antallet af varer, som hver gruppe vil have, eller fliserne, der skal placeres i hver lille boks. Derefter tælles alle fliserne fra hver lille kasse og placeres i den centrale kasse for at opnå resultatet af multiplikationen.
For eksempel for at multiplicere 4 x 3 skal du placere 3 fliser i 4 små kasser; så begynder de at tælle chipsene i den første kasse og placere dem i den store kasse; dette gentages med de 3 felter. I den centrale boks har du: 3 + 3 + 3 + 3 = 12 chips.
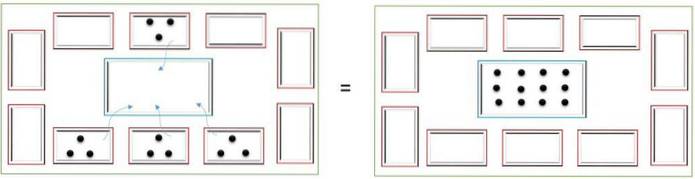
Division
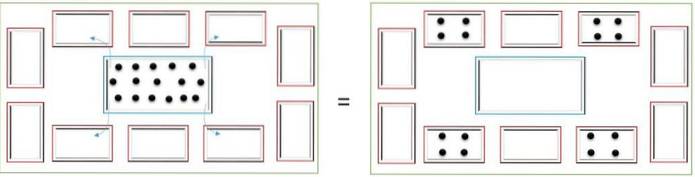
Opdeling handler om at opdele et antal elementer ens. For eksempel for at opdele 16 chips i 4 små kasser placeres disse i den centrale kasse, og de fordeles i små kasser på en sådan måde, at den samme mængde chips forbliver i hver kasse..
I slutningen tælles antallet af chips i hver boks for at bestemme resultatet; i dette tilfælde vil hver have 4 chips.
Referencer
- Alicia Cofré, L. T. (1995). Sådan udvikles matematisk logisk begrundelse.
- Carolina Espinosa, C. C. (2012). Ressourcer i læringsoperationer.
- (1977). Generel didaktik. Tupac.
- Mackinder, J. M. (1922). Individuelt arbejde på spædbørnsskoler.
- María E. Calla, M. C. (2011). Læring af logiske matematiske færdigheder hos piger og drenge. Lima: Educa.



Endnu ingen kommentarer