Det fornuftig varme er den termiske energi, der tilføres et objekt, der får det til at øge temperaturen. Det er det modsatte af latent varme, hvor termisk energi ikke øger temperaturen, men fremmer en faseændring, for eksempel fra fast til væske..
Et eksempel tydeliggør konceptet. Antag, at vi har en gryde med vand ved en stuetemperatur på 20 ° C. Når vi placerer det på komfuret, øger den tilførte varme langsomt temperaturen på vandet, indtil det når 100 ° C (kogetemperatur vand ved havets overflade). Den leverede varme kaldes fornuftig varme.
Når vandet når kogepunktet, hæver ikke varmen fra brænderen vandets temperatur, som forbliver på 100 ° C. I dette tilfælde investeres den leverede termiske energi i at fordampe vandet. Den leverede varme er latent, fordi den ikke hævede temperaturen, men i stedet forårsagede en ændring fra den flydende fase til gasfasen.
Det er en eksperimentel kendsgerning, at den sanselige varme, der er nødvendig for at opnå en bestemt temperaturvariation, er direkte proportional med denne variation og med genstandens masse..
Artikelindeks
Det er blevet observeret, at bortset fra massen og temperaturforskellen afhænger den sanselige varme også af materialet. Af denne grund kaldes proportionalitetskonstanten mellem fornuftig varme og masseproduktet og temperaturforskellen specifik varme.
Mængden af fornuftig tilført varme afhænger også af, hvordan processen udføres. For eksempel er det anderledes, hvis processen udføres ved konstant volumen end ved konstant tryk.
Formlen for fornuftig varme i en proces isobarisk, dvs. ved konstant tryk er det følgende:
Q = cp . m (T.F - Tjeg)
I ovenstående ligning Spørgsmål er den fornuftige varme, der tilføres masseobjektet m, der har hævet sin oprindelige temperatur Tjeg indtil den endelige værdi Tf. I ovenstående ligning vises det også cs, hvilket er materialets specifikke varme ved konstant tryk, fordi processen er udført på denne måde.
Bemærk også, at fornuftig varme er positiv, når den absorberes af objektet og forårsager en stigning i temperaturen..
I tilfælde af at der tilføres varme til en gas, der er lukket i en stiv beholder, vil processen være isokorisk, det vil sige ved konstant volumen; og formlen for fornuftig varme vil blive skrevet sådan:
Q = cv. m. (TF - Tjeg)
Kvotienten mellem den specifikke varme ved konstant tryk og den specifikke varme ved konstant volumen for det samme materiale eller stof kaldes adiabatisk koefficient, som normalt betegnes med det græske bogstav gamma γ.
Det adiabatisk koefficient er større end enhed. Den varme, der kræves for at hæve temperaturen på et legeme med et gram masse med en grad, er større i en isobar proces end i en isokorisk..
Dette skyldes, at i det første tilfælde bruges en del af varmen til at udføre mekanisk arbejde.
Ud over specifik varme defineres også kroppens varmekapacitet ofte. Dette er den mængde varme, der er nødvendig for at hæve kropstemperaturen en grad Celsius.
Varmekapacitet er betegnet med C stort bogstav, mens den specifikke varme med c små bogstaver. Forholdet mellem begge størrelser er:
C = c⋅m
Hvor m er kroppens masse.
Molær specifik varme anvendes også, som defineres som den mængde følsom varme, der er nødvendig for at hæve en temperatur på et mol stof med en grad Celsius eller Kelvin..
Den molære specifikke varme for de fleste faste stoffer har en værdi tæt på 3 gange R, hvor R er den universelle gaskonstant. R = 8,314472 J / (mol ℃).
For eksempel har aluminium molær specifik varme 24,2 J / (mol ℃), Kobber 24,5 J / (mol ℃), guld 25,4 J / (mol ℃), og det søde jern 25,1 J / (mol ℃). Bemærk, at disse værdier er tæt på 3R = 24,9 J / (mol ℃).
I modsætning hertil er den molære specifikke varme for de fleste gasser tæt på n (R / 2), hvor er n et heltal og R er den universelle gaskonstant. Hele tallet n er relateret til antallet af frihedsgrader for det molekyle, der udgør gassen.
For eksempel i en monatomisk ideel gas, hvis molekyle kun har de tre translationelle frihedsgrader, er den molære specifikke varme ved konstant volumen 3 (R / 2). Men hvis det er en diatomisk idealgas, er der desuden to rotationsgrader, så cv = 5 (R / 2).
I ideelle gasser gælder følgende forhold mellem molær specifik varme ved konstant tryk og konstant volumen: cs = cv + R.
Særlig omtale fortjener vandet. I flydende tilstand ved 25 ℃ har vandet cs = 4,1813 J / (g ℃), vanddamp ved 100 grader Celsius har cs = 2.080 J / (g ℃) og isvand ved nul grad celsius har cs = 2.050 J / (g ℃).
Materiale kan være i tre tilstande: fast, flydende og gas. Der kræves energi for at ændre tilstand, men hvert stof reagerer på det på en anden måde i henhold til dets molekylære og atomare egenskaber..
Når et fast stof smelter, eller en væske fordamper, forbliver objektets temperatur konstant, indtil alle partiklerne har ændret deres tilstand..
Af denne grund er det muligt for et stof at være i ligevægt i to faser: fast - flydende eller flydende - damp, for eksempel. En mængde af stoffet kan passere fra en tilstand til en anden ved at tilføje eller fjerne lidt varme, mens temperaturen forbliver fast..
Varmen, der tilføres et materiale, får partiklerne til at vibrere hurtigere og øge deres kinetiske energi. Dette betyder en stigning i temperaturen.
Det er muligt, at den energi, de erhverver, er så stor, at de ikke længere vender tilbage til deres ligevægtsposition, og adskillelsen mellem dem øges. Når dette sker, stiger temperaturen ikke, men stoffet går fra fast til væske eller fra væske til gas.
Den varme, der er nødvendig for at dette kan ske, er kendt som latent varme. Derfor er latent varme den varme, hvormed et stof kan ændre fase.
Her er forskellen med fornuftig varme. Et stof, der absorberer fornuftig varme, øger temperaturen og forbliver i samme tilstand.
Latent varme beregnes ved hjælp af ligningen:
Q = m. L
Hvor L det kan være den specifikke fordampningsvarme eller fusionsvarmen. Enhederne i L er energi / masse.
Forskere har givet varme adskillige navne, afhængigt af hvilken type reaktion den deltager i. For eksempel er der reaktionsvarmen, forbrændingsvarmen, størkningsvarmen, opløsningsvarmen, sublimeringsvarmen og mange andre..
Værdierne for mange af disse varmetyper for forskellige stoffer er opstillet.
Antag, at der er et stykke aluminium med en masse på 3 kg. Oprindeligt er det ved 20 ° C, og du vil hæve temperaturen til 100 ° C. Beregn den nødvendige følsomme varme.
Først skal vi kende aluminiumens specifikke varme
cs = 0,897 J / (g ° C)
Derefter vil den mængde varme, der er nødvendig for at opvarme aluminiumstykket, være
Q = cs m (Tf - Ti) = 0,897 * 3000 * (100 - 20) J
Q = 215 280 J
Beregn den nødvendige mængde varme til opvarmning af 1 liter vand fra 25 ° C til 100 ° C ved havoverfladen. Udtryk resultatet også i kilokalorier.
Den første ting at huske er, at 1 liter vand vejer 1 kg, det vil sige 1000 gram.
Q = cs m (Tf - Ti) = 4,1813 J / (g ℃) * 1000 g * (100 ℃ - 25 ℃) = 313597,5 J
Kalorien er en energienhed, der defineres som den fornuftige varme, der er nødvendig for at hæve et gram vand med en grad Celsius. Derfor er 1 kalorie svarende til 4,1813 Joule.
Q = 313597,5 J * (1 kal / 4,1813 J) = 75000 kal = 75 kcal.
Et stykke materiale på 360,16 gram opvarmes fra 37 ℃ til 140 ℃. Den leverede termiske energi er 1150 kalorier.
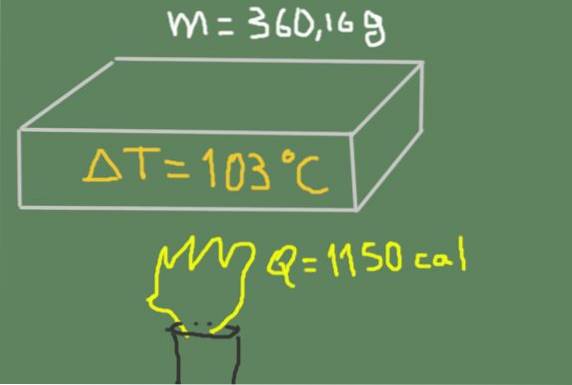
Find materialets specifikke varme.
Vi kan skrive den specifikke varme som en funktion af den sanselige varme, massen og variationen af temperaturen i henhold til formlen:
cs = Q / (m AT)
Udskiftning af data har vi følgende:
cs = 1150 cal / (360,16 g * (140 ℃ - 37 ℃)) = 0,0310 cal / (g ℃)
Men da en kalorie svarer til 4,1813 J, kan resultatet også udtrykkes som
cs = 0,130 J / (g ℃)
Endnu ingen kommentarer