Det enhed celle Det er et imaginært rum eller en region, der repræsenterer minimumsudtrykket af en helhed; at i tilfælde af kemi ville det hele være en krystal sammensat af atomer, ioner eller molekyler, der er arrangeret efter et strukturelt mønster.
Eksempler kan findes i hverdagen, der inkorporerer dette koncept. Til dette er det nødvendigt at være opmærksom på objekter eller overflader, der udviser en bestemt gentagen rækkefølge af deres elementer. Nogle mosaikker, basrelieffer, lofter, ark og tapeter kan generelt omfatte, hvad der forstås ved enhedscelle.
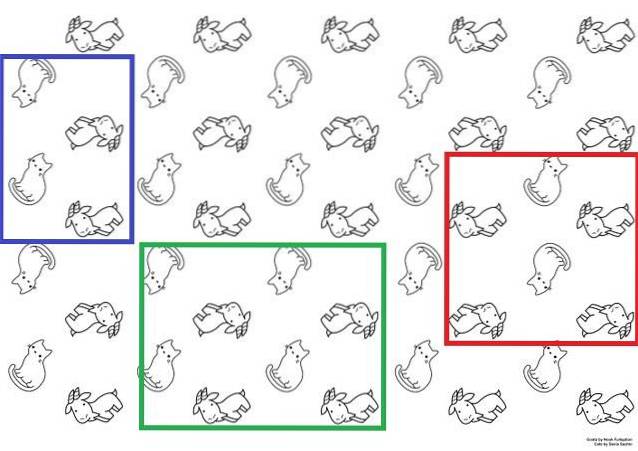
For at illustrere det mere tydeligt er der ovenstående billede, der kan bruges som tapet. I det vises katte og geder med to alternative sanser; katte er lodrette eller på hovedet, og geder ligger nedad eller opad.
Disse katte og geder etablerer en gentagen strukturel sekvens. For at bygge hele papiret ville det være tilstrækkeligt at reproducere enhedscellen over overfladen et tilstrækkeligt antal gange ved hjælp af translationelle bevægelser..
Mulige enhedsceller er repræsenteret af de blå, grønne og røde felter. Enhver af disse tre kunne bruges til at opnå rollen; men det er nødvendigt at flytte dem fantasifuldt langs overfladen for at finde ud af, om de gengiver den samme sekvens, der er observeret i billedet.
Startende med den røde boks, ville det forstås, at hvis tre søjler (af katte og geder) blev flyttet til venstre, ville to geder ikke længere vises i bunden, men kun en. Derfor vil det føre til en anden sekvens og kan ikke betragtes som en enhedscelle.
Mens de fantasifuldt flyttede de to kasser, blå og grøn, ville den samme sekvens af papiret opnås. Begge er enhedsceller; dog overholder den blå boks definitionen mere, da den er mindre end den grønne boks.
Artikelindeks
Dets egen definition, ud over det netop forklarede eksempel, tydeliggør flere af dens egenskaber:
-Hvis du bevæger dig i rummet, uanset retningen, får du det komplette faststof eller krystal. Dette skyldes, som de nævnes med katte og geder, de gengiver den strukturelle sekvens; som er lig med den rumlige fordeling af de gentagne enheder.
-De skal være så små som muligt (eller optage lidt volumen) sammenlignet med andre mulige celleindstillinger.
-De er normalt symmetriske. Desuden afspejles dens symmetri bogstaveligt i forbindelsens krystaller; hvis enhedens celle i et salt er kubisk, vil dets krystaller være kubiske. Der er imidlertid krystallinske strukturer, der er beskrevet med enhedsceller med forvrængede geometrier..
-De indeholder gentagne enheder, som kan erstattes af punkter, der igen udgør det, der er kendt som et gitter i tre dimensioner. I det foregående eksempel repræsenterer katte og geder gitterpunkterne set fra et højere plan; to dimensioner.
Enhedscellernes gentagne enheder eller gitterpunkter opretholder den samme andel af de faste partikler.
Hvis du tæller antallet af katte og geder i den blå boks, har du to katte og geder. Det samme sker med den grønne boks og med den røde boks også (selvom det allerede vides, at det ikke er en enhedscelle).
Antag for eksempel, at katte og geder er henholdsvis G- og C-atomer (en mærkelig dyresvejsning). Da forholdet mellem G og C er 2: 2 eller 1: 1 i den blå boks, kan det med sikkerhed forventes, at det faste stof har formlen GC (eller CG).
Når det faste stof præsenterer mere eller mindre kompakte strukturer, som det sker med salte, metaller, oxider, sulfider og legeringer, er der ikke i enhedscellerne hele gentagne enheder; der er dele eller dele af dem, der tilføjer op til en eller to enheder.
Dette er ikke tilfældet for GC. I så fald vil den blå boks "opdele" katte og geder i to (1 / 2G og 1 / 2C) eller fire (1 / 4G og 1 / 4C). I de næste afsnit vil det ses, at retikulære punkter i disse enhedsceller fordeles bekvemt på denne og andre måder..
Enhedscellerne i GC-eksemplet er todimensionale; dette gælder dog ikke rigtige modeller, der tager højde for alle tre dimensioner. Således omdannes kvadraterne eller parallelogrammerne til parallelepipeder. Nu giver udtrykket "celle" mere mening.
Dimensionerne på disse celler eller parallelepipedier afhænger af, hvor længe deres respektive sider og vinkler er..
I det nederste billede har du det nederste bageste hjørne af parallelepiped, sammensat af siderne til, b Y c, og vinklerne α, β og γ.
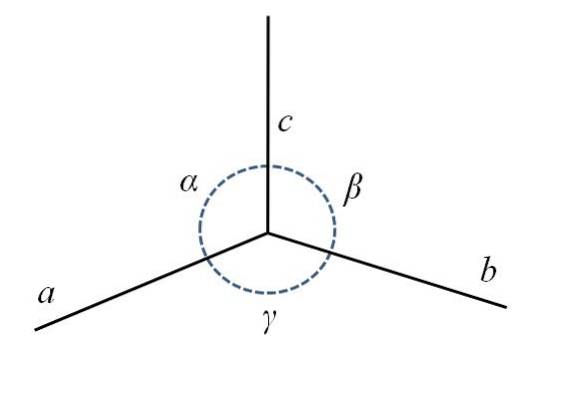
Som du kan se, til er lidt længere end b Y c. I midten er der en stiplet cirkel for at indikere vinklerne α, β og γ imellem ac, cb Y ba, henholdsvis. For hver enhedscelle har disse parametre konstante værdier og definerer dens symmetri og resten af krystallen..
Ved at anvende noget fantasi igen ville billedparametrene definere en terninglignende celle strakt ud på kanten. til. Således opstår enhedsceller med forskellige længder og vinkler på deres kanter, som også kan klassificeres i forskellige typer.
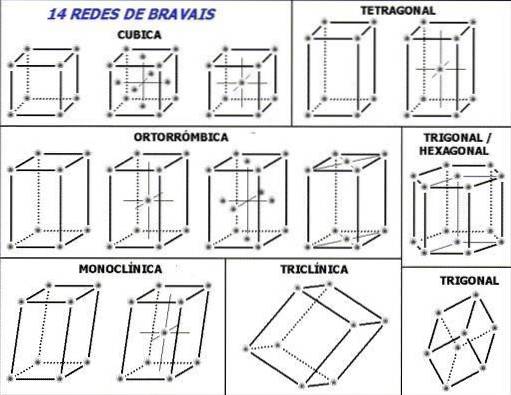
Bemærk til at begynde med i det øverste billede de stiplede linjer inden i enhedscellerne: de angiver den nedre bageste vinkel, som netop forklaret. Følgende spørgsmål kan stilles, hvor er gitterpunkterne eller gentagne enheder? Selvom de giver det forkerte indtryk af, at cellerne er tomme, ligger svaret ved deres hjørner.
Disse celler genereres eller vælges på en sådan måde, at de gentagne enheder (grålige punkter i billedet) er placeret ved deres hjørner. Afhængigt af værdierne af parametrene, der er oprettet i det foregående afsnit, konstant for hver enhedscelle, afledes syv krystalsystemer.
Hvert krystalsystem har sin egen enhedscelle; det andet definerer det første. I det øverste billede er der syv firkanter svarende til de syv krystalsystemer; eller på en lidt mere sammenfattet måde krystallinske netværk. Således svarer for eksempel en kubisk enhedscelle til et af krystalsystemerne, der definerer et kubisk krystalgitter.
Ifølge billedet er de krystallinske systemer eller netværk:
-Kubisk
-Tetragonal
-Orthorhombic
-Sekskantet
-Monoklinik
-Triclinic
-Trigonal
Og inden for disse krystallinske systemer opstår andre, der udgør de fjorten Bravais-netværk; at blandt alle de krystallinske netværk er de mest basale.
I en terning er alle dens sider og vinkler ens. Derfor gælder følgende i denne enhedscelle:
til = b = c
α = β = γ = 90º
Der er tre kubiske enhedsceller: enkle eller primitive, kropscentrerede (bcc) og ansigtscentrerede (fcc). Forskellene ligger i, hvordan punkterne fordeles (atomer, ioner eller molekyler) og i antallet af dem.
Hvilke af disse celler er de mest kompakte? Den, hvis volumen er mere optaget af punkter: den kubiske centreret på ansigterne. Bemærk, at hvis vi erstattede prikkerne med katte og geder fra begyndelsen, ville de ikke være begrænset til en enkelt celle; de ville høre hjemme og ville blive delt af flere. Igen ville det være dele af G eller C.
Hvis katte eller geder var ved hjørnerne, ville de deles af 8 enhedsceller; det vil sige, at hver celle ville have 1/8 af G eller C. Deltag eller forestil dig 8 kuber i to kolonner med to rækker hver for at visualisere det.
Hvis katte eller geder var i ansigterne, ville de kun deles af 2 enhedsceller. For at se det skal du bare sætte to terninger sammen.
På den anden side, hvis katten eller geden var i midten af terningen, ville de kun tilhøre en enkelt enhedscelle; Det samme sker med boksene i hovedbilledet, da konceptet blev behandlet.
Så sagde ovenstående inden for en simpel kubisk enhedscelle, vi har -en enhed eller gitterpunkt, da det har 8 hjørner (1/8 x 8 = 1). For den kubiske celle centreret i kroppen er der: 8 hjørner, som er lig med et atom, og et punkt eller en enhed i midten; derfor er der to enheder.
Og for den ansigtscentrerede kubiske celle er der: 8 hjørner (1) og seks ansigter, hvor halvdelen af hvert punkt eller enhed er delt (1/2 x 6 = 3); derfor besidder det fire enheder.
Lignende kommentarer kan fremsættes vedrørende enhedscellen til det tetragonale system. Dens strukturelle parametre er følgende:
til = b ≠ c
α = β = γ = 90º
Parametrene for den orthorhombiske celle er:
til ≠ b ≠ c
α = β = γ = 90º
Parametrene for den monokliniske celle er:
til ≠ b ≠ c
a = y = 90 °; β ≠ 90º
Parametrene for triclinic cellen er:
til ≠ b ≠ c
α ≠ β ≠ γ ≠ 90º
Parametrene for den sekskantede celle er:
til = b ≠ c
a = P = 90 °; γ ≠ 120º
Faktisk udgør cellen en tredjedel af et sekskantet prisme.
Og endelig er parametrene for den trigonale celle:
til = b = c
α = β = γ ≠ 90º
Endnu ingen kommentarer