
Tyngdepunktets egenskaber, beregning, eksempler
Det tyngdepunkt af en krop af målelig størrelse er det punkt, hvor dens vægt anses for at være anvendt. Det er derfor et af de grundlæggende begreber i Statics.
Den første tilgang i problemerne med elementærfysik består i at antage, at ethvert objekt opfører sig som en punktmasse, det vil sige, det har ingen dimensioner, og al massen er koncentreret i et enkelt punkt. Dette gælder for en kasse, en bil, en planet eller en subatomær partikel. Denne model er kendt som partikelmodel.

Dette er naturligvis en tilnærmelse, som fungerer meget godt til mange applikationer. Det er ikke en let opgave at overveje den individuelle adfærd for de tusinder og millioner af partikler, som ethvert objekt kan indeholde.
Imidlertid skal de reelle dimensioner af ting tages i betragtning, hvis der skal opnås resultater, der er tættere på virkeligheden. Da vi generelt er i nærheden af Jorden, er den stadigt tilstedeværende kraft på enhver krop netop vægten.
Artikelindeks
- 1 Overvejelser for at finde tyngdepunktet
- 2 Hvordan beregnes tyngdepunktet?
- 3 egenskaber
- 3.1 -Find tyngdepunktet for et legeme i statisk ligevægt
- 3.2 -Løst eksempel
- 4 Forskel fra massecenter
- 5 Eksempler på tyngdepunkt
- 5.1 Tyngdepunkt for uregelmæssige genstande
- 5.2 Balancering af objekter
- 6 Referencer
Overvejelser for at finde tyngdepunktet
Hvis der skal tages højde for kropsstørrelse, hvor specifikt skal der anvendes vægt? Når du har et vilkårligt kontinuerligt objekt, er dens vægt a distribueret kraft mellem hver af dets bestanddele.
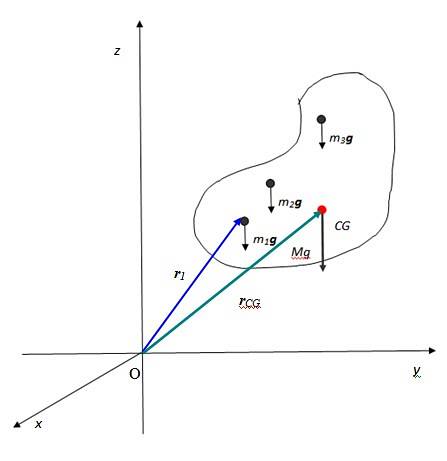
Lad disse partikler være m1, mto, m3... Hver af dem oplever sin tilsvarende tyngdekraft m1g, mtog, m3g…, alle sammen parallelle. Dette er tilfældet, da jordens tyngdefelt betragtes som konstant i langt de fleste tilfælde, da objekterne er små i forhold til planetens størrelse og er tæt på dens overflade..
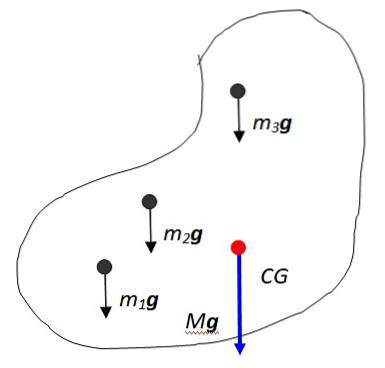
Vektorsummen af disse kræfter resulterer i genstandens vægt, anvendt på det punkt kaldet tyngdepunktet betegnet i figuren som CG, som derefter falder sammen med Massecenter. Massecentret er igen det punkt, hvor al massen kunne betragtes som koncentreret.
Den resulterende vægt har størrelse Mg hvor M er genstandens samlede masse, og selvfølgelig er den lodret lodret mod Jordens centrum. Summationsnotationen er nyttig til at udtrykke kroppens samlede masse:
Tyngdepunktet falder ikke altid sammen med et materielt punkt. For eksempel er ringens CG i dens geometriske centrum, hvor der ikke er nogen masse i sig selv. Alligevel skal du anvende vægten til dette nøjagtige punkt, hvis du vil analysere de kræfter, der virker på en ramme.
I de tilfælde, hvor objektet har en vilkårlig form, hvis det er homogent, kan dets massepunkt stadig beregnes ved at finde centroid eller tyngdepunktet for figuren.
Hvordan beregner man tyngdepunktet?
I princippet, hvis tyngdepunktet (CG) og massepunktet (cm) falder sammen, da tyngdefeltet er ensartet, kan cm beregnes og vægten påføres det.
Lad os overveje to tilfælde: den første er en, hvor massefordelingen er diskret; det vil sige, at hver masse, der udgør systemet, kan tælles og tildeles et nummer i, som det blev gjort i det foregående eksempel.
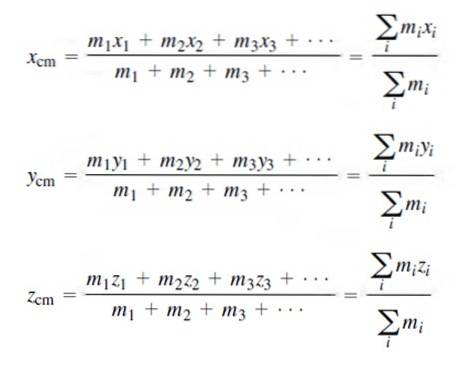
Koordinaterne for massecentret for en diskret massefordeling er:
Naturligvis er summen af alle masserne lig med den samlede masse af systemet M, som angivet ovenfor..
De tre ligninger reduceres til en kompakt form ved at overveje vektoren rcm eller placeringsvektor for massecentret:
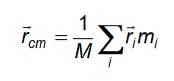
Og i tilfælde af en kontinuerlig massefordeling, hvor partiklerne har forskellig størrelse og ikke kan skelnes for at tælle dem, erstattes summen med en integral, der er lavet over det volumen, der optages af det pågældende objekt:
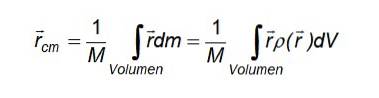
Hvor r er positionsvektoren for en differentiel masse dm og definitionen af massefylde er blevet brugt til at udtrykke massedifferentialet dm indeholdt i en volumenforskel dV:
Ejendomme
Nogle vigtige overvejelser omkring massecentret er som følger:
- Selvom der kræves et referencesystem for at etablere positionerne, afhænger massepunktet ikke af systemets valg, da det er en genstand for objektet.
- Når objektet har en akse eller et symmetriplan, er massecentret på den akse eller det plan. Udnyttelse af denne omstændighed sparer beregningstid.
- Alle eksterne kræfter, der virker på objektet, kan påføres massecentret. At holde styr på bevægelsen af dette punkt giver en global idé om objektets bevægelse og letter arbejdet med at studere dets adfærd..
-At finde tyngdepunktet for et legeme i statisk ligevægt
Antag, at du vil gøre kroppen i den foregående figur i statisk ligevægt, det vil sige, at den ikke oversættes eller roterer omkring en vilkårlig rotationsakse, der kan være O.

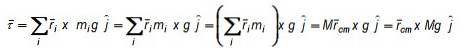
-Arbejdet eksempel
En tynd stang af ensartet materiale er 6 m lang og vejer 30 N. En 50 N vægt hænges i sin venstre ende og en 20 N vægt hænges i sin højre ende. Find: a) Størrelsen af den opadgående kraft, der er nødvendig for at opretholde balancen i stangen, b) Sætets tyngdepunkt.
Opløsning
Kraftdiagrammet er vist i den følgende figur. Stangens vægt påføres ved dens tyngdepunkt, som falder sammen med dens geometriske centrum. Den eneste dimension af stangen, der tages i betragtning, er dens længde, da udsagnet oplyser, at den er tynd.
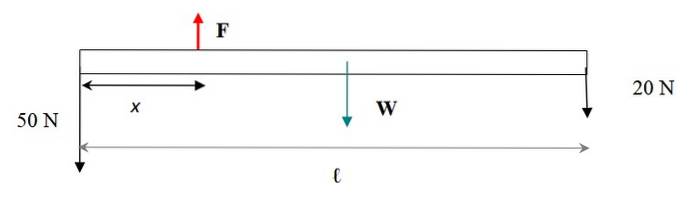
For at bar + vægtsystemet forbliver i translationel ligevægt, skal summen af kræfterne være nul. Kræfterne er lodrette, hvis vi overvejer op med tegn + og ned med tegn - så:
F- 50 - 20 - 30 N = 0
F = 100 N
Denne kraft garanterer den translationelle balance. Tager torsionsmomenterne for alle kræfterne i forhold til en akse, der passerer gennem den venstre ende af systemet og anvender definitionen:
t = r x F
Momenterne for alle disse kræfter omkring det valgte punkt er vinkelret på bjælkens plan:
tF = xF = 100x
tW = - (l / 2) mg = -3m. 30 N = -90 N.m
t1 = 0 (da 50 N-kraften passerer gennem den valgte rotationsakse og ikke udøver øjeblik)
tto = -lFto = 6 m. 20 N = -120 N.m
Derfor:
100 x -90 -120 N.m = 0
x = 2,10 m
Tyngdepunktet for søjlen + vægtsættet er placeret 2,10 meter fra den venstre ende af søjlen.
Forskel fra massecenter
Tyngdepunktet falder sammen med massepunktet som angivet, så længe jordens tyngdefelt er konstant, så alle punkter i objektet kan tages i betragtning. Jordens tyngdefelt er intet andet end den velkendte og velkendte værdi af g = 9,8 m / sto rettet lodret nedad.
Selvom værdien af g varierer med bredde og højde, påvirker disse normalt ikke de genstande, der er mest af tiden. Det ville være meget anderledes, hvis du overvejer en stor krop i nærheden af Jorden, for eksempel en asteroide, der er meget tæt på planeten.
Asteroiden har sit eget massepunkt, men tyngdepunktet behøver ikke længere være sammenfaldende med dette, da g ville sandsynligvis opleve betydelige variationer i størrelse i betragtning af asteroidens størrelse, og at vægten af hver partikel muligvis ikke er parallel.
En anden grundlæggende forskel er, at massepunktet findes uanset om der er en kraft kaldet vægt påført objektet eller ej. Det er en iboende egenskab ved objektet, der afslører for os, hvordan dens masse fordeles i forhold til dens geometri.
Massecentret eksisterer, uanset om der er anvendt vægt. Og det er placeret i samme position, selvom objektet bevæger sig til en anden planet, hvor tyngdefeltet er anderledes..
På den anden side er tyngdepunktet tydeligt knyttet til anvendelsen af vægt, som vi har set gennem de foregående afsnit..
Eksempler på tyngdepunkt
Tyngdepunkt for uregelmæssige genstande
Det er meget let at finde ud af, hvor tyngdepunktet for en uregelmæssig genstand som en kop er. For det første er den suspenderet fra ethvert punkt, og derfra tegnes en lodret linje (i figur 5 er det fuchsia-linjen i det venstre billede).
Derefter suspenderes det fra et andet punkt, og en ny lodret tegnes (turkis linje i det rigtige billede). Skæringspunktet mellem begge linjer er bægerets tyngdepunkt.

Balancering af objekter
Lad os analysere stabiliteten af en lastbil, der kører på vejen. Når tyngdepunktet er over truckens bund, vælter trucken ikke. Billedet til venstre er den mest stabile position.
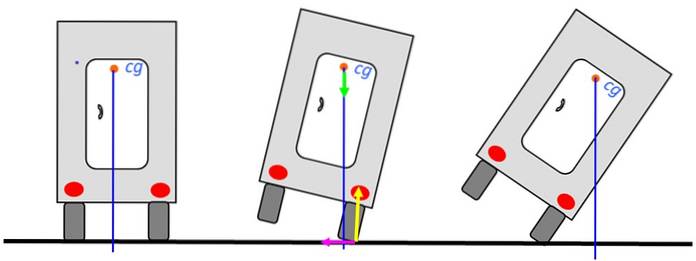
Selv når trucken vippes mod højre, vil den være i stand til at vende tilbage til en stabil ligevægtsposition, som i den midterste tegning, da lodret stadig passerer gennem basen. Men når denne linje passerer udenfor, vælter lastbilen.
Diagrammet viser kræfterne ved omdrejningspunktet: normal i gul, vægt i grønt og statisk gnidning til venstre i fuchsia. Normal og friktion påføres rotationsaksen, så de ikke udøver moment. Derfor bidrager de ikke til at vælte trucken.
Vægten forbliver, hvilket udøver et moment, heldigvis mod uret, og som har tendens til at bringe trucken tilbage i sin ligevægt. Bemærk, at den lodrette linje passerer gennem støttefladen, som er dækket.
Når trucken er i den yderste højre position, ændres vægtens drejningsmoment til uret. Kan ikke imødegås en anden gang, vil trucken vælte.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6.… Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Fysisk. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Grundlæggende fysik. Pearson. 146-155.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.340-346.



Endnu ingen kommentarer