Hvordan finder man vinklen på en trekant?

Der er flere måder at beregne siderne og vinklerne på en trekant. Disse afhænger af den type trekant, du arbejder med.

I denne mulighed vil det blive vist, hvordan man beregner siderne og vinklerne på en højre trekant, forudsat at visse data i trekanten med kendt.

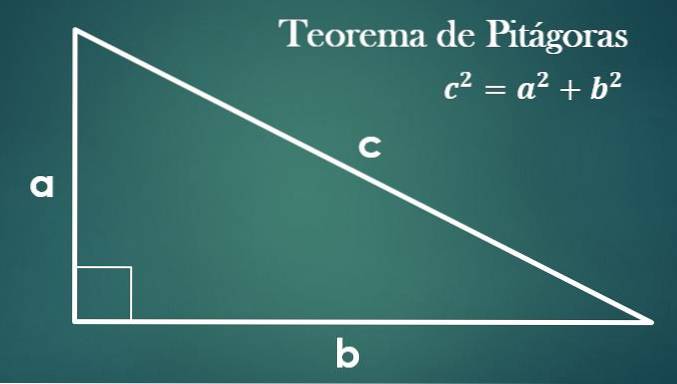
De elementer, der vil blive brugt, er:

- Pythagoras sætning

Givet en højre trekant med ben "a", "b" og hypotenus "c", er det rigtigt, at "c² = a² + b²".

- Område af en trekant

Formlen til beregning af arealet af en hvilken som helst trekant er A = (b × h) / 2, hvor “b” er længden af ​​basen og “h” er længden af ​​højden.

- Vinkler af en trekant

Summen af ​​de tre indvendige vinkler i en trekant er 180º.

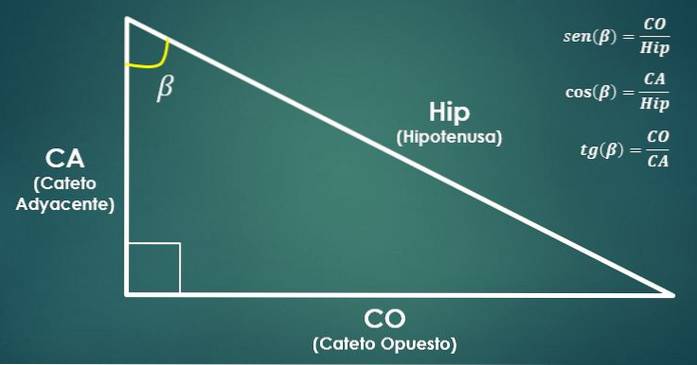
- Trigonometriske funktioner:

Overvej en ret trekant. Derefter defineres de trigonometriske funktioner sinus, cosinus og tangens for vinklen beta (β) som følger:

sin (β) = CO / Hip, cos (β) = CA / Hip og tan (β) = CO / CA.

Sådan finder du siderne og vinklerne på en ret trekant?

Givet en ret trekant ABC, kan følgende situationer forekomme:

1- De to ben er kendte

Hvis ben “a” måler 3 cm og ben “b” måler 4 cm, bruges den pythagoriske sætning til at beregne værdien af ​​“c”. Ved at erstatte værdierne for "a" og "b" opnår vi, at c² = 25 cm², hvilket betyder, at c = 5 cm.

Hvis vinklen β er modsat benet "b", er sin (β) = 4/5. Ved at anvende sinusens inverse funktion opnår vi i denne sidste ligestilling, at β = 53,13º. To indre vinkler i trekanten er allerede kendt.

Lad θ være den vinkel, der stadig er kendt, så 90º + 53,13º + θ = 180º, hvorfra vi opnår at θ = 36,87º.

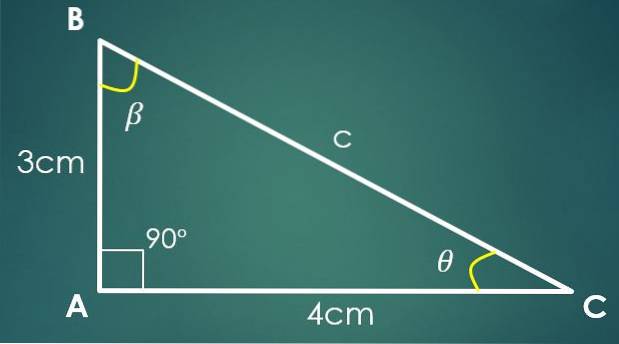
I dette tilfælde er det ikke nødvendigt, at de kendte sider er de to ben, det vigtige er at kende værdien af ​​to sider.

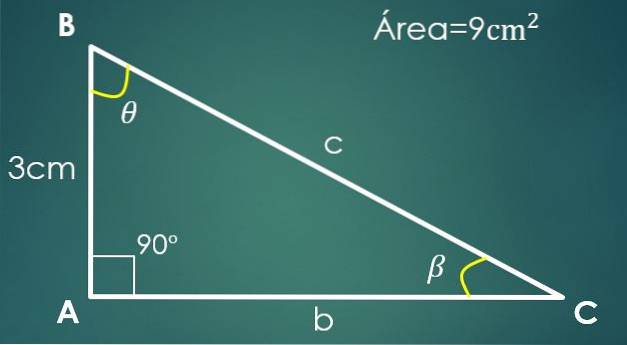
2- Et ben er kendt og området

Lad a = 3 cm være det kendte ben og A = 9 cm² arealet af trekanten.

I en højre trekant kan det ene ben betragtes som basen og det andet som højden (da de er vinkelrette).

Antag at “a” er basen, derfor er 9 = (3 × h) / 2, hvorfra vi får ud af, at det andet ben er 6 cm. For at beregne hypotenusen skal du fortsætte som i det forrige tilfælde, og vi får, at c = √45 cm.

Hvis vinklen β er modsat benet “a”, så er sin (β) = 3 / √45. Løsning for β opnås, at dens værdi er 26,57º. Vi behøver kun at kende værdien af ​​den tredje vinkel θ.

Det er tilfreds med, at 90º + 26,57º + θ = 180º, hvorfra det konkluderes, at θ = 63,43º.

3- En vinkel og et ben er kendt

Lad β = 45º være den kendte vinkel og a = 3 cm det kendte ben, hvor ben “a” er modsat vinkel β. Ved hjælp af tangensformlen opnår vi, at tg (45º) = 3 / CA, hvorfra det følger, at CA = 3 cm.

Ved hjælp af Pythagoras sætning opnås det at c² = 18 cm², det vil sige c = 3√2 cm.

Det vides, at en vinkel måler 90º, og at β måler 45º, herfra konkluderes det, at den tredje vinkel måler 45º.

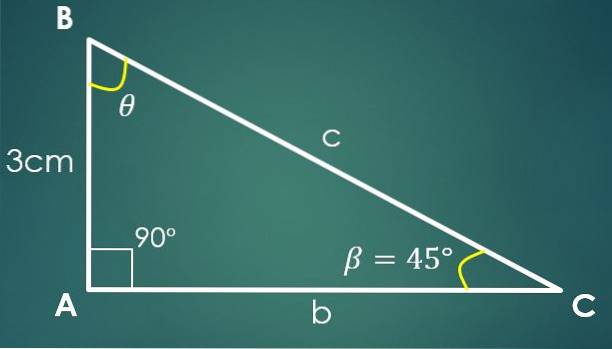
I dette tilfælde behøver den kendte side ikke at være et ben, det kan være en af ​​de tre sider af trekanten.

Referencer

1. Landaverde, F. d. (1997). Geometri (Genudskrivning red.). Fremskridt.
2. Leake, D. (2006). Trekanter (illustreret udgave). Heinemann-Raintree.
3. Pérez, C. D. (2006). Forberegning. Pearson Uddannelse.
4. Ruiz, Á., Og Barrantes, H. (2006). Geometrier. CR-teknologi.
5. Sullivan, M. (1997). Forberegning. Pearson Uddannelse.
6. Sullivan, M. (1997). Trigonometri og analytisk geometri. Pearson Uddannelse.