Det korrelationskoefficient i statistik er det en indikator, der måler tendensen for to kvantitative variabler X og Y til at have et lineært eller proportionalt forhold mellem dem.
Generelt er parene af variabler X og Y to karakteristika for den samme population. For eksempel kan X være en persons højde og Y sin vægt..
I dette tilfælde vil korrelationskoefficienten indikere, om der er en tendens til et forholdsmæssigt forhold mellem højde og vægt i en given population..
Pearsons lineære korrelationskoefficient er angivet med brevet r små bogstaver, og dens minimums- og maksimumværdier er henholdsvis -1 og +1.
En værdi r = +1 vil indikere, at sæt par (X, Y) er perfekt justeret, og at når X vokser, vil Y vokse i samme forhold. På den anden side, hvis det skete, at r = -1, ville parret også være perfekt justeret, men i dette tilfælde når X øges, falder Y i samme forhold.
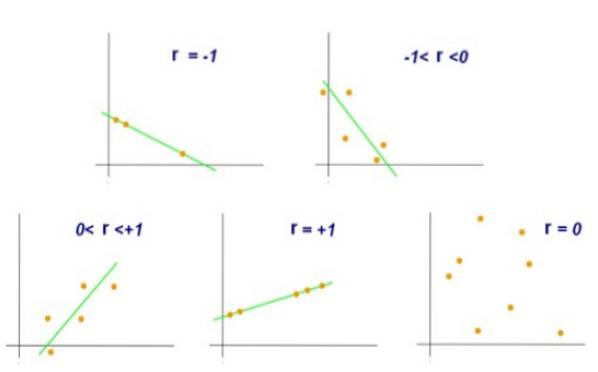
På den anden side vil en værdi på r = 0 indikere, at der ikke er nogen lineær sammenhæng mellem variablerne X og Y. Mens en værdi på r = +0,8 vil indikere, at parene (X, Y) har tendens til at klynges på den ene side og en anden af en bestemt straight.
Formlen til beregning af korrelationskoefficienten r er som følger:
Den lineære korrelationskoefficient er en statistisk størrelse, der findes i videnskabelige regnemaskiner, de fleste regneark og statistiske programmer..
Det er dog praktisk at vide, hvordan formlen, der definerer den, anvendes, og for dette vises en detaljeret beregning udført på et lille datasæt.
Og som det blev sagt i det foregående afsnit, er korrelationskoefficienten kovariansen Sxy divideret med produktet af standardafvigelsen Sx for variablerne X og Sy for variablen Y.
Kovariansen Sxy er:
Sxy = [Σ (Xi -
Hvor summen går fra 1 til N par af data (Xi, Yi).
For sin del er standardafvigelsen for variablen X kvadratroden af variansen af datasættet Xi, med i fra 1 til N:
Sx = √ [Σ (Xi -
Tilsvarende er standardafvigelsen for variabel Y kvadratroden af variansen af datasættet Yi, med i fra 1 til N:
Sy = √ [Σ (Yi -
For at vise detaljeret, hvordan man beregner korrelationskoefficienten, tager vi følgende sæt med fire par data
(X, Y): (1, 1); (2. 3); (3, 6) og (4, 7).
Først beregner vi det aritmetiske gennemsnit for X og Y som følger:
Derefter beregnes de resterende parametre:
Sxy = [(1 - 2,5) (1 - 4,25) + (2 - 2,5) (3 - 4,25) + (3 - 2,5) (6 - 4,25) +…. ... (4 - 2,5) (7 - 4,25) ] / (4-1)
Sxy = [(-1,5) (- 3,25) + (-0,5) (- 1,25) + (0,5) (1,75) +… .
…. (1.5) (2.75)] / (3) = 10.5 / 3 = 3.5
Sx = √ [(-1,5)to + (-0,5)to + (0,5)to + (1.5)to) / (4-1)] = √ [5/3] = 1.29
Sx = √ [(-3,25)to + (-1,25)to + (1,75)to + (2,75)to) / (4-1)] =
√ [22,75 / 3] = 2,75
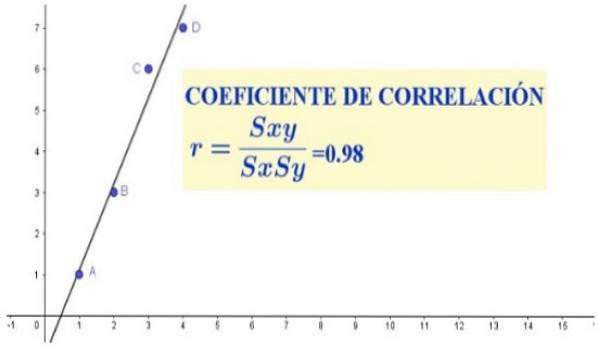
r = 3,5 / (1,29 * 2,75) = 0,98
I datasættet fra det foregående tilfælde observeres en stærk lineær korrelation mellem variablerne X og Y, som manifesteres både i spredningsdiagrammet (vist i figur 1) og i korrelationskoefficienten, som gav en værdi, der var tæt på enhed.
I det omfang korrelationskoefficienten er tættere på 1 eller -1, jo mere mening giver det at tilpasse dataene til en linje, resultatet af lineær regression..
Den lineære regressionslinie fås fra Metode med mindste firkanter. hvor parametrene for regressionslinjen opnås ved at minimere summen af kvadratet af forskellen mellem den estimerede Y-værdi og Yi for N-dataene.
På den anden side er parametrene a og b for regressionslinien y = a + bx, opnået ved metoden med mindste kvadrat,:
* b = Sxy / (Sxto) Til skråningen
* a =
Husk, at Sxy er den ovenfor definerede kovarians og Sxto er variansen eller kvadratet af standardafvigelsen defineret ovenfor.
Korrelationskoefficienten bruges til at bestemme, om der er en lineær korrelation mellem to variabler. Det kan anvendes, når de variabler, der skal undersøges, er kvantitative, og det antages desuden, at de følger en normal typefordeling..
Vi har et illustrativt eksempel nedenfor: et mål for fedmegraden er kropsmasseindekset, der opnås ved at dividere en persons vægt i kg med den samme kvadrathøjde i enheder kvadratmeter.
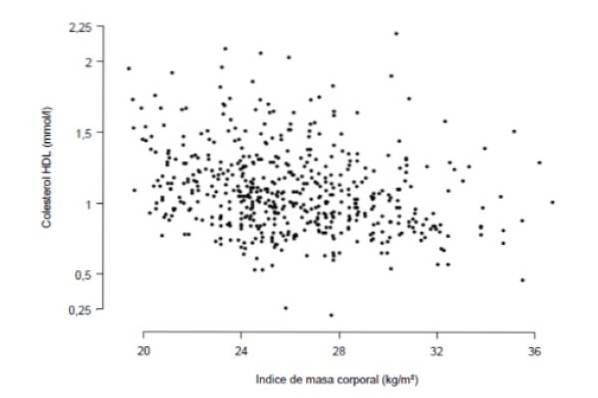
Du vil vide, om der er en stærk sammenhæng mellem body mass index og koncentrationen af HDL-kolesterol i blodet målt i millimol per liter. Til dette formål er der udført en undersøgelse med 533 personer, der er opsummeret i den følgende graf, hvor hvert punkt repræsenterer dataene for en person.
Omhyggelig observation af grafen viser, at der er en vis lineær tendens (ikke særlig markeret) mellem koncentrationen af HDL-kolesterol og body mass index. Det kvantitative mål for denne tendens er korrelationskoefficienten, som i dette tilfælde viste sig at være r = -0,276.
Endnu ingen kommentarer