Det bestemmelseskoefficient er et tal mellem 0 og 1, der repræsenterer den brøkdel af punkterne (X, Y), der følger regressionens pasform for et datasæt med to variabler.
Det er også kendt som godhed af pasform og er betegnet med Rto. For at beregne det tages kvotienten mellem variansen af data Ŷi estimeret af regressionsmodellen og variansen af data Yi svarende til hver Xi af dataene.
Rto = Sŷ / Sy
Hvis 100% af dataene er på linjen med regressionsfunktionen, vil bestemmelseskoefficienten være 1.
Tværtimod, hvis koefficienten R for et datasæt og en bestemt justeringsfunktionto viser sig at være lig med 0,5, så kan det siges, at pasformen er 50% tilfredsstillende eller god.
Tilsvarende når regressionsmodellen returnerer værdier på Rto lavere end 0,5, indikerer dette, at den valgte justeringsfunktion ikke tilpasser sig tilfredsstillende til dataene, derfor er det nødvendigt at kigge efter en anden justeringsfunktion.
Og når den kovarians eller den korrelationskoefficient har en tendens til nul, så er variablerne X og Y i dataene ikke relaterede, og derfor er Rto vil også have en tendens til nul.
Artikelindeks
I det forrige afsnit blev det sagt, at bestemmelseskoefficienten beregnes ved at finde kvotienten mellem varianserne:
-Estimeret af regressionsfunktionen for variablen Y
-Det for variablen Yi, der svarer til hver af variablen Xi for N-dataparene.
Angivet matematisk ser det sådan ud:
Rto = Sŷ / Sy
Fra denne formel følger det, at Rto repræsenterer variansandelen forklaret af regressionsmodellen. Alternativt kan R beregnesto ved hjælp af følgende formel, svarende til den foregående:
Rto = 1 - (Sε / Sy)
Hvor Sε repræsenterer variansen af residualerne εi = Ŷi - Yi, mens Sy er variansen af datasættet Yi-værdier. For at bestemme Ŷi anvendes regressionsfunktionen, hvilket betyder at bekræfte, at Ŷi = f (Xi).
Variansen af datasættet Yi med i fra 1 til N beregnes som følger:
Sy = [Σ (Yi -
Og fortsæt derefter på en lignende måde for Sŷ eller for Sε.
For at vise detaljerne i, hvordan beregningen af bestemmelseskoefficient vi tager følgende sæt med fire par data:
(X, Y): (1, 1); (2. 3); (3, 6) og (4, 7).
Der foreslås en lineær regressionstilpasning til dette datasæt, som opnås ved hjælp af metoden med mindst kvadrat:
f (x) = 2,1 x - 1
Ved anvendelse af denne justeringsfunktion opnås momentene:
(X, Ŷ): (1, 1.1); (2, 3,2); (3, 5.3) og (4, 7.4).
Derefter beregner vi det aritmetiske gennemsnit for X og Y:
Varians Sy
Sy = [(1 - 4,25)to + (3 - 4,25)to + (6 - 4,25)to +….…. (7 - 4.25)to] / (4-1) =
= [(-3,25)to+ (-1,25)to + (1,75)to + (2,75)to) / (3)] = 7.583
Varians Sŷ
Sŷ = [(1,1 - 4,25)to + (3,2 - 4,25)to + (5.3 - 4.25)to +….…. (7.4 - 4.25)to] / (4-1) =
= [(-3,25)to + (-1,25)to + (1,75)to + (2,75)to) / (3)] = 7,35
Bestemmelseskoefficient Rto
Rto = S1 / Sy = 7,35 / 7,58 = 0,97
Bestemmelseskoefficienten for det illustrative tilfælde, der blev betragtet i det forrige segment, viste sig at være 0,98. Med andre ord, den lineære justering gennem funktionen:
f (x) = 2,1 x - 1
Det er 98% pålideligt til at forklare de data, hvormed det blev opnået ved hjælp af metoden med mindst kvadrat..
Ud over bestemmelseskoefficienten er der lineær korrelationskoefficient eller også kendt som Pearsons koefficient. Denne koefficient, betegnet som r, beregnes ved hjælp af følgende forhold:
r = Sxy / (Sx Sy)
Her repræsenterer tælleren kovariansen mellem variablerne X og Y, mens nævneren er produktet af standardafvigelsen for variablen X og standardafvigelsen for variablen Y.
Pearsons koefficient kan tage værdier mellem -1 og +1. Når denne koefficient har en tendens til +1, er der en direkte lineær korrelation mellem X og Y. Hvis den i stedet har tendens til -1, er der en lineær korrelation, men når X stiger, falder Y. Endelig er det tæt på 0, der er ingen sammenhæng mellem de to variabler.
Det skal bemærkes, at bestemmelseskoefficienten falder sammen med Pearson-koefficientens firkant, kun når den første er beregnet ud fra en lineær tilpasning, men denne lighed er ikke gyldig for andre ikke-lineære fittings..
En gruppe gymnasieelever satte sig for at bestemme en empirisk lov for pendulets periode som en funktion af dens længde. For at nå dette mål udfører de en række målinger, hvor de måler tiden for en pendelsvingning i forskellige længder og opnår følgende værdier:
| Længde (m) | Periode (r) |
|---|---|
| 0,1 | 0,6 |
| 0,4 | 1.31 |
| 0,7 | 1,78 |
| 1 | 1,93 |
| 1.3 | 2.19 |
| 1.6 | 2.66 |
| 1.9 | 2,77 |
| 3 | 3,62 |
Det anmodes om at lave et spredningsdiagram over dataene og udføre en lineær tilpasning gennem regression. Vis også regressionsligningen og dens bestemmelseskoefficient.
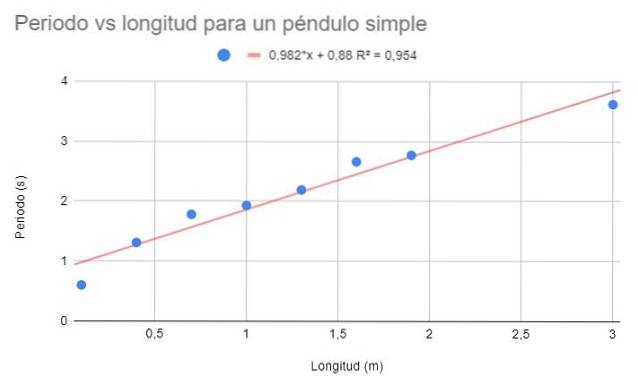
En ret høj bestemmelseskoefficient kan observeres (95%), så man kunne tro, at den lineære pasform er optimal. Men hvis punkterne ses sammen, ser det ud til at de har en tendens til at kurve nedad. Denne detalje overvejes ikke i den lineære model.
For de samme data i eksempel 1, lav et spredningsdiagram over dataene. I modsætning til eksempel 1 anmodes ved denne lejlighed om en regressionsjustering ved hjælp af en potentiel funktion.
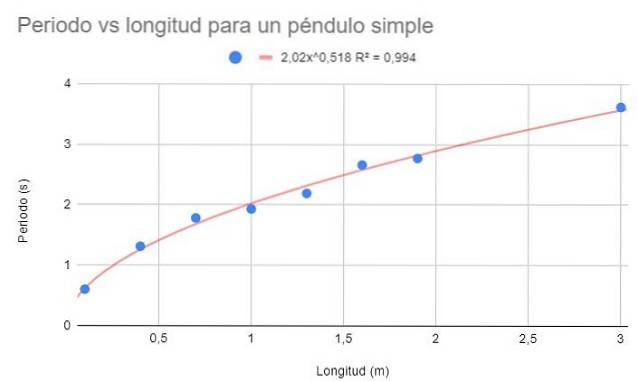
Vis også tilpasningsfunktionen og dens bestemmelseskoefficient Rto.
Den potentielle funktion er af formen f (x) = AxB, hvor A og B er konstanter, der bestemmes ved metoden med mindste kvadrat.
Den foregående figur viser den potentielle funktion og dens parametre såvel som bestemmelseskoefficienten med en meget høj værdi på 99%. Bemærk, at dataene følger trendlinjens krumning.
Brug de samme data fra eksempel 1 og eksempel 2, og udfør en anden grad polynomial tilpasning. Vis graf, polynomium for tilpasning og bestemmelseskoefficient Rto korrespondent.
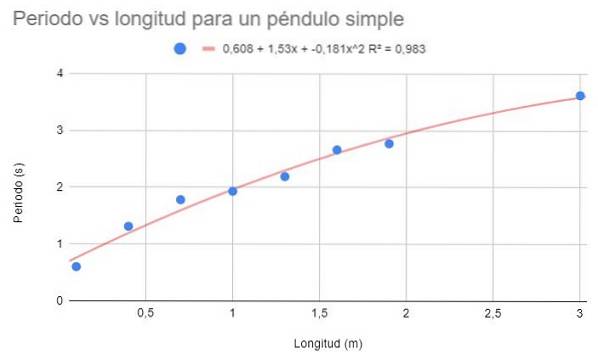
Med andengrads polynomial tilpasning kan du se en trendlinie, der passer godt til krumningen af dataene. Også bestemmelseskoefficienten er over den lineære tilpasning og under den potentielle tilpasning..
Af de tre viste tilpasninger er den med den højeste bestemmelseskoefficient den potentielle tilpasning (eksempel 2).
Den potentielle tilpasning falder sammen med den fysiske teori om pendulet, som som kendt fastslår, at pendulets periode er proportional med kvadratroden af dens længde, og proportionalitetskonstanten er 2π / √g hvor g er accelerationen tyngdekraft.
Denne type potentielle tilpasning har ikke kun den højeste bestemmelseskoefficient, men eksponenten og proportionalitetskonstanten matcher den fysiske model..
-Regressionstilpasning bestemmer parametrene for den funktion, der er beregnet til at forklare dataene ved hjælp af metoden med mindst kvadrat. Denne metode består i at minimere summen af den kvadratiske forskel mellem Y-værdien for justering og Yi-værdien af dataene for Xi-værdierne for dataene. Dette bestemmer parametrene for justeringsfunktionen.
-Som vi har set er den mest almindelige justeringsfunktion linjen, men den er ikke den eneste, da justeringerne også kan være polynomiske, potentielle, eksponentielle, logaritmiske og andre..
-Under alle omstændigheder afhænger bestemmelseskoefficienten af dataene og typen af pasform og er en indikation af godheden af den anvendte pasform..
-Endelig indikerer koefficienten for bestemmelse procentdelen af den samlede variabilitet mellem Y-værdien af dataene i forhold til Ŷ-værdien af fit for den givne X.
Endnu ingen kommentarer