
Bevaring af det lineære momentum-princip, eksempler, øvelser.
Det bevarelse af lineært momentum af et legeme fastslår, at produktet af dets masse og dets hastighedsvektor er en konstant størrelse, når kroppen er fri for interaktion med andre legemer og med den hastighed, der måles i forhold til en fast eller ikke-accelereret referenceramme.
Når du har flere kroppe, der kun interagerer med hinanden, men ikke med det eksterne miljø, så er lineært momentum af sættet forbliver også konstant over tid.

Det lineære momentum, momentum eller simpelthen momentum, er betegnet med brevet s y er en vektormængde:
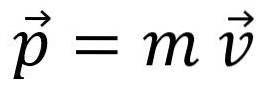
Momentum er ikke det samme som hastighed, selvom forholdet er indlysende: For eksempel har en lastbil, der kører 20 km / t, mere momentum end en cykel, der bevæger sig med samme hastighed.
For at et legemers lineære momentum skal ændre sig, skal en ekstern nettokraft virke på det, ellers forbliver det konstant. Også det lineære øjeblik P af et system dannet af n-kroppe er vektorsummen af de enkelte øjeblikke:
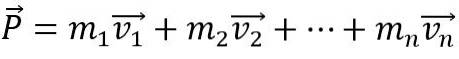
Artikelindeks
- 1 Princippet om bevarelse af lineært momentum
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 3 applikationer
- 3.1 Send i rummet
- 3.2 Dagligt liv
- 4 Øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Princippet om bevarelse af lineært momentum
I et kraftfrit legeme (eller et, hvor alle kræfterne på det annullerer) sker det, at det lineære øjeblik forbliver konstant.
Det samme sker i et system dannet af flere legemer, der kun interagerer med hinanden, men ikke med det ydre miljø: systemets samlede lineære momentum forbliver fast under udviklingen af helhedens bevægelse..
Dette bevarelsesprincip er angivet som følger:
Det samlede momentum for et sæt n-kroppe, der kun interagerer med hinanden, men ikke med det eksterne miljø, er en uforanderlig mængde i tid.
Og matematisk udtrykkes det som følger:
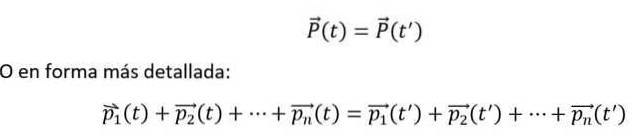
Ovenstående lighed er opfyldt, hvis og kun hvis n-kroppe interagerer med hinanden, men ikke med det ydre miljø. Desuden skal enkelte øjeblikke altid måles i forhold til en inerti-referenceramme..
Eksempler
Eksempel 1

To astronauter i rummet holder hænder og holdes i en fast position i forhold til rumfartøjet. Men hvis de skubber hinanden, begynder de at adskille sig i modsatte retninger, set fra skibet..
I dette tilfælde, da interaktionen mellem astronauterne kun er mellem dem gennem deres hænders kontaktkraft, er det samlede momentum efter skubning stadig den oprindelige værdi i forhold til rumfartøjet. Det vil sige total momentum 0.
Imidlertid ændrede hver astronauts momentum sig. Oprindeligt havde hver et 0-lineært øjeblik i forhold til skibet, men efter at være blevet skubbet, kommer man ud i den ene retning og den anden i den modsatte retning med ikke-nul lineære øjeblikke af samme størrelse og modsatte retninger..
Når de individuelle øjeblikke tilføjes vektorielt, opnås således det oprindelige samlede momentum som et resultat, som er nul.
På den anden side indikerer bevarelsen af momentumængden, at astronauten med den laveste masse er den, der bevæger sig hurtigere i forhold til rumfartøjet. Men resultatet af at multiplicere dens masse med dens hastighed er lig med det produkt, der opnås ved at multiplicere massen af den anden med hastigheden af den anden.
Eksempel 2
En hvalp er på en flydende platform i en rolig sø, og hans ejer holder øje med ham fra en dok. I starten hviler både platformen og hvalpen, men når hvalpen vil komme tættere på ejeren, bevæger platformen sig væk fra kajen.
Forklaringen på denne observation ligger netop i princippet om bevarelse af mængden af lineært momentum. Systemet består af hvalpen og platformen.
Hvalpen kan gå på platformen takket være friktionskraften mellem benene og overfladen, i dette tilfælde er friktionskraften en intern interaktionskraft mellem den og platformen.
Det hele er et isoleret system, da platformen kan bevæge sig vandret over søen, fri for enhver modstand mod bevægelse. På den anden side er alle kræfter i lodret retning afbalanceret og kompenseret, og helheden har ingen bevægelse i den retning..
Derfor er i denne situation alle hypoteser opfyldt, så princippet om bevarelse af lineært momentum gælder.
Eksempel 3

En eskimo er fanget i midten af en frossen sø, isen er så glat, at uanset hvor hårdt han prøver, glider eskimoen og forbliver altid på samme sted.
Den eneste mulige måde for eskimoerne at komme ud af søen er, at han kaster i den modsatte retning, som han vil flytte en tung genstand, som han bærer i sin rygsæk (forudsat at han har en).
Ansøgninger
Send i rummet

Bevaring af lineært momentum anvendes til at drive en raket ind i det ydre rum, hvor der ikke er nogen eksterne kræfter. I dette tilfælde opnås skibets impuls ved at uddrive gasser med høj hastighed, så raketten kan bevæge sig i den modsatte retning, som de blev skubbet ud til..
Hvis skibet oprindeligt er i ro, når det brænder og uddriver brændstof, forekommer udvisningens kraft mod selve skibet. Det er en intern kraft mellem gasserne og skibet. Der er ingen eksterne kræfter, og derfor gælder bevarelsen af det lineære momentum.
Da gassernes lineære momentum er det samme og modsat skibets, formår det at komme ud af hvile, og ved at fortsætte med at uddrive gasser øger det dets bevægelsesmængde og dermed dets hastighed.
Daglig liv

Et andet tilfælde af anvendelse af bevarelsen af lineært momentum i hverdagen er at køre et søm ind i træet ved at drage fordel af mængden af hammerens bevægelse eller momentum..
Man kunne hævde, at i dette tilfælde gælder princippet ikke, fordi der er en ekstern kraft: træets modstand mod neglen..
I kontaktøjeblikket er den kraft, som hammeren påfører neglen, en intern kraft (mellem systemet, der er sømmen og hammeren), meget større end den modstand, som træet modsætter sig, og derfor er sidstnævnte ubetydelig.
Hele hammerens momentum, der er ret stort på grund af sin store masse og hastighed, overføres til neglen lige efter sammenstødet. Bemærk, at hele øjeblikket, men ikke al den kinetiske energi fra hammeren overføres, da en del af dette omdannes til termisk energi i neglen og i hammeren, hvilket hæver deres temperatur efter stødet.
Uddannelse
Øvelse 1
Astronauterne Andrew og Berenice er uden for rumstationen og holder begge hænder og i ro i forhold til stationen. De drives ved at skubbe hænderne på den ene mod den anden, og de frigives. Hvis Andrew, 70 kg masse, bevæger sig med 1 m / s i forhold til stationen, hvad er hastigheden på Berenice med 49 kg masse?
Opløsning
I dette tilfælde gælder hypoteserne om bevarelse af lineær momentum klart, da der ikke er nogen eksterne kræfter i det ydre rum. Kraften, hvormed begge astronauter skubber deres hænder, er en intern styrke.
Antag, at Andrews masse er Mtil og Berenice Mb. Tilsvarende er hastighederne for begge efter impulsen Vtil for Andrew og Vb til Berenice. Så gælder bevarelsen af lineært momentum som dette:
Mtil∙0 + Mb∙0 = Mtil∙Vtil+ Mb∙Vb
Løsning for Berenices hastighed har vi:
Vb = - (Mtil / Mb) ∙ Vtil
Placering af de numeriske værdier:
Vb = - (70/49) ∙ (1m / s) eller = -1,43m / s eller
Det vil sige, Berenice bevæger sig med en hastighed på 1,43 m / s i den modsatte retning af Andrew.
Øvelse 2

En hvalp med en masse på 5 kg hviler på en 15 kg platform, der flyder, også i ro, på en stille sø. Hvis hvalpen begynder at gå på platformen med en hastighed på 0,5 m / s i forhold til den. Hvor hurtigt vil hvalpen og platformen have i forhold til en observatør fastgjort til jorden??
Opløsning
Træghetsreferencesystemet tages som kajen, hvor hvalpens ejer er. Oprindeligt hviler både hvalpen og den flydende platform med hensyn til kajen..
Når hvalpen beslutter sig for hurtigt at gå mod ejeren v ' i forhold til platformen, bevæger platformen sig væk fra molen med hastighed +V. Hvalpens hastighed i forhold til fjederen opnås ved hjælp af vektorsummen af dens hastighed i forhold til platformen plus platformens hastighed, og vi betegner det med:
v = -v'' + V
Da vandets modstand mod platformens bevægelse praktisk talt er nul på grund af dets lave hastighed, kan det siges, at systemet består af hvalpen + platformen er et isoleret system, og princippet om bevarelse af lineært momentum gælder:
0 = m ∙ v + M ∙ V
Husk at v = v '+ V vi har:
0 = -m ∙ v '+ m ∙ v + M ∙ V
Det vil sige: m ∙ v '= (m + M) ∙ V
Derfor er V = [m / (m + M)] v 'og v = - (M / m) V = - [M / (m + M)] v'
Udskiftning af de numeriske værdier, vi har:
V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s
Dette er den hastighed, hvormed platformen bevæger sig væk fra kajen.
V = - (15/20) ∙ 0,5 m / s = -0,375 m / s
Og det er den hastighed hvormed hvalpen nærmer sig kajen.
Referencer
- Duke University. Partikelsystemer. Gendannet fra: webhome.phy.duke.edu.
- Rex, A. 2011. Grundlæggende fysik. Pearson.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
- .


Endnu ingen kommentarer