Det Boltzmann konstant er den værdi, der relaterer den gennemsnitlige kinetiske energi i et termodynamisk system eller et objekt med dets absolutte temperatur. Selvom de ofte er forvirrede, er temperatur og energi ikke det samme koncept.
Temperatur er et mål for energi, men ikke energi i sig selv. Med Boltzmanns konstant er de knyttet til hinanden på følgende måde:
OGc = (3/2) kB T
Denne ligning er gyldig for et monatomisk ideal gasmolekyle m, hvor OGc er dens kinetiske energi givet i Joule, kB er Boltzmanns konstant og T er den absolutte temperatur i Kelvin.
Når temperaturen stiger, stiger den gennemsnitlige kinetiske energi pr. Molekyle stof også, som det forventes at ske. Og det modsatte sker, når temperaturen falder og er i stand til at nå det punkt, hvor den lavest mulige temperatur eller absolutte nul nås, hvis al bevægelse ophører..
Når vi taler om gennemsnitlig kinetisk energi, er det nødvendigt at huske, at kinetisk energi er forbundet med bevægelse. Og partikler kan bevæge sig på mange måder, såsom at bevæge sig, rotere eller vibrere. Selvfølgelig vil ikke alle gøre det på samme måde, og da de er utallige, tages gennemsnittet for at karakterisere systemet..
Nogle energitilstande er mere sandsynlige end andre. Dette koncept er af radikal betydning i termodynamikken. Den energi, der betragtes i ovenstående ligning, er translationel kinetisk energi. Sandsynligheden for stater og dets forhold til Boltzmanns konstant vil blive drøftet lidt senere..
I 2018 blev Kelvin omdefineret og dermed Boltzmann-konstanten, som i det internationale system er ca. 1.380649 x 10-2. 3 J. K-1. Meget mere præcision kan opnås for Boltzmann-konstanten, som er blevet bestemt i adskillige laboratorier rundt om i verden, ved forskellige metoder..
Artikelindeks
Den berømte konstant skylder sit navn til den Wien-fødte fysiker Ludwig Boltzmann (1844-1906), der dedikerede sit liv som videnskabsmand til undersøgelse af systemers statistiske opførsel med mange partikler set fra Newtons mekanikers synspunkt..
Selvom eksistensen af atom i dag er universelt accepteret, var det i det nittende århundrede troen på, om atomet virkelig eksisterede eller var et kunstværk, som mange fysiske fænomener blev forklaret med, i fuld debat..
Boltzmann var en dygtig forsvarer af atomets eksistens og stod i sin tid for hård kritik af sit arbejde fra mange kolleger, der mente, at det indeholdt uopløselige paradokser..
Han erklærede, at observerbare fænomener på makroskopiske niveauer kunne forklares med de statistiske egenskaber for bestanddele, som f.eks. Atomer og molekyler..
Måske skyldtes denne kritik den dybe depression, der førte ham til at tage sit liv i begyndelsen af september 1906, da han stadig havde meget at gøre, da han blev betragtet som en af de store teoretiske fysikere i sin tid, og der var meget lidt tilbage at andre forskere bidrager til at bekræfte sandheden i deres teorier.
Det varede ikke længe efter hans død, at nye opdagelser om atomets natur og dets bestanddele kom sammen for at bevise Boltzmann ret..
Nu, Boltzmann-konstanten kB det blev introduceret som det er kendt i dag et stykke tid efter værkerne fra den østrigske fysiker. Det var Max Planck, i hans lov om udsendelse af den sorte krop, et værk, som han præsenterede i 1901, der på det tidspunkt gav det værdien 1,34 x 10−23 J / K.
Omkring 1933 blev en plak med definitionen af entropi, der involverer den berømte konstant, føjet til Boltzmanns gravsten i Wien som en postume hyldest: S = kB log W, ligning, som vil blive diskuteret senere.
I dag er Boltzmann-konstanten uundværlig i anvendelsen af termodynamikens love, statistiske mekanik og informationsteori, hvor denne triste fysiker var en pioner..
Gasser kan beskrives i makroskopiske termer og også i mikroskopiske termer. Til den første beskrivelse er der begreber som tæthed, temperatur og tryk.
Det skal dog huskes, at en gas er sammensat af mange partikler, som har en global tendens til en bestemt opførsel. Det er denne tendens, der måles makroskopisk. En måde at bestemme Boltzmann-konstanten på er takket være den velkendte idealgasligning:
p.V = n. R. T
Her s er gastrykket, V er dens volumen, n er antallet af tilstedeværende mol, R er gaskonstant og T er temperaturen. I en mol ideel gas er følgende forhold opfyldt mellem produktet p.V, og den translationelle kinetiske energi K hele sættet er:
p.V = (2/3). K
Derfor er den kinetiske energi:
K = (3/2) n.R.T
Ved at dividere med det samlede antal tilstedeværende molekyler, som kaldes N, opnås den gennemsnitlige kinetiske energi for en enkelt partikel:
OGc = K / N
OGc= (3 / 2N) n.R.T
I en mol er der Avogadros antal partikler NTIL, og derfor er det samlede antal partikler N = nNA, resterende:
OGc = (3 / 2nNTIL) n.R.T
Præcis kvotienten R / NTIL er Boltzmanns konstant, således at det vises, at den gennemsnitlige translationelle kinetiske energi af en partikel kun afhænger af den absolutte temperatur T og ikke af andre størrelser såsom tryk, volumen eller endda typen af molekyle:
OGc = (3/2) kB. T
En gas har en given temperatur, men den temperatur kan svare til forskellige tilstande af intern energi. Sådan visualiseres denne forskel?
Overvej det samtidige kast af 4 mønter og måderne, hvorpå de kan falde:
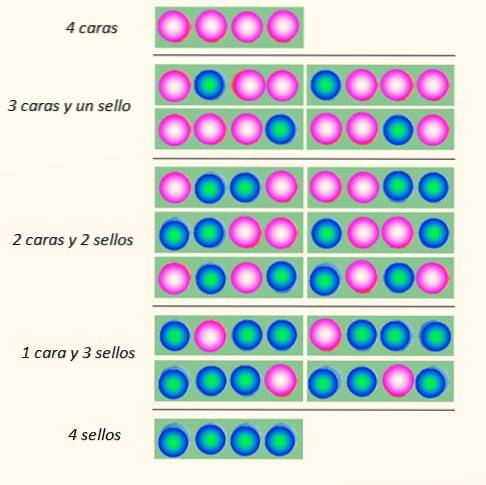
Møntsættet kan antage i alt 5 stater, der betragtes makroskopisk, beskrevet i figuren. Hvilke af disse stater vil læseren sige er den mest sandsynlige?
Svaret skal være tilstanden på 2 hoveder og 2 haler, fordi du har i alt 6 muligheder, af de 16 illustreret i figuren. Og 24 = 16. Disse svarer til staterne mikroskopisk.
Hvad hvis der kastes 20 mønter i stedet for 4? Der ville være i alt 2tyve muligheder eller "mikroskopiske tilstande". Det er et meget større antal og sværere at håndtere. For at lette håndteringen af et stort antal er logaritmer meget passende.
Nu, hvad der synes åbenlyst er, at den stat med den mest uorden er den mest sandsynlige. Mere bestilte stater som 4 hoveder eller 4 segl er lidt mindre sandsynlige.
Entropien af en makroskopisk tilstand S defineres som:
S = kB ln w
Hvor w er antallet af mulige mikroskopiske tilstande i systemet og kB er Boltzmanns konstant. Hvad ln w er dimensionsløs, entropi har de samme enheder som kB: Joule / K.
Dette er den berømte ligning på Boltzmanns gravsten i Wien. Men mere end entropi, hvad der er relevant er dens ændring:
AS = kB ln wto - kB ln w1 = kB ln (wto/ w1)
Værdien af Boltzmanns konstant opnås eksperimentelt med ekstrem præcision med målinger baseret på akustisk termometri, som udføres ved hjælp af den egenskab, der fastslår afhængigheden af lydhastigheden i en gas med dens temperatur.
Faktisk er lydhastigheden i en gas givet ved:
Badiabatisk = γp
Og ρ er densiteten af gassen. For ovenstående ligning, s er det pågældende gasstryk og γ er den adiabatiske koefficient, hvis værdi for en given gas findes i tabeller.
Metrologiinstitutter eksperimenterer også med andre måder at måle konstanten på, f.eks Johnson støjtermometri, der bruger termiske udsving, der forekommer tilfældigt i materialer, især ledere.
Finde:
a) Gennemsnitlig translationel kinetisk energi OGc som har et ideelt gasmolekyle ved 25 ºC
b) translationel kinetisk energi K af molekylerne i 1 mol af denne gas
c) Den gennemsnitlige hastighed for et iltmolekyle ved 25 ºC
milt = 16 x 10 -3 kg / mol
til) OGc = (3/2) k T = 1,5 x 1.380649 x 10-2. 3J. K-1 x 298 K = 6,2 x 10-enogtyve J
b) K = (3/2) n.R.T = 5 x 1 mol x 8,314 J / mol. K x 298 K = 3716 J
c) OGc = ½ mvto, under hensyntagen til, at iltmolekylet er diatomisk, og den molære masse skal ganges med 2, vil vi have:
Find ændringen i entropi, når 1 mol gas optager et volumen på 0,5 m3 udvides til at optage 1 m3.
AS = kB ln (wto/ w1)
wto= 2Nw1 (Der var 24 mikroskopiske tilstande til kastet af de 4 mønter, kan du huske?)
Hvor N er antallet af partikler til stede i 0,5 mol gas 0,5 x NTIL:
AS = kB ln (2N w1/ w1) = kB i 2N= kB 0,5NTIL ln 2 = 2,88 J / K
Endnu ingen kommentarer