
Eksempler på rektangulære koordinater og løste øvelser
Det rektangulære koordinater eller kartesisk er dem, der opnås ved ortogonisk at projicere på de tre kartesiske akser X, Y, Z et punkt placeret i et tredimensionelt rum.
Kartesiske akser er indbyrdes orienterede linjer vinkelret på hinanden. I det kartesiske koordinatsystem tildeles hvert punkt i rummet tre reelle tal, som er dets rektangulære koordinater.
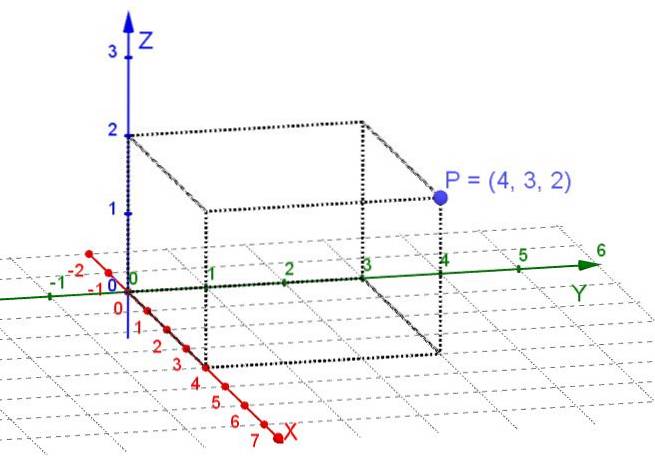
Et plan er et underrum af tredimensionelt rum. I tilfælde af at overveje punkter på et plan er det nok at vælge et par vinkelrette akser X, Y som det kartesiske system. Derefter tildeles hvert punkt på planet to reelle tal, der er dets rektangulære koordinater.
Artikelindeks
- 1 Oprindelse af rektangulære koordinater
- 2 Det kartesiske plan
- 2.1 Afstand mellem to punkter
- 2.2 Analytisk udtryk for en linje
- 3 eksempler
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Oprindelse af rektangulære koordinater
Rektangulære koordinater blev oprindeligt foreslået af den franske matematiker René Descartes (1596 og 1650), hvorfor de kaldes kartesisk.
Med denne idé fra Descartes tildeles punkterne på planet og rummet tal, så de geometriske figurer har en algebraisk ligning, og de klassiske geometriske sætninger kan bevises algebraisk. Med kartesiske koordinater fødes analytisk geometri.
Det kartesiske fly
Hvis der i et plan vælges to vinkelrette linjer, der krydser hinanden ved et punkt O; og hvis hver linje derudover tildeles en retning og en numerisk skala mellem efter hinanden ligeværdige punkter, så er der et kartesisk system eller plan, hvor hvert punkt i planet er forbundet med et ordnet par af to reelle tal, der er deres fremskrivninger henholdsvis på X- og Y-akserne.
Punktene A = (3, 2); B = (- 2, 3); C = (- 2, -3) og D = (3, -3) er repræsenteret i det kartesiske plan som vist nedenfor:
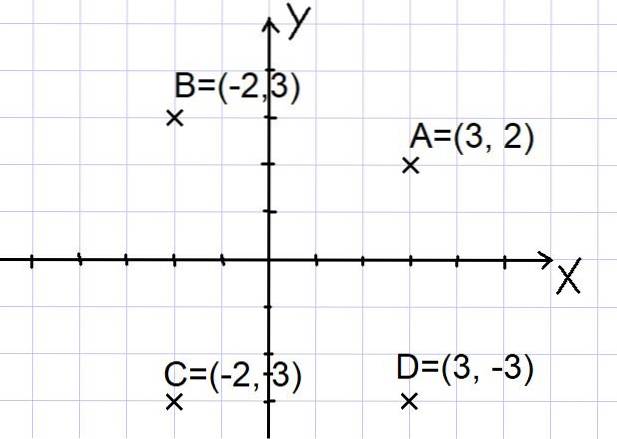
Bemærk, at de to akser X og Y deler planet i fire sektorer kaldet kvadranter. Punkt A er i den første kvadrant, B er i den anden kvadrant, C er i den tredje kvadrant, og punkt D er i den fjerde kvadrant..
Afstand mellem to punkter
Afstanden mellem to punkter A og B på det kartesiske plan er længden af det segment, der forbinder dem. Denne afstand kan beregnes analytisk som følger:
d (A, B) = √ (Bx - Ax) ^ 2 + (By - Ay) ^ 2)
Ovenstående formel opnås ved anvendelse af Pythagoras sætning.
Anvendelse af denne formel til punkt A, B i figur 2 har vi:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Det vil sige d (A, B) = 5,10 enheder. Bemærk, at afstanden blev opnået uden behov for at måle med en lineal, en fuldstændig algebraisk procedure er blevet fulgt.
Analytisk udtryk for en linje
Rektangulære koordinater tillader den analytiske repræsentation af grundlæggende geometriske objekter såsom punktet og linjen. To punkter A og B definerer en enkelt linje. Linjens hældning defineres som kvotienten mellem forskellen mellem Y-koordinaterne for punkt B minus A divideret med forskellen mellem X-koordinaterne for punkt B minus A:
hældning = (By - Ay) / (Bx - Ax)
Ethvert punkt P af koordinater (x, y), der hører til linjen (AB), skal have samme hældning:
hældning = (y - Ay) / (x - Ax)
Ligningen, der opnås ved hjælp af løjperne, er den analytiske eller algebraiske repræsentation af linjen, der passerer gennem punkterne A og B:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Hvis vi tager de rektangulære koordinater i figur 2 for A og B, har vi:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
I dette særlige tilfælde har vi en linje med en negativ hældning -⅕, hvilket betyder at ved at placere på et punkt på linjen og øge x-koordinaten med en enhed, falder y-koordinaten med 0,2 enheder.
Den mest almindelige måde at skrive ligningen på linjen i planet er med y-koordinaten ryddet som en funktion af variablen x:
y = - (1/5) x + 13/5
Eksempler
Eksempel 1
Opnå ved analytiske metoder afstanden mellem punkterne C og A, idet de er de rektangulære koordinater for C = (-2, -3) og dem for A = (3,2).
Formlen for den euklidiske afstand mellem disse to punkter er skrevet således:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Ved at erstatte deres tilsvarende rektangulære koordinater har vi:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Eksempel 2
Få ligningen af den linje, der passerer gennem punktet C for koordinaterne (-2, -3) og punktet P for koordinaterne (2, 0).
For det første opnås hældningen af linjen CP:
hældning = (0 - (- 3)) / (2 - (-2)) = ¾
Ethvert punkt Q for generiske rektangulære koordinater (x, y), der hører til linjen CP, skal have samme hældning:
hældning = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
Ligningen med linjen CP er med andre ord:
(y +3) / (x +2) = ¾
En alternativ måde at skrive ligningen på linjen CP er at løse for y:
y = ¾ x - 3/2
Løst øvelser
Øvelse 1
Få de rektangulære koordinater for skæringspunktet mellem linjerne y = - (1/5) x + 13/5 og linjen y = ¾ x - 3/2.
Løsning: Skæringspunktet for de to linjer deler pr. Definition de samme rektangulære koordinater. Derfor er y-koordinaterne ved skæringspunktet identiske for begge linjer:
-(1/5) x + 13/5 = ¾ x - 3/2
hvilket fører til følgende udtryk:
(¾ + ⅕) x = 13/5 +3/2
løse summen af brøk, vi får:
19/20 x = 41/10
Løsning for x:
x = 82/19 = 4,32
For at opnå y-skæringspunktet erstattes den opnåede x-værdi i en af linjerne:
y = ¾ 4,32 - 3/2 = 1,74
Dette betyder, at de givne linjer krydser hinanden ved punktet I af koordinaterne I = (4,32, 1,74).
Øvelse 2
Få ligningen af omkredsen, der passerer gennem punktet R for de rektangulære koordinater (3, 4), og som har centrum ved koordinaternes oprindelse.
Løsning: Radius R er afstanden fra punkt R til oprindelsen O for koordinater (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Det vil sige, det er en cirkel med radius 5 centreret ved (0,0).
Ethvert punkt P (x, y) på omkredsen skal have samme afstand 5 fra centrum (0, 0), så det kan skrives:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
Nemlig:
√ (x ^ 2 + y ^ 2) = 5
For at fjerne kvadratroden er begge medlemmer af ligestillingen kvadreret og opnår:
x ^ 2 + y ^ 2 = 25
Hvad er ligningen af omkredsen.
Dette eksempel illustrerer kraften i det rektangulære koordinatsystem, som gør det muligt at bestemme geometriske objekter, såsom omkredsen, uden behov for at bruge papir, blyant og kompas. Den ønskede omkreds er udelukkende bestemt ved algebraiske metoder.
Referencer
- Arfken G og Weber H. (2012). Matematiske metoder til fysikere. En omfattende guide. 7. udgave. Akademisk presse. ISBN 978-0-12-384654-9
- Beregning cc. Løste problemer med rektangulære koordinater. Gendannet fra: calculo.cc
- Weisstein, Eric W. "Kartesiske koordinater." Fra MathWorld-A Wolfram Web. Gendannet fra: mathworld.wolfram.com
- wikipedia. Kartesisk koordinatsystem. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer