
Triangle ulighed demonstration, eksempler, løste øvelser
Det kaldes ulighed i trekanten til egenskaben af to reelle tal, der består i, at den absolutte værdi af deres sum altid er mindre end eller lig med summen af deres absolutte værdier. Denne egenskab er også kendt som Minkowski ulighed eller trekantet ulighed.
Denne egenskab af tal kaldes trekantet ulighed, fordi det i trekanter sker, at længden af den ene side altid er mindre end eller lig med summen af de to andre, selvom denne ulighed ikke altid gælder i området med trekanter..

Der er flere beviser for den trekantede ulighed i reelle tal, men i dette tilfælde vælger vi en baseret på egenskaberne for den absolutte værdi og det binomiale kvadrat.
Sætning: For hvert par tal til Y b vedrørende de reelle tal skal den:
| a + b | ≤ | til | + | b |
Artikelindeks
- 1 demo
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 2.4 Eksempel 4
- 2.5 Eksempel 5
- 2.6 Eksempel 6
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 4
- 4 Referencer
Demonstration
Vi begynder med at overveje det første medlem af uligheden, som vil være kvadratisk:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (ligning 1)
I det foregående trin brugte vi egenskaben, at et hvilket som helst tal i kvadrat er lig med den absolutte værdi af det nævnte tal i kvadrat, det vil sige: | x | ^ 2 = x ^ 2. Udviklingen af den firkantede binomial er også blevet brugt.
Alt nummer x er mindre end eller lig med dets absolutte værdi. Hvis tallet er positivt, er det lige, men hvis tallet er negativt, vil det altid være mindre end et positivt tal. I dette tilfælde sin egen absolutte værdi, det vil sige, at det kan siges at x ≤ | x |.
Produktet (a b) er et tal, derfor gælder det, at (a b) ≤ | a b |. Når denne egenskab anvendes på (ligning 1) har vi:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (ligning 2)
Under hensyntagen til det | a b | = | a || b | (Ligning 2) kan skrives som følger:
| a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (ligning 3)
Men da vi tidligere sagde, at firkantet af et tal er lig med den absolutte værdi af antallet i kvadrat, så kan ligning 3 omskrives som følger:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (ligning 4)
I det andet medlem af uligheden anerkendes et bemærkelsesværdigt produkt, som når det anvendes fører til:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (ligning 5)
I det forrige udtryk skal det bemærkes, at de værdier, der skal kvadreres i begge medlemmer af uligheden, er positive, derfor skal det også være tilfreds med, at:
| a + b | ≤ (| a | + | b |) (Ligning 6)
Ovenstående udtryk er nøjagtigt hvad man ønskede at demonstrere.
Eksempler
Dernæst vil vi kontrollere den trekantede ulighed med flere eksempler.
Eksempel 1
Vi tager værdien a = 2 og værdien b = 5, det vil sige begge positive tal, og vi kontrollerer, om uligheden er opfyldt eller ej.
| 2 + 5 | ≤ | 2 | + | 5 |
| 7 | ≤ | 2 | + | 5 |
7 ≤ 2+ 5
Ligestilling er verificeret, derfor er trekantens ulighedssætning blevet opfyldt.
Eksempel 2
Følgende værdier er valgt a = 2 og b = -5, det vil sige et positivt tal og det andet negative, vi kontrollerer, om uligheden er opfyldt eller ej.
| 2 - 5 | ≤ | 2 | + | -5 |
| -3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
Uligheden er opfyldt, derfor er den trekantede ulighedssætning blevet bekræftet.
Eksempel 3
Vi tager værdien a = -2 og værdien b = 5, det vil sige et negativt tal og den anden positive, vi kontrollerer, om uligheden er opfyldt eller ej.
| -2 + 5 | ≤ | -2 | + | 5 |
| 3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
Uligheden er bekræftet, derfor er sætningen opfyldt.
Eksempel 4
Følgende værdier er valgt a = -2 og b = -5, det vil sige begge negative tal, og vi kontrollerer, om uligheden er opfyldt eller ej.
| -2 - 5 | ≤ | -2 | + | -5 |
| -7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
Lighed er verificeret, derfor er Minkowskis ulighedssætning blevet opfyldt.
Eksempel 5
Vi tager værdien a = 0 og værdien b = 5, det vil sige et tal nul og den anden positive, så kontrollerer vi, om uligheden er opfyldt eller ej.
| 0 + 5 | ≤ | 0 | + | 5 |
| 5 | ≤ | 0 | + | 5 |
5 ≤ 0+ 5
Lighed er opfyldt, derfor er trekant-ulighedssætningen blevet bekræftet.
Eksempel 6
Vi tager værdien a = 0 og værdien b = -7, det vil sige et tal nul og den anden positive, så kontrollerer vi, om uligheden er opfyldt eller ej.
| 0 - 7 | ≤ | 0 | + | -7 |
| -7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
Lighed er verificeret, derfor er den trekantede ulighedssætning opfyldt.
Løst øvelser
I de følgende øvelser repræsenterer geometrisk trekantsulighed eller Minkowski-ulighed for tallene a og b.
Tallet a vil blive repræsenteret som et segment på X-aksen, dets oprindelse O falder sammen med nul på X-aksen, og den anden ende af segmentet (ved punkt P) vil være i den positive retning (til højre) for X-akse hvis a> 0, men hvis a < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
Tilsvarende vil tallet b blive repræsenteret som et segment, hvis oprindelse er på punkt P. Den anden ekstreme, det vil sige punkt Q vil være til højre for P, hvis b er positiv (b> 0) og punkt Q vil være | b | enheder til venstre for P, hvis b<0.
Øvelse 1
Graf trekantens ulighed for a = 5 og b = 3 | a + b | ≤ | til | + | b |, være c = a + b.
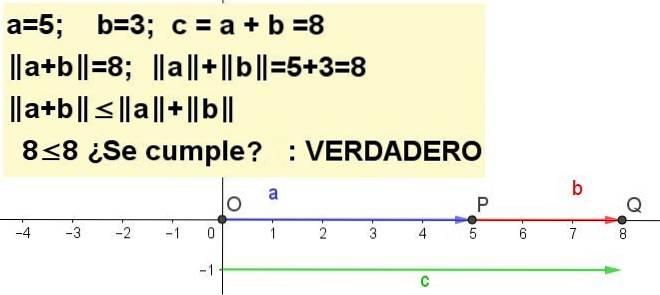
Øvelse 2
Graf den trekantede ulighed for a = 5 og b = -3.
| a + b | ≤ | til | + | b |, være c = a + b.

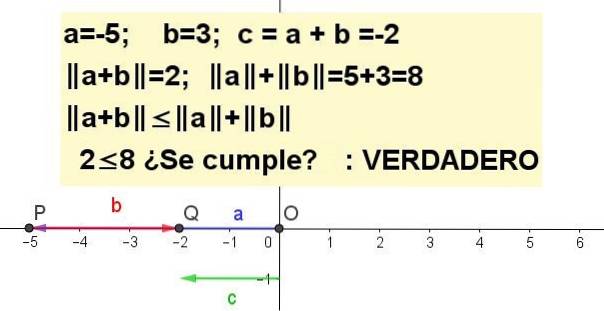
Øvelse 3
Vis trekantens ulighed grafisk for a = -5 og b = 3.
| a + b | ≤ | til | + | b |, være c = a + b.
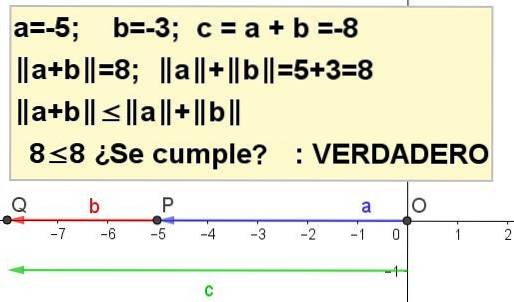
Øvelse 4
Konstruer grafisk den trekantede ulighed for a = -5 og b = -3.
| a + b | ≤ | til | + | b |, være c = a + b.
Referencer
- E. Whitesitt. (1980). Boolsk algebra og dens anvendelser. Redaktionelt selskab Continental C. A.
- Mícheál O 'Searcoid. (2003) Elementer af abstrakt analyse ... Institut for matematik. University College Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Matematik og teknik inden for datalogi. Institut for Computervidenskab og Teknologi. National Bureau of Standards. Washington, D.C. 20234
- Eric Lehman. Matematik til datalogi. Google Inc..
- F Thomson Leighton (1980). Calculus. Institut for Matematik og Computer Science and AI Laboratory, Massachusetts Institute of Technology.
- Khan Academy. Triangle Inequality Theorem. Gendannet fra: khanacademy.org
- Wikipedia. Trekantet ulighed. Gendannet fra: es. wikipedia.com



Endnu ingen kommentarer