Formel for første grads ligninger, hvordan man løser dem, f.eks. Øvelser

Det første grad eller lineære ligninger med et ukendt er dem, der kan udtrykkes som summen af ​​to udtryk som følger:

ax + b = 0

Hvor a og b, med til ≠ 0, er reelle tal R eller også komplekse C. For at løse det transponeres termer, hvilket betyder at ændre vilkår fra den ene side af ligestillingen til den anden.

For at løse det ukendte er udtrykket + b transponeret, hvilket skal gå til højre side af ligestillingen med ændret tegn.

økse = -b

Derefter ryddes værdien af ​​x således:

x = - b / a

Som et eksempel skal vi løse følgende ligning:

6x - 5 = 4

Vi transponerer -5-udtrykket til højre med et ændret tegn:

6x = 4 + 5

Dette svarer til at tilføje 5 til begge sider af den oprindelige ligning:

6x - 5 + 5 = 4 + 5 → 6x = 9

Og nu løser vi det ukendte "x":

x = 9/6 = 3/2

Hvilket svarer til at dividere begge sider af ligestillingen med 6. Så vi kan bruge følgende til at få løsningen:

-Den samme mængde kan tilføjes eller trækkes fra begge sider af ligestillingen i en ligning uden at ændre den.

-Du kan også multiplicere (eller dele) med det samme beløb alle termerne både til venstre og til højre for ligningen.

-Og hvis begge medlemmer af en ligning hæves til samme magt, ændres ligestillingen heller ikke.

Artikelindeks

• 1 Sådan løses første grads ligninger
  • 1.1 Grafisk fortolkning
• 2 Eksempler på enkle lineære ligninger   
  • 2.1 Heltalsligninger
  • 2.2 Brøkligninger
  • 2.3 Bogstavelige ligninger
  • 2.4 Systemer af første grad ligninger 
  • 2.5 Lineære ligninger med absolut værdi
• 3 enkle løste øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
  • 3.3 - Øvelse 3
• 4 Referencer

Sådan løses første grads ligninger

Løsningen af ​​en ligning af første grad er også kendt som dens rod. Det er værdien af ​​x, der omdanner det originale udtryk til en lighed. For eksempel i:

5x = 8x - 15

Hvis vi erstatter x = 5 i denne ligning, får vi:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Da lineære ligninger af første grad kommer i mange former, som nogle gange ikke er indlysende, er der en række generelle regler, der inkluderer forskellige algebraiske manipulationer for at finde værdien af ​​det ukendte:

-Først og fremmest, hvis der er angivet operationer, skal de udføres.

-Gruppering af symboler som parenteser, firkantede parenteser og parenteser, hvis nogen, bør fjernes, så de relevante tegn holdes.

-Vilkårene er transponeret for at placere alle dem, der indeholder det ukendte på den ene side af ligestillingen, og dem, der ikke indeholder det på den anden.

-Derefter reduceres alle lignende vilkår for at nå frem til formularen økse = -b.

-Og det sidste trin er at rydde det ukendte.

Grafisk fortolkning

Den første grads ligning hævet i starten kan afledes af ligningen af ​​linjen y = mx + c, hvilket gør y = 0. Den resulterende værdi af x svarer til skæringspunktet mellem linjen og den vandrette akse.

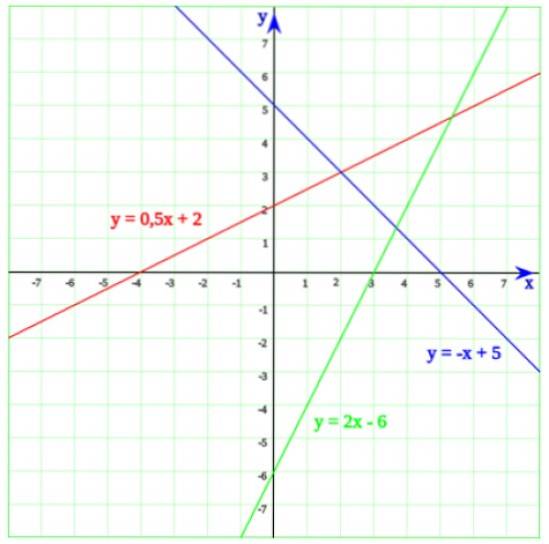
I den følgende figur er der tre linjer. Startende med den grønne linje, hvis ligning er:

y = 2x - 6

Ved at gøre y = 0 i ligningen af ​​linjen opnås den første grads ligning:

2x - 6 = 0

Hvis løsning er x = 6/2 = 3. Nu når vi detaljerer grafen, er det let at indse, at linjen i virkeligheden skærer den vandrette akse ved x = 3.

Den blå linje skærer x-aksen ved x = 5, hvilket er løsningen på ligningen -x + 5 = 0. Endelig skærer linjen, hvis ligning er y = 0,5x + 2, x-aksen ved x = - 4 , som let kan ses fra ligningen af ​​den første grad:

0,5 x + 2 = 0

x = 2 / 0,5 = 4

Eksempler på enkle lineære ligninger   

Heltalsligninger

Det er dem, hvis udtryk der ikke er nævnere, for eksempel:

21 - 6x = 27 - 8x

Din løsning er:

-6x + 8x = 27 - 21

2x = 6

x = 3

Brøklige ligninger

Disse ligninger indeholder mindst en anden nævner end 1. For at løse dem er det tilrådeligt at multiplicere alle termerne med det mindst almindelige multiple (LCM) af nævnere for at eliminere dem.

Følgende ligning er fraktioneret type:

Da disse tal er små, er det ikke svært at se, at m.c.m (6, 8,12) = 24. Dette resultat opnås let ved at udtrykke tallene som et produkt af primtal eller deres kræfter, lad os se:

6 = 3,2

8 = 2³

12 = 2^to⋅3

Det mindst almindelige multipel bestemmes ved at multiplicere de fælles og usædvanlige faktorer 6, 8 og 12 med deres største eksponent, derefter:

lcm (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Da vi har det mindst fælles multiplum, skal det ganges med hver af ligningerne:

4 (x + 5) -3 (2x + 3) = 2 (1-5x)

Vi gør brug af den distribuerende ejendom:

4x + 20 - 6x -9 = 2 - 10x

Alle termer, der indeholder det ukendte "x", er grupperet på venstre side af ligestillingen, hvilket efterlader de uafhængige eller numeriske udtryk på højre side:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Bogstavelige ligninger

De er lineære ligninger med en ukendt, som dog ledsages af bogstavelige koefficienter (bogstaver). Disse bogstaver behandles på samme måde som tal. Et eksempel på en bogstavelig første gradsligning er:

-3ax + 2a = 5x - b

Denne ligning løses på samme måde som om de uafhængige udtryk og koefficienter var numeriske:

-3ax - 5x = - b - 2a

Faktorering af det ukendte "x":

x (-3a - 5) = - b - 2a

x = (- b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Systemer af ligninger af første grad 

Ligningssystemer består af et sæt ligninger med to eller flere ukendte. Systemets løsning består af værdier, der tilfredsstiller ligningerne samtidigt og for at bestemme det utvetydigt, skal der være en ligning for hver ukendt.

Den generelle form for et system af m lineære ligninger med n ukendte er:

til_ellevex₁ + til₁₂x_to +… til_1nx_n = b₁
til_enogtyvex₁ + til₂₂x_to +… til_2nx_n = b_to
...
til_m1x₁ + til_m2x_to +… til_mnx_n = b_m

Hvis systemet har en løsning, siges det at være det kompatibel bestemt, når der er et uendeligt sæt værdier, der tilfredsstiller det, er det ubestemt kompatibel, og endelig hvis det ikke har nogen løsning, så er det uforenelig.

Til løsning af systemer med lineære ligninger anvendes flere metoder: reduktion, substitution, udligning, grafiske metoder, Gauss-Jordan eliminering og brugen af ​​determinanter er blandt de mest anvendte. Men der er andre algoritmer, der kan nå løsningen, mere bekvemt for systemer med mange ligninger og ukendte.

Et eksempel på et system med lineære ligninger med to ukendte er:

8x - 5 = 7y - 9
6x = 3y + 6

Løsningen på dette system præsenteres senere i afsnittet om løste øvelser..

Lineære ligninger med absolut værdi

Den absolutte værdi af et reelt tal er afstanden mellem dets placering på nummerlinjen og 0 på nummerlinjen. Da det er en afstand, er dens værdi altid positiv.

Den absolutte værdi af et tal betegnes med modulostængerne: │x│. Den absolutte værdi af et positivt eller negativt tal er altid positiv, for eksempel:

│ + 8│ = 8

│-3│ = 3

I en absolut ligning er det ukendte mellem modulstænger. Lad os overveje følgende enkle ligning:

│x│ = 10

Der er to muligheder, den første er, at x er et positivt tal, i hvilket tilfælde vi har:

x = 10

Og den anden mulighed er, at x er et negativt tal, i dette tilfælde:

x = -10

Dette er løsningerne i denne ligning. Lad os nu se på et andet eksempel:

│x + 6│ = 11

Mængden inde i bjælkerne kan være positiv, så:

x + 6 = 11

x = 11 -6 = 5

Eller det kan være negativt. I det tilfælde:

-(x + 6) = 11

-x - 6 = 11 ⇒ -x = 11 + 6 = 17

Og værdien af ​​det ukendte er:

x = -17

Denne absolutte ligning har derfor to løsninger: x₁ = 5 og x_to = -17. Vi kan kontrollere, at begge løsninger fører til en lighed i den oprindelige ligning:

│5 + 6│ = 11

│11│ = 11

Y

│-17 + 6│ = 11

│-11│ = 11

Enkle løste øvelser

- Øvelse 1

Løs følgende system med lineære ligninger med to ukendte:

8x - 5 = 7y -9
6x = 3y + 6

Opløsning

Som det foreslås, er dette system ideelt til at bruge substitutionsmetoden, da i den anden ligning det ukendte x er næsten klar til klarering:

x = (3y + 6) / 6

Og det kan straks erstattes i den første ligning, som derefter bliver en første grads ligning med ukendt "y":

8 [(3y + 6) / 6] - 5 = 7y - 9

Nævneren kan fjernes ved at gange hvert udtryk med 6:

6. 8⋅ [(3y + 6) / 6] - 6,5 = 6,77-6. 9

8⋅ (3y + 6) - 30 = 42y - 54

Anvendelse af den distribuerende ejendom i første periode på retten til lighed:

24 år + 48-30 = 42 år - 54 ⇒ 24 år + 18 = 42 år - 54

Ligningen kan forenkles, da alle koefficienter er multipla af 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Med dette resultat går vi til clearing af x:

x = (3y +6) / 6 → x = (12 + 6) / 6 = 3

- Øvelse 2

Løs følgende ligning:

Opløsning

Produkter vises i denne ligning, og efter instruktionerne i starten skal de først udvikles:

3x - 10x +14 = 5x + 36x + 12

Derefter føres alle termer, der indeholder de ukendte, til venstre side af ligestillingen, og til højre er de uafhængige udtryk:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Øvelse 3

Tilføjelse af de tre indvendige vinkler i en trekant giver 180º. Major overskrider mindreårige med 35 °, og sidstnævnte overstiger igen med 20 ° forskellen mellem dur og medium. Hvad er vinklerne??

Opløsning

Vi kalder “x” den større vinkel, “y” den midterste og “z” den mindste. Når erklæringen bekræfter, at summen af ​​dem er 180º, kan den skrives:

x + y + z = 180

Så ved vi, at jo større overstiger mindre med 35º, kan vi skrive dette sådan:

x = z + 35

Endelig overstiger den mindste forskellen mellem den største og den midterste med 20º:

z = x - y + 20

Vi har et system med 3 ligninger og 3 ukendte:

x + y + z = 180

x = z + 35

z = x - y + 20

Løsning for z fra den første ligning, vi har:

z = 180 - x - y

Matcher med det tredje:

180 - x - y = x - y + 20

At sende de ukendte til venstre som altid:

-x - y - x + y = 20 - 180

"Y" annulleres og forbliver:

-2x = - 160

x = 80º

Fra den anden ligning finder vi værdien af ​​z:

z = x - 35 = 80 - 35 = 45º

Og værdien af ​​y findes fra første eller tredje:

y = 180 - x - z = 180 - 80 - 45 = 55º

Referencer

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturudgaver.
2. Monterey Institute. Ligninger, uligheder og absolut værdi. Gendannet fra: montereyinstitute.org.
3. Online lærer. Klassificering af lineære eller første grads ligninger. Gendannet fra: profesorenlinea.cl.
4. Hoffman, J. Selection of Mathematics Topics. Bind 2.
5. Jiménez, R. 2008. Algebra. Prentice hall.
6. Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.