Det polynomiske ligninger De er en erklæring, der hæver ligestillingen mellem to udtryk eller medlemmer, hvor mindst et af udtrykkene, der udgør hver side af ligestillingen, er polynomer P (x). Disse ligninger er navngivet efter graden af deres variabler.
Generelt er en ligning en erklæring, der etablerer ligestillingen mellem to udtryk, hvor der i mindst en af disse er ukendte størrelser, der kaldes variabler eller ukendte. Selv om der er mange typer ligninger, klassificeres de generelt i to typer: algebraisk og transcendental..
Polynomiske ligninger indeholder kun algebraiske udtryk, som kan have en eller flere ukendte involveret i ligningen. Ifølge den eksponent (grad) de har, kan de klassificeres i: første grad (lineær), anden grad (kvadratisk), tredje grad (kubisk), fjerde grad (kvartisk), grad større end eller lig med fem og irrationel.
Artikelindeks
Polynomlige ligninger er udtryk, der er dannet af en lighed mellem to polynomer; det vil sige med de endelige summer af multiplikationer mellem ukendte værdier (variabler) og faste tal (koefficienter), hvor variablerne kan have eksponenter, og deres værdi kan være et positivt heltal inklusive nul.
Eksponenterne bestemmer graden eller typen af ligning. Udtrykket for det udtryk, der har den højeste værdi eksponent, repræsenterer den absolutte grad af polynomet.
Polynomligninger er også kendt som algebraisk, deres koefficienter kan være reelle eller komplekse tal, og variablerne er ukendte tal repræsenteret af et bogstav, såsom: "x".
Hvis en værdi erstattes af variablen "x" i P (x), er resultatet lig med nul (0), så siges denne værdi at tilfredsstille ligningen (det er en løsning) og kaldes generelt roden til polynomet.
Når du udvikler en polynomligning, vil du finde alle rødderne eller løsningerne.
Der er flere typer polynomiske ligninger, som er differentieret i henhold til antallet af variabler og også i henhold til graden af deres eksponent.
Polynomligningerne - hvor dens første sigt er et polynom, der har et enkelt ukendt, i betragtning af at dets grad kan være et hvilket som helst naturligt tal (n) og det andet sigt er nul - kan således udtrykkes som følger:
tiln * xn + tiln-1 * xn-1 +… + A1 * x1 + til0 * x0 = 0
Hvor:
- tiln, tiln-1 allerede0, er reelle koefficienter (tal).
- tiln er forskellig fra nul.
- Eksponenten n er et positivt heltal, der repræsenterer ligningsgraden.
- x er den variabel eller ukendt, der skal søges.
Den absolutte eller større grad af en polynomligning er eksponenten med den højeste værdi blandt alle dem, der danner polynomet; ligningerne klassificeres således som:
Første grad polynomiske ligninger, også kendt som lineære ligninger, er dem, hvor graden (den største eksponent) er lig med 1, polynomet har formen P (x) = 0; og det er sammensat af et lineært udtryk og et uafhængigt. Den er skrevet som følger:
ax + b = 0.
Hvor:
- a og b er reelle tal og a ≠ 0.
- økse er det lineære udtryk.
- b er det uafhængige udtryk.
For eksempel er ligningen 13x - 18 = 4x.
For at løse lineære ligninger skal alle termer, der indeholder det ukendte x, videregives til den ene side af ligestillingen, og de, der ikke har, flytter de til den anden side for at løse det og opnå en løsning:
13x - 18 = 4x
13x = 4x + 18
13x - 4x = 18
9x = 18
x = 18 ÷ 9
x = 2.
Således har den givne ligning kun en løsning eller rod, som er x = 2.
Andegrads polynomiske ligninger, også kendt som kvadratiske ligninger, er dem, hvor graden (den største eksponent) er lig med 2, polynomet har formen P (x) = 0 og er sammensat af et kvadratisk udtryk, en lineær og en uafhængig. Det udtrykkes som følger:
økseto + bx + c = 0.
Hvor:
- a, b og c er reelle tal og a ≠ 0.
- økseto er det kvadratiske udtryk, og "a" er koefficienten for det kvadratiske udtryk.
- bx er det lineære udtryk, og "b" er koefficienten for det lineære udtryk.
- c er det uafhængige udtryk.
Generelt gives løsningen på denne type ligninger ved at løse x fra ligningen, og den er som følger, der kaldes resolvent:
Der, (bto - 4ac) kaldes ligningens diskriminant, og dette udtryk bestemmer antallet af løsninger, som ligningen kan have:
- Ja (bto - 4ac) = 0, ligningen vil have en enkelt løsning, der er dobbelt; det vil sige, at den vil have to lige store løsninger.
- Ja (bto - 4ac)> 0, vil ligningen have to forskellige reelle løsninger.
- Ja (bto - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).
For eksempel har vi ligningen 4xto + 10x - 6 = 0, for at løse det skal du først identificere termerne a, b og c og derefter erstatte det i formlen:
a = 4
b = 10
c = -6.
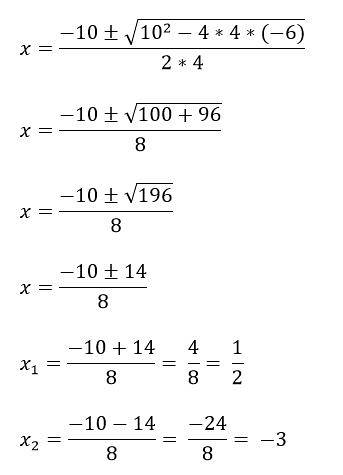
Der er tilfælde, hvor andengrads polynomiske ligninger ikke har alle tre termer, og det er derfor, de løses på en anden måde:
- I det tilfælde, at de kvadratiske ligninger ikke har det lineære udtryk (dvs. b = 0), vil ligningen udtrykkes som axto + c = 0. For at løse det skal du løse for xto og kvadratrødderne påføres hvert medlem, idet man husker at de to mulige tegn på, at det ukendte kan have, skal overvejes:
økseto + c = 0.
xto = - c ÷ a
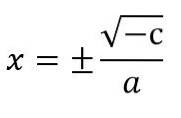
For eksempel 5 xto - 20 = 0.
5 xto = 20
xto = 20 ÷ 5
x = ± √4
x = ± 2
x1 = 2.
xto = -2.
- Når den kvadratiske ligning ikke har et uafhængigt udtryk (dvs. c = 0), udtrykkes ligningen som axto + bx = 0. For at løse det skal vi tage den fælles faktor for det ukendte x i det første medlem; Da ligningen er lig med nul, er det sandt, at mindst en af faktorerne vil være lig med 0:
økseto + bx = 0.
x (ax + b) = 0.
Således skal du:
x = 0.
x = -b ÷ a.
For eksempel: vi har ligningen 5xto + 30x = 0. Første faktor:
5xto + 30x = 0
x (5x + 30) = 0.
To faktorer genereres, som er x og (5x + 30). Det anses for, at en af disse vil være lig med nul, og den anden får en løsning:
x1 = 0.
5x + 30 = 0
5x = -30
x = -30 ÷ 5
xto = -6.
Polynomiske ligninger af højere grad er dem, der går fra tredje grad og fremefter, som kan udtrykkes eller løses med den generelle polynomligning for enhver grad:
tiln * xn + tiln-1 * xn-1 +… + A1 * x1 + til0 * x0 = 0
Dette bruges, fordi en ligning med en grad større end to er resultatet af faktorering af et polynom; det vil sige, det udtrykkes som multiplikation af polynomier af grad en eller større, men uden reelle rødder.
Løsningen af denne type ligninger er direkte, fordi multiplikationen af to faktorer vil være lig med nul, hvis nogen af faktorerne er nul (0); Derfor skal hver af de fundne polynomligninger løses, idet hver af dens faktorer er lig med nul.
For eksempel har vi tredje grad (kubisk) ligning x3 + xto +4x + 4 = 0. For at løse det skal følgende trin følges:
- Vilkårene er grupperet:
x3 + xto +4x + 4 = 0
(x3 + xto ) + (4x + 4) = 0.
- Medlemmerne nedbrydes for at få den fælles faktor for det ukendte:
xto (x + 1) + 4 (x + 1) = 0
(xto + 4)*(x + 1) = 0.
- På denne måde opnås to faktorer, som skal være lig med nul:
(xto + 4) = 0
(x + 1) = 0.
- Det kan ses, at faktoren (xto + 4) = 0 vil ikke have en reel løsning, mens faktoren (x + 1) = 0 vil have. Så løsningen er:
(x + 1) = 0
x = -1.
Løs følgende ligninger:
(2xto + 5)*(x - 3)*(1 + x) = 0.
I dette tilfælde udtrykkes ligningen som multiplikation af polynomer; det vil sige, det er indregnet. For at løse det skal hver faktor sættes til nul:
- 2xto + 5 = 0, har ingen løsning.
- x - 3 = 0
- x = 3.
- 1 + x = 0
- x = - 1.
Den givne ligning har således to løsninger: x = 3 og x = -1.
x4 - 36 = 0.
Der blev givet et polynom, som kan omskrives som en forskel i firkanter for at nå frem til en hurtigere løsning. Ligningen er således:
(xto + 6)*(xto - 6) = 0.
For at finde ligningen af ligningerne er begge faktorer sat til nul:
(xto + 6) = 0, har ingen løsning.
(xto - 6) = 0
xto = 6
x = ± √6.
Den oprindelige ligning har således to løsninger:
x = √6.
x = - √6.
Endnu ingen kommentarer