Det potentiel energi Det er den energi, som kroppe besidder i kraft af deres konfiguration. Når objekter interagerer, er der kræfter imellem dem, der er i stand til at udføre arbejde, og denne evne til at udføre arbejde, som er lagret i deres disposition, kan oversættes til energi..
For eksempel har mennesker udnyttet den potentielle energi fra vandfald siden umindelige tider, først ved spinding af møller og derefter ved vandkraftværker..
På den anden side har mange materialer en bemærkelsesværdig evne til at udføre arbejde ved at deformere og derefter vende tilbage til deres oprindelige størrelse. Og under andre omstændigheder tillader arrangementet af den elektriske ladning lagring af elektrisk potentiel energi, som for eksempel i en kondensator.
Potentiel energi giver mange muligheder for at blive omdannet til andre former for brugbar energi, deraf vigtigheden af at kende de love, der styrer den..
Artikelindeks
En genstands potentielle energi har sin oprindelse i de kræfter, der påvirker den. Imidlertid er potentiel energi en skalar størrelse, mens kræfter er vektor. Derfor er det tilstrækkeligt at angive dens numeriske værdi og de valgte enheder for at specificere den potentielle energi.
En anden vigtig kvalitet er den type kraft, som potentiel energi kan lagres med, da ikke alle kræfter har denne dyd. Kun konservative kræfter lagrer potentiel energi i de systemer, de virker på.
En konservativ kraft er en, for hvilken arbejdet ikke afhænger af stien, der følges af objektet, men kun af startpunktet og ankomstpunktet. Kraften, der driver det faldende vand, er tyngdekraften, som er en konservativ kraft.
På den anden side har elastiske og elektrostatiske kræfter også denne kvalitet, derfor er der potentiel energi forbundet med dem..
Styrker, der ikke opfylder ovennævnte krav kaldes ikke-konservative; eksempel på dem er i friktion og luftmodstand.
Da potentiel energi altid stammer fra konservative kræfter som dem, der allerede er nævnt, taler vi om tyngdepotentialenergi, elastisk potentiel energi, elektrostatisk potentiel energi, nuklear potentiel energi og kemisk potentiel energi..
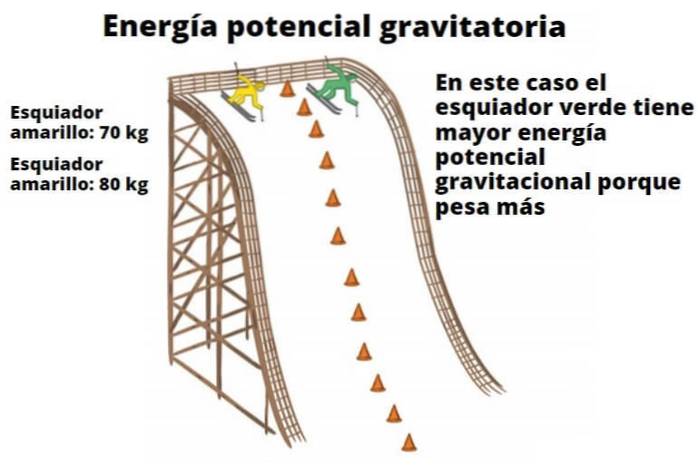
Ethvert objekt har potentiel energi som en funktion af dets højde fra jorden. Denne tilsyneladende enkle kendsgerning illustrerer, hvorfor faldende vand er i stand til at drive turbiner og til sidst omdannes til elektrisk energi. Skiløbereksemplet vist her viser også forholdet mellem vægt og højde til tyngdepotentialenergi.
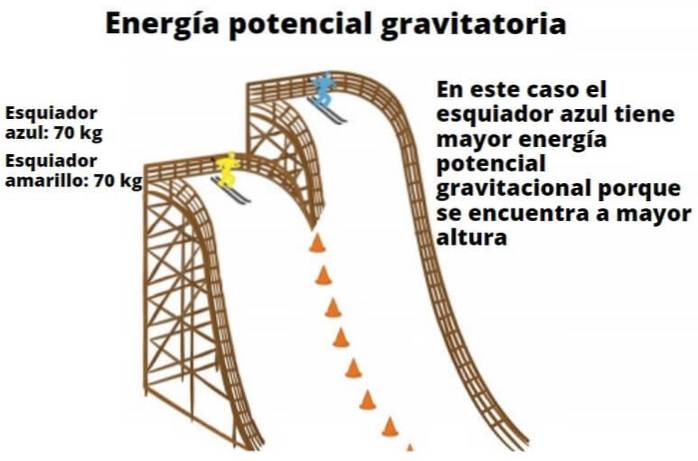
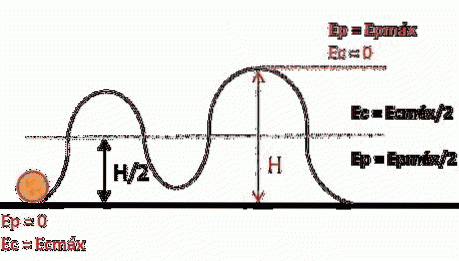
Et andet eksempel er en rutsjebane, som har højere potentiale energi, når den er i en bestemt højde over jorden. Når den har nået jordoverfladen, er dens højde lig med nul, og al dens potentielle energi er blevet omdannet til kinetisk energi (bevægelsesenergi).
Genstande som fjedre, buer, armbrøst og elastikker er i stand til at lagre elastisk potentiel energi..
Elastikken af et legeme eller et materiale er beskrevet af Hookes lov (op til visse grænser), som fortæller os, at den kraft, der er i stand til at udøve, når den komprimeres eller strækkes, er proportional med dens deformation.
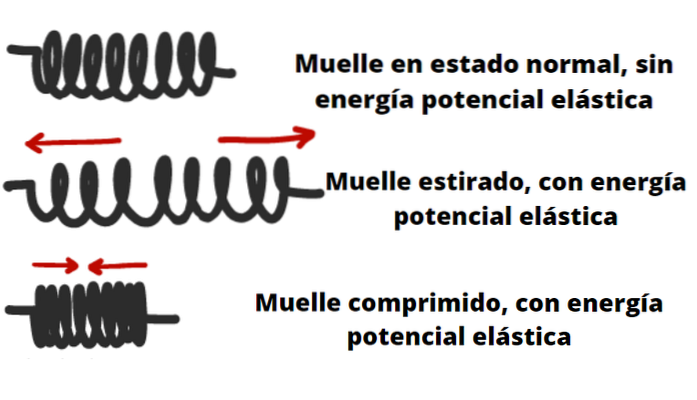
For eksempel i tilfælde af en fjeder eller fjeder betyder det, at jo mere den krymper eller strækker sig, jo større er den kraft, den kan udøve på en genstand placeret i den ene ende..
Det er energien, som elektriske ladninger har i kraft af deres konfiguration. Elektriske ladninger med det samme tegn frastøder hinanden, så for at placere et par positive - eller negative - ladninger i en bestemt position, skal en ekstern agent udføre arbejde. Ellers ville de have tendens til at adskille sig.
Dette arbejde opbevares på den måde, lasterne blev placeret. Jo tættere afgifterne på det samme tegn er, jo højere potentiel energi vil konfigurationen have. Det modsatte sker, når det kommer til masser af forskellige tegn; hvordan de tiltrækker, jo tættere de er, jo mindre potentiel energi har de.
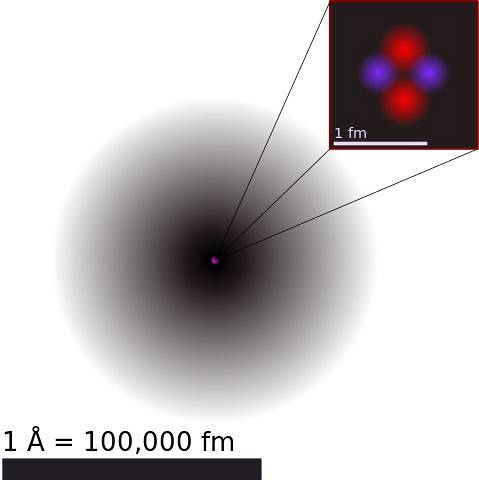
Atomkernen består af protoner og neutroner, generisk kaldet nukleoner. Førstnævnte har en positiv elektrisk ladning, og sidstnævnte er neutrale..
Da de er agglomererede i et lille rum uden for fantasi, og ved at ladninger af det samme tegn frastøder hinanden, undrer man sig over, hvordan atomkernen forbliver sammenhængende.
Svaret ligger i andre kræfter end elektrostatisk frastødning, typisk for kernen, såsom den stærke nukleare interaktion og den svage nukleare interaktion. Disse er meget stærke kræfter, som langt overstiger den elektrostatiske kraft.
Denne form for potentiel energi kommer fra, hvordan atomer og molekyler af stoffer er arrangeret i henhold til de forskellige typer kemiske bindinger..
Når en kemisk reaktion opstår, kan denne energi omdannes til andre typer, for eksempel ved hjælp af et batteri eller et elektrisk batteri.
Potentiel energi er til stede i dagligdagen på mange måder. At observere dens virkninger er lige så let som at placere ethvert objekt i en bestemt højde og være sikker på, at det kan rulle eller falde når som helst.
Her er nogle manifestationer af de typer potentiel energi, der tidligere er beskrevet:
-Rutsjebaner
-Biler eller kugler, der ruller ned ad bakke
-Buer og pile
-Elektriske batterier
-Et urpendul
-Sving på en gynge
-Hop på en trampolin
-Brug en indtrækkelig pen.
Se: potentielle energieksempler.
Den potentielle energi afhænger af kraftens arbejde, og dette afhænger igen ikke af banen, så det kan siges at:
-Hvis A og B er to punkter, er arbejdet WAB nødvendigt for at gå fra A til B er lig med det arbejde, der er nødvendigt for at gå fra B til A. Derfor: WAB = WBA, så:
WAB + WBA = 0
-Og hvis to forskellige baner 1 og 2 forsøges at forbinde de nævnte punkter A og B, er arbejdet i begge tilfælde også det samme:
W1 = Wto.
I begge tilfælde oplever objektet en ændring i potentiel energi:
Ændring = endelig potentiel energi - indledende potentiel energi
ΔU = Uendelig - ELLERinitial = UB - ELLERTIL
Objektets potentielle energi er defineret som det negative af det arbejde, der udføres af den (konservative) kraft:
ΔU = -WAB
Men da arbejde er defineret af denne integral:
Bemærk, at enhederne af potentiel energi er de samme som arbejdets. I SI International System er enheden joule, der forkortes J og svarer til 1 newton x meter, af den engelske fysiker James Joule (1818-1889).
Andre enheder til energi inkluderer cgs erg, pund-kraft x fod, BTU (Britisk termisk enhed), kalorier og kilowatt-timer.
Lad os se nedenfor nogle særlige tilfælde af, hvordan man beregner potentiel energi.
I nærheden af jordoverfladen peger tyngdekraften lodret nedad, og dens størrelse er givet ved ligningen Vægt = masse x tyngdekraft.
Betegnelse af den lodrette akse med bogstavet "y" og tildeling til denne retning af enhedsvektoren j, positiv op og negativ ned, ændringen i potentiel energi, når en krop bevæger sig fra y = yTIL så længe y = yB det er:
U (y) = mgy
Hookes lov fortæller os, at kraften er proportional med deformationen:
F = -k.x
Her x er deformationen og k er en egenkonstant af fjederen, som indikerer, hvor stiv den er. Gennem dette udtryk beregnes den elastiske potentielle energi under hensyntagen til det jeg er enhedsvektoren i vandret retning:
U (x) = ½ kxto
Når du har et punkt elektrisk ladning Q, producerer det et elektrisk felt, der opfatter en anden punktladning hvad, og at det fungerer på det, når det flyttes fra en position til en anden midt i marken. Den elektrostatiske kraft mellem to punktsladninger har en radial retning symboliseret ved enhedsvektoren r:
En fjeder, hvis konstant er k = 10,0 N / cm strækker sig oprindeligt 1,00 cm fra dens ligevægtslængde. Du bliver bedt om at beregne den ekstra energi, der kræves for at strække fjederen op til 5,00 cm ud over dens ligevægtslængde..
Ved direkte at erstatte x = 1,00 cm i ligningen for U (x) får vi N.cm, men centimeterne skal konverteres til meter for at opnå energien i joule:
U (1) = 0,5 x 10,0 N / cm x (1,00 cm)to = 5 N. cm = 0,05 J; U (5) = 0,5 x 10,0 N / cm x (5,00 cm)to = 125 N.cm = 1,25 J
Derfor er den energiforskel, der søges, 1,25 - 0,05 J = 1,20 J.
En lille blok frigøres fra hvile fra punkt A for at glide langs den friktionsfri buede rampe til punkt B. Derfra kommer den ind i en lang ru vandret overflade med en dynamisk friktionskoefficient μk = 0,2. Find hvor langt fra punkt B det stopper, forudsat at hTIL= 3m.
Når blokken er i en højde hTIL Med hensyn til jorden har den tyngdekraftenergi på grund af dens højde. Når den frigives, omdannes denne potentielle energi gradvist til kinetisk energi, og når den glider ned ad den glatte buede rampe, øges dens hastighed..
Under stien fra A til B kan ligningerne af ensartet varieret retlinet bevægelse ikke anvendes. Selvom tyngdekraften er ansvarlig for blokens bevægelse, er den bevægelse, den oplever, mere kompleks, fordi banen ikke er retlinet.
Da tyngdekraften er en konservativ kraft, og der ikke er nogen friktion på rampen, kan du bruge bevarelsen af mekanisk energi til at finde hastigheden i slutningen af rampen:
Mekanisk energi i A = Mekanisk energi i B
m.g.hTIL + ½ m.vTILto = m.g.hB + ½ m.vBto
Udtrykket forenkles ved at bemærke, at massen vises i hvert udtryk. Det frigøres fra hvile vTIL = 0. Og hB er på jordoverfladen, hB = 0. Med disse forenklinger reduceres udtrykket til:
vBto = ghTIL
Nu begynder blokken sin rejse i den grove sektion med denne hastighed og stopper endelig ved punkt C. Derfor vC = 0. Mekanisk energi bevares ikke længere, fordi friktion er en dissipativ kraft, der har udført arbejde på blokken givet af:
Wrøre ved = - friktionskraft x tilbagelagt afstand
Dette værk har et negativt tegn, da den kinetiske friktion bremser objektet og modsætter sig dets bevægelse. Størrelsen af den kinetiske friktion Fk det er:
Fk = μk .N
Hvor N er størrelsen af den normale kraft. Den normale kraft udøves af overfladen på blokken, og da overfladen er helt vandret, afbalancerer den vægten P = mg, derfor er størrelsen af det normale:
N = mg
Hvilket fører til:
Fk = μk .mg
Det arbejde, der Fk gør ved blokken er: Wk = - fk .D = - μk .mg.D.
Dette arbejde svarer til ændring i mekanisk energi, beregnet således:
Mekanisk energi i C - Mekanisk energi i B =
ΔEm = (UC +KC) - (ELLERB + KB) = - μk .mg.D
I denne ligning er der nogle udtryk, der forsvinder: KC = 0, da blokken stopper ved C og U også forsvinderC = UB, fordi disse punkter er på jordoverfladen. Forenklingen resulterer i:
- KB = - μk .m.g. D.
½ m.vBto = μk .m.g. D.
Massen annullerer igen, og D kan opnås som følger:
D = (½ vBto) / (μk . g) = (½ vBto) / (μk . g) = (½g.hTIL) / (μk . g) = (½hTIL) / μk = 0,5 x 3 m / 0,2 = 7,5 m
Endnu ingen kommentarer