
Translationsligevægtsbetingelser, eksempler, øvelser
Et objekt hævdes at være i translationel ligevægt når summen af de kræfter, der virker på den, er nul. Dette betyder ikke, at der nødvendigvis er hvile, men bevægelsen, hvis den findes, ville være ensartet retlinet eller udelukkende roterende i tilfælde af et stort objekt..
Betingelserne for mekanisk ligevægt er baseret på Newtons mekaniske love. Faktisk fortæller den første lov os, at et objekt er i ro eller bevæger sig med ensartet retlinet bevægelse MRU, forudsat at ingen nettokraft virker på det.

Nu er nettokraften eller den resulterende kraft simpelthen vektorsummen af alle de kræfter, der virker på objektet. Ifølge Newtons anden lov skal denne sum være lig med produktet mellem massen og accelerationen, men hvis objektet ikke accelereres, forsvinder denne sum.
Og i mangel af acceleration er der de to ovennævnte muligheder: kroppen er i ro, det vil sige, den bevæger sig ikke, eller hvis den gør det, skal den være med MRU. I det første tilfælde taler vi om statisk tværnational ligevægt og i det andet dynamisk.
Translationsligevægt er en vigtig faktor i mange tekniske aspekter, for eksempel inden for byggeri. De elementer, der udgør en bygning: bjælker, kabler, rammer og mere, skal være i balance for at garantere kabinets stabilitet.
Translationsbalance søges også i mobile strukturer såsom rulletrapper, transportbånd og i udøvelsen af adskillige sportsgrene..
Artikelindeks
- 1 Betingelse for translationel ligevægt
- 1.1 Diagrammer over frit legeme
- 2 Eksempler på translationel ligevægt
- 2.1 Bygninger og veje
- 2.2 Bøger og genstande i hylderne
- 2.3 Møblerne
- 2.4 Trafiklys
- 2.5 Offentlig belysning
- 3 Øvelse løst
- 3.1 Løsning
- 4 Referencer
Translationsligevægtstilstand
Antag at flere kræfter virker på en krop, som vi betegner som F1, Fto, F3... . Fn, ved hjælp af fed skrift for at fremhæve det faktum, at kræfter er vektorer og skal tilføjes som sådan.
Vektorsummen af alle disse kræfter kaldes resulterende kraft eller nettokraft. Hvis denne summering resulterer i nulvektoren, er betingelsen for den translationelle ligevægt opfyldt:
F1+ Fto+ F3... .+ Fn = 0
Denne betingelse kan skrives kompakt ved hjælp af summeringsnotation:
∑ Fjeg = 0
Med hensyn til komponenterne i den resulterende kraft kan ovenstående ligning, som er vektor, opdeles i tre skalære ligninger, en for hver komponent af den resulterende kraft:
∑ Fix = 0; ∑ FY = 0 og ∑ Fz = 0
I praksis er det ikke let at annullere summen af kræfter, fordi friktion er en kontaktkraft mellem overflader, der næppe helt annulleres af nogen anden kraft..
Dette er grunden til, at virkelige objekter næsten aldrig er undtaget fra eksterne kræfter, og som en konsekvens er det vanskeligt at opnå translationel ligevægt.
Så ingeniører bruger mekanismer til at reducere friktion, såsom lejer og brugen af smøreolier..
Diagrammer med fri krop
Diagrammet for frit legeme er et diagram, hvor de kræfter, der virker på kroppen, er tegnet. Når man søger translationel ligevægt, skal disse kræfter være afbalancerede. For eksempel, hvis en lodret kraft rettet nedad virker, såsom vægt, så skal der være en opadgående lodret kraft, der har nøjagtig samme størrelse.
Denne kraft kan leveres af den hånd, der understøtter genstanden, så den ikke falder ned, et reb eller simpelthen overfladen på et bord.
Hvis der er en kraft, der tangerer overfladen, såsom kinetisk eller statisk friktion, skal der være en anden modsatrettende kraft for at balance kan eksistere. Lad os for eksempel se på vægten, der hænger i strengene vist i den følgende figur.
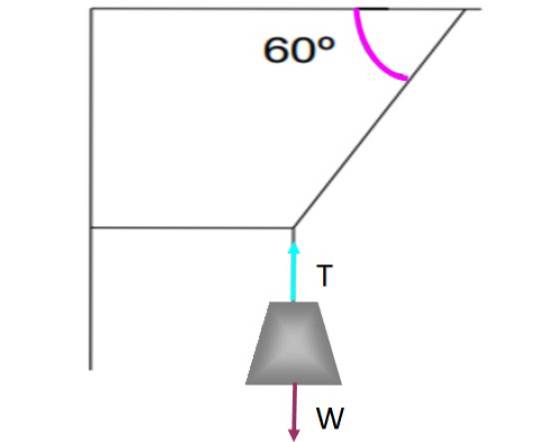
Vægten holdes i translationel balance og uden at bevæge sig takket være det lodrette reb, der holder det ved at udøve en spænding T der kompenserer for vægten W. Hver kraft er blevet repræsenteret på vægten af en pil, hver af samme størrelse og med samme retning, men modsat retning..
Balanceringskraften
Antag at et sæt kræfter virker på et objekt. Dette kaldes en kraft system hvorfra den resulterende kan findes som forklaret ovenfor: ved vektorisk tilføjelse af hver af systemets kræfter.
Nå kaldes den modsatte kraft til denne resulterende afbalanceringskraft. Hvis den resulterende kraft er FR og afbalanceringskraften er OG, derefter:
OG + FR = 0
Derfor:
OG = - FR
Eksempler på translationel ligevægt
Mange genstande, som vi finder dagligt, i og uden for hjemmet, er i translationel ligevægt:
Bygninger og veje
Bygninger og veje er bygget til at forblive stabile og ikke vælte eller kollapse. I skyskrabere og generelt meget høje bygninger er det dog nødvendigt med en vis fleksibilitet for at modstå vindens handling..
Bøger og genstande i hylderne
Bøger i et bibliotek og produkter i butikshylderne er genstande, der forbliver i translationel ligevægt og ikke bevæger sig..
Møblerne
Møblerne, fladskærms-tv og billederne på væggen samt lamperne, der hænger fra loftet, for at nævne nogle få genstande, er i translationel balance..
Trafiklys
Trafiklyset er fastgjort med stænger og kabler, så de ikke falder ned. Alligevel ved vi, at vinden får dem til at svinge.
Offentlig belysning
Gadelysene er også i translationel balance, fastgjort på lygtepælene, ligesom gadebelysningen i hovedbilledet..
Træning løst
Hvor stor skal kraften Fs med statisk friktion, så kassen i figuren forbliver i ro midt i det skrå plan i en vinkel α på 37º? Kassens masse er m = 8 kg.
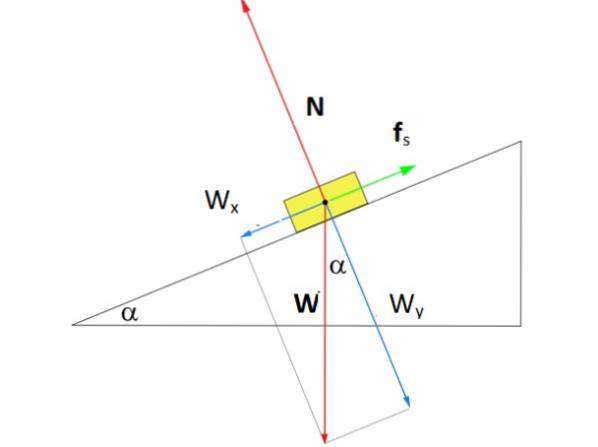
Opløsning
Figuren viser diagrammet til fri krop af kassen på planet. Der er tre kræfter, der virker på det: vægt W, rettet lodret nedad, det normale N, som er den vinkelrette kraft, der udøves af overfladen af planet på kassen, og endelig den statiske friktionskraft Fs der er imod, at kassen glider ned ad bakke.
Den translationelle ligevægtstilstand siger, at:
W + N + Fs = 0
Men vi skal huske, at dette er en vektorsum, og for at udføre det er det nødvendigt at nedbryde kræfterne i komponenter langs koordinatakserne.
På figuren er der trukket et koordinatsystem, hvor x-aksen løber parallelt med overfladen af det skrå plan. Med dette valg falder den statiske friktion på aksen, mens normal er på y-aksen. Vægt er den eneste kraft, der er skråt og skal nedbrydes ved hjælp af trigonometri:
Wx = W. sin α
WY = W. cos α
Summen af kræfter langs hver akse er:
∑ FY = N - WY = 0
∑ Fx = fs - Wx = 0
Fra denne sidste ligning følger det, at:
Fs = Wx
Og som Wx = W. sin α og størrelsen af vægten til gengæld er W = m.g, hvor g er tyngdekraftsværdien, så er størrelsen af den statiske friktion simpelthen:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / sto × sin 37º = 47,2 N.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 2. dynamik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Ed. Cengage Learning.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.



Endnu ingen kommentarer