
Termiske ligevægtsligninger, applikationer, øvelser
Den termiske ligevægt i to legemer, der er i termisk kontakt, er den tilstand, der nås efter en tid, der er lang nok til, at temperaturen i begge legemer kan udligne.
I termodynamik forstås termisk kontakt mellem to legemer (eller to termodynamiske systemer) som en situation, hvor legemerne har mekanisk kontakt eller er adskilt, men i kontakt med en overflade, der kun tillader passage af varme fra det ene legeme til det andet (diatermisk overflade).
-

Figur 1. Efter et stykke tid vil isen og drikken nå deres termiske ligevægt. Kilde: Pixabay
Ved termisk kontakt må der ikke være nogen kemisk reaktion mellem systemerne i kontakt. Der bør kun være varmeveksling.
Daglige situationer, hvor der er varmeudveksling, opstår med systemer som den kolde drik og glasset, den varme kaffe og teskeen eller kroppen og termometeret, blandt mange andre eksempler..
Artikelindeks
- 1 Hvornår er to eller flere systemer i termisk ligevægt??
- 2 Ligninger af termisk ligevægt
- 2.1 Ligevægtstemperatur
- 2.2 Termisk kontakt med faseændring
- 3 applikationer
- 3.1-Øvelse 1
- 4 Løst øvelser
- 4.1-Øvelse 2
- 4.2 Øvelse 3
- 4.3-Øvelse 4
- 5 Referencer
Når to eller flere systemer er i termisk ligevægt?
Den anden lov om termodynamik siger, at varme altid går fra kroppen med den højeste temperatur til kroppen med den laveste temperatur. Varmeoverførsel ophører, så snart temperaturerne udjævnes, og tilstanden for termisk ligevægt er nået..
Den praktiske anvendelse af termisk ligevægt er termometeret. Et termometer er en enhed, der måler sin egen temperatur, men takket være termisk ligevægt kan vi kende temperaturen i andre kroppe, såsom den hos en person eller et dyr.
Kviksølvsøjletermometeret placeres i termisk kontakt med kroppen, for eksempel under tungen, og der ventes tilstrækkelig tid på, at den termiske ligevægt mellem kroppen og termometret nås, og at dets aflæsning ikke varierer yderligere.
Når dette punkt er nået, er termometerets temperatur den samme som kroppens.
Nul loven om termodynamik siger, at hvis et legeme A er i termisk ligevægt med et legeme C, og at det samme legeme C er i termisk ligevægt med B, så er A og B i termisk ligevægt, selv når der ikke er nogen termisk kontakt mellem A og B.
Derfor konkluderer vi, at to eller flere systemer er i termisk ligevægt, når de har den samme temperatur.
Termiske ligevægtsligninger
Vi antager et legeme A med begyndelsestemperatur Ta i termisk kontakt med et andet legeme B med starttemperatur Tb. Vi antager også, at Ta> Tb, så overføres i henhold til den anden lov varmen fra A til B.
Efter et stykke tid vil termisk ligevægt blive nået, og begge legemer vil have den samme endelige temperatur Tf. Dette vil have en mellemværdi ved Ta og Tb, det vil sige Ta> Tf> Tb.
Mængden af varme Qa overført fra A til B vil være Qa = Ma Ca (Tf - Ta), hvor Ma er massen af legeme A, Ca varmekapaciteten pr. Enhedsenhed af A og (Tf - Ta) temperaturforskellen. Hvis Tf er mindre end Ta, er Qa negativ, hvilket indikerer, at kroppen A giver op varmen.
Tilsvarende for kroppen B har vi, at Qb = Mb Cb (Tf - Tb); og hvis Tf er større end Tb, så er Qb positiv, hvilket indikerer, at legeme B modtager varme. Da krop A og krop B er i termisk kontakt med hinanden, men isoleret fra miljøet, skal den samlede mængde varme, der udveksles, være nul: Qa + Qb = 0
Derefter Ma Ca (Tf - Ta) + Mb Cb (Tf - Tb) = 0
Ligevægtstemperatur
Udvikling af dette udtryk og løsning af temperaturen Tf opnås den endelige temperatur for termisk ligevægt.
-

Figur 2. Endelig ligevægtstemperatur. Kilde: selvfremstillet
Tf = (Ma Ca Ta + Mb Cb Tb) / (Ma Ca + Mb Cb).
Overvej som et bestemt tilfælde, at organerne A og B er identiske i masse og varmekapacitet, i dette tilfælde vil ligevægtstemperaturen være:
Tf = (Ta + Tb) / 2 ↔ hvis Ma = Mb og Ca = Cb.
Termisk kontakt med faseændring
I nogle situationer sker det, at når to kroppe placeres i termisk kontakt, forårsager varmevekslingen ændring af tilstand eller fase i en af dem. Hvis dette sker, skal det tages i betragtning, at der under faseændringen ikke er nogen temperaturændring i kroppen, der ændrer dens tilstand.
Hvis der forekommer faseændring af nogen af legemerne i termisk kontakt, anvendes begrebet latent varme L, som er den energi pr. Masseenhed, der er nødvendig for tilstandsændringen:
Q = L ∙ M
For eksempel er det nødvendigt at smelte 1 kg is ved 0 ° C, 333,5 kJ / kg, og denne værdi er den latente varme L for smeltning af is.
Under smeltning skifter det fra fast vand til flydende vand, men det vand holder den samme temperatur som is under smeltningsprocessen..
Ansøgninger
Termisk balance er en del af det daglige liv. Lad os for eksempel undersøge denne situation detaljeret:
-Øvelse 1
En person ønsker at bade i varmt vand ved 25 ° C. I en spand anbringes 3 liter koldt vand ved 15 ° C og i køkkenet opvarmes vand op til 95 ° C.
Hvor mange liter varmt vand skal du føje til spanden koldt vand for at få den ønskede endelige temperatur?
Opløsning
Antag at A er koldt vand og B er varmt vand:
-
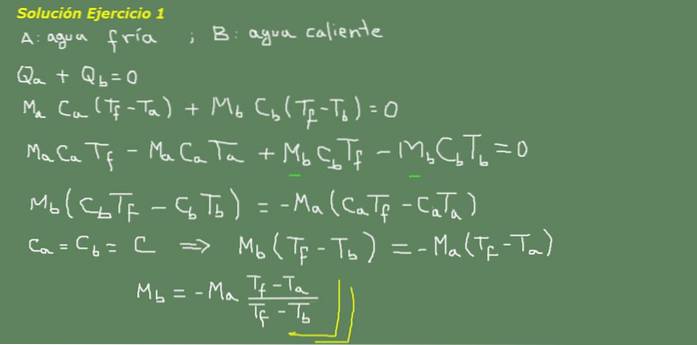
Figur 3. Løsning til øvelse 3. Kilde: egen uddybning.
Vi foreslår ligningen af termisk ligevægt, som angivet på tavlen i figur 3, og derfra løser vi massen af vand Mb.
Den indledende masse af koldt vand kan opnås, fordi vandets densitet er kendt, hvilket er 1 kg pr. Liter. Vi har 3 kg koldt vand.
Ma = 3 kg
Derefter
Mb = - 3 kg * (25 ° C - 15 ° C) / (25 ° C - 95 ° C) = 0,43 kg
Derefter er 0,43 liter varmt vand nok til endelig at opnå 3,43 liter varmt vand ved 25 ° C.
Løst øvelser
-Øvelse 2
Et stykke metal med en masse på 150 g og en temperatur på 95 ° C indføres i en beholder indeholdende en halv liter vand ved en temperatur på 18 ° C. Efter et stykke tid opnås den termiske ligevægt, og temperaturen på vandet og metallet er 25 ° C.
Antag at beholderen med vandet og metalstykket er en lukket termokande, der ikke tillader varmeudveksling med miljøet.
Få metalets specifikke varme.
Opløsning
Først beregner vi varmen absorberet af vandet:
Qa = Ma Ca (Tf - Ta)
Qa = 500g 1cal / (g ° C) (25 ° C - 18 ° C) = 3500 kalorier.
Det er den samme varme, der gives af metallet:
Qm = 150 g Cm (25 ° C - 95 ° C) = -3500 kalorier.
Så vi kan få metalets varmekapacitet:
Cm = 3500 cal / (150g 70 ° C) = ⅓ cal / (g ° C).
Øvelse 3
Du har 250 c.c. vand ved 30 ° C. Til det vand, der er i en isolerende termokande, tilsættes 25 g isterninger ved 0 ° C med det formål at afkøle det.
Bestem ligevægtstemperaturen; det vil sige temperaturen, der forbliver, når al isen er smeltet, og isvandet er opvarmet til at matche det, der er i vandet i glasset i starten.
Løsning 3
Denne øvelse kan løses i tre faser:
- Den første er smeltning af is, der absorberer varme fra det oprindelige vand for at smelte og blive til vand..
- Derefter beregnes temperaturfaldet i det oprindelige vand på grund af det faktum, at det har givet op varme (Qced<0) para fundir el hielo.
- Endelig skal det smeltede vand (kommer fra isen) afbalanceres termisk med det vand, der oprindeligt eksisterede..
-

Figur 4. Løsning til øvelse 3. Kilde: egen uddybning.
Lad os beregne den nødvendige varme til smeltning af is:
Qf = L * Mh = 333,5 kJ / kg * 0,025 kg = 8,338 kJ
Derefter er varmen fra vandet til at smelte isen Qced = -Qf
Denne varme, der afgives af vandet, sænker temperaturen til en værdi T ', som vi kan beregne som følger:
T '= T0 - Qf / (Ma * Ca) = 22,02 ° C
Hvor Ca er vandets varmekapacitet: 4,18 kJ / (kg ° C).
Endelig vil den oprindelige vandmasse, der nu er ved 22.02 ° C, opgive varmen til massen af smeltet vand fra isen, der er ved 0 ° C..
Endelig nås ligevægtstemperaturen Te efter tilstrækkelig tid:
Te = (Ma * T '+ Mh * 0 ° C) / (Ma + Mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).
Endelig opnå ligevægtstemperaturen:
Te = 20,02 ° C.
-Øvelse 4
En 0,5 kg klump bly kommer ud af ovnen ved en temperatur på 150 ° C, hvilket er et godt stykke under dets smeltepunkt. Dette stykke placeres i en beholder med 3 liter vand ved stuetemperatur på 20 ° C. Bestem den endelige ligevægtstemperatur.
Beregn også:
- Mængden af varme leveret af bly til vand.
- Mængden af varme absorberet af vand.
Data:
Specifik blyvarme: Cp = 0,03 cal / (g ° C); specifik vandvarme: Ca = 1 cal / (g ° C).
Opløsning
Først bestemmer vi den endelige ligevægtstemperatur Te:
Te = (Ma Ca Ta + Mp Cp Tp) / (Ma Ca + Mp Cp)
Te = 20,65 ° C
Derefter er mængden af varme, der frigives af bly:
Qp = Mp Cp (Te - Tp) = -1,94 x 103 cal.
Mængden af varme, der absorberes af vandet, vil være:
Qa = Ma Ca (Te - Ta) = + 1,94 x 10³ kal.
Referencer
- Atkins, s. 1999. Fysisk kemi. Omega-udgaver.
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6.… Ed Prentice Hall.
- Hewitt, Paul. 2012. Konceptuel fysik. 5. plads Ed. Pearson.
- Resnick, R. (1999). Fysisk. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- Rex, A. 2011. Grundlæggende fysik. Pearson.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.



Endnu ingen kommentarer