
Tilfældig fejlformel og ligninger, beregning, eksempler, øvelser
Det tilfældig fejl af en fysisk størrelse består af de uforudsigelige variationer af målene for den mængde. Disse variationer kan produceres af det fænomen, der måles, af måleinstrumentet eller af observatøren selv..
En sådan fejl skyldes ikke, at der er gjort noget forkert under eksperimentet, men er en fejl, der er forbundet med måleprocessen eller det fænomen, der undersøges. Dette får den målte størrelse til at være nogle gange lidt højere og nogle gange lidt mindre, men den svinger normalt omkring en central værdi..
I modsætning til tilfældig fejl kan systematisk fejl skyldes en dårlig kalibrering eller en utilstrækkelig skalafaktor i måleinstrumentet, endda en fejl i det eksperimentelle udstyr eller en utilstrækkelig observation, der forårsager en afvigelse i samme retning..
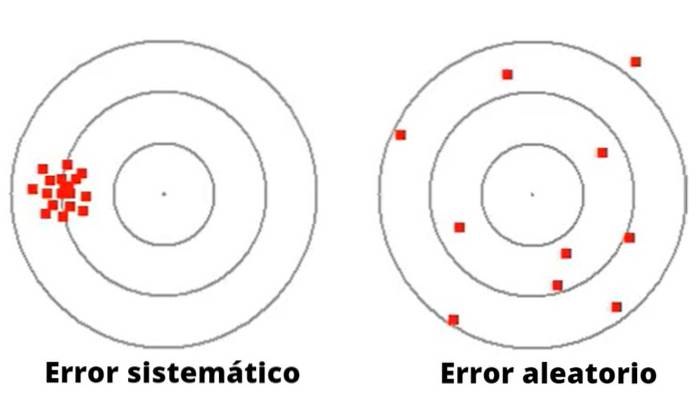
Figur 1 illustrerer forskellen mellem systematisk og tilfældig fejl i spillet med at kaste pile på et mål med cirkler..
I tilfældet med venstre er pilene koncentreret omkring et punkt langt fra centrum. Launcheren af disse pile, selvom de har et godt mål, har en systematisk fiasko, måske af visuel oprindelse eller i vejen for at kaste.
På den anden side har løfteraket til højre (i figur 1) en stor spredning omkring det centrale mål, derfor er det en meget upræcis launcher med dårligt mål, der ufrivilligt begår en tilfældig fejl..
Artikelindeks
- 1 Formler og ligninger i tilfældig fejl
- 1.1 Gennemsnitlig værdi og standardafvigelse
- 2 Sådan beregnes den tilfældige fejl?
- 3 Eksempler på tilfældig fejl
- 3.1 Måling af en længde med et målebånd eller lineal
- 3.2 Vindens hastighed
- 3.3 Når man læser lydstyrken på en gradueret cylinder
- 3.4 Når man måler et barns højde
- 3.5 Når du bruger badeværelsesvægten
- 4 Øvelse løst
- 4.1 Løsning
- 5 Referencer
Formler og ligninger i tilfældig fejl
Når tilfældig fejl observeres i måleprocessen, er det nødvendigt at gentage målingen flere gange, da set ud fra et statistisk synspunkt, jo større antallet af målinger, jo mindre er fejlen i det endelige måleoverslag..
Selvfølgelig er det i hver måling nødvendigt at passe på, at forholdene, hvorunder de udføres, altid er de samme.
Antag, at målingen gentages n gange. Da der er tilfældig fejl i hver måling, vil den have en lidt anden værdi. Antag, at sættet af n målinger er:
x1, xto, x3,..., xn
Så hvilken værdi der skal rapporteres til foranstaltningen?
Gennemsnits værdi og standardafvigelse
Det middelværdi eller gennemsnit af det sæt foranstaltninger, som vi betegner med
Standardafvigelse
Dette resultat har dog en fejlmargin givet af standardafvigelsen. For at definere det skal du først kende afvigelsen og derefter variansen:
-Afvigelse djeg hvad hver målte værdi har xi med hensyn til gennemsnitsværdien
djeg = xjeg -
Hvis gennemsnittet af afvigelserne blev beregnet, ville det systematisk blive opnået
= [(x1 -
-Gennemsnittet af afvigelserne er ikke nyttigt for at kende målingernes spredning. På den anden side er gennemsnitsværdien af kvadratet af afvigelser eller varians, betegnet med σto, hvis det er.
Det beregnes efter følgende formel:
σto = (d1to + dtoto +…. + Dnto ) / (n -1)
I statistik kaldes denne mængde varians.
Og kvadratroden af variansen er kendt som standardafvigelse σ:
σ = √ [(d1to + dtoto +…. + Dnto ) / (n-1)]
Standardafvigelsen σ fortæller os, at:
1.- 68% af de foretagne målinger falder inden for intervallet [
2.- 95% af målingerne er i intervallet [
3.- 99,7% af de målte målinger er inden for området [
Sådan beregnes den tilfældige fejl?
Måleresultatet er middelværdi af n målinger angivet med
Imidlertid
ε = σ / √n
Hvor:
σ = √ [(∑ (xi -
Det endelige resultat af målingen skal rapporteres på en af følgende måder:
± σ / √n = med et konfidensniveau på 68%.± ε ± 2σ / √n = med et konfidensniveau på 95%.± 2ε ± 3σ / √n = med et konfidensniveau på 99,7%.± 3ε
Den tilfældige fejl påvirker målingens sidste signifikante tal, som generelt falder sammen med måleinstrumentets vurdering. Men hvis den tilfældige fejl er meget stor, kan de to sidste signifikante cifre blive påvirket af variation..
Eksempler på tilfældig fejl
Tilfældige fejl kan forekomme i forskellige tilfælde, hvor en måling udføres:
Måling af en længde med et målebånd eller lineal
Når en længde måles med en lineal eller målebånd, og aflæsningerne falder mellem mærkerne på skalaen, estimeres den mellemliggende værdi.
Undertiden har estimatet et overskud og andre gange en defekt, således at tilfældig fejl introduceres i måleprocessen.

Vindens hastighed
Ved måling af vindhastighed kan der være ændringer i aflæsningen fra et øjeblik til et andet på grund af fænomenets skiftende natur..
Når du læser lydstyrken på en gradueret cylinder
Når lydstyrken læses med en gradueret cylinder, og endda forsøger at minimere parallaksfejlen, ændres observationsvinklen for menisken lidt, hver gang den måles, hvorfor målingerne påvirkes af tilfældig fejl.

Når du måler et barns højde
Når man måler et barns højde, især hvis han er lidt rastløs, foretager små ændringer i kropsholdning lidt aflæsningen.
Når du bruger vægten på badeværelset
Når vi vil måle vores vægt med en badeværelsesvægt, kan en lille ændring i omdrejningspunktet, endda en ændring i kropsholdning tilfældigt påvirke målingen..
Træning løst
En legetøjsvogn har lov til at rulle ned ad et lige og skråt spor, og den tid det tager at rejse hele sporet måles med et stopur.
Målingen udføres 11 gange, idet man sørger for altid at frigøre vognen fra samme sted uden at give den nogen impuls og holde hældningen fast..
Sættet af opnåede resultater er:
3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s, 3.03s
Hvad er målingernes tilfældige fejl?

Opløsning
Som du kan se, er de opnåede resultater ikke unikke og varierer lidt..
Den første ting er at beregne den gennemsnitlige værdi af nedstigningstiden og opnå 3.074545455 sekunder.
Det giver ikke mening at beholde så mange decimaler, da hver måling har tre signifikante tal, og den anden decimal for hver måling er usikker, da den er ved grænsen for stopurets forståelse, hvorfor resultatet afrundes til to decimaler:
Med lommeregneren i statistisk tilstand er standardafvigelsen σ = 0,03 s og standardfejlen er σ / √11 = 0,01 s. Det endelige resultat udtrykkes således:
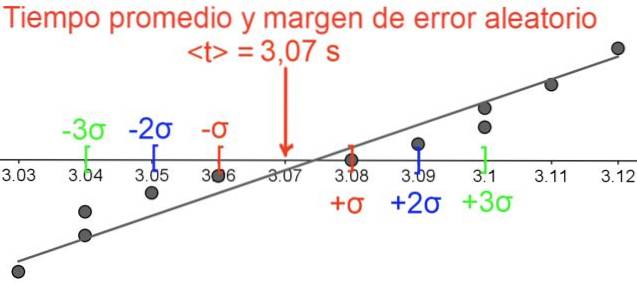
Nedstigningstid
3,08 s ± 0,01 s (med et konfidensniveau på 68%)
3,08 s ± 0,02 s (med et 95% konfidensniveau)
3,08 s ± 0,03 s (med et konfidensniveau på 99,7%)
Referencer
- Canavos, G. 1988. Sandsynlighed og statistik: Anvendelser og metoder. Mcgraw bakke.
- Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
- Helmenstine A. Tilfældig fejl vs. systematisk fejl. Gendannet fra: thoughtco.com
- Laredo, E. Fejl i medierne. Gendannet fra: usb.ve.
- Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.


Endnu ingen kommentarer