
Trækspændingsformel og ligninger, beregning, øvelser
Det Stressbelastning Det defineres som den kraft, der er vinkelret på arealet pr. Arealeenhed, der påføres en genstand i dens ender for at udøve trækkraft på den, takket være hvilken den forlænges. Dens dimensioner er kraft / areal og i matematisk form kan vi udtrykke det således:
τ = F / A
Anstrengelsesenheden i det internationale enhedssystem er den samme som den, der anvendes til tryk: pascal, forkortet Pa, hvilket svarer til 1 newton / mto.

I spændingsindsatsen er der to kræfter, der påføres i samme retning og modsatte retninger, som strækker kroppen. Hvis oprindeligt længden af objektet var Leller, ved anvendelse af trækspændingen er den nye længde L og strækningen ΔL beregnes ved:
ΔL = L - Leller
Faste objekter har elasticitet i større eller mindre grad, hvilket betyder, at når trækspændingen forsvinder, vender de tilbage til deres oprindelige dimensioner..
Dette sker, så længe stress ikke er så stort, at det forårsager permanent deformation. Gummi-, gummi- eller gummimaterialer er gode til fremstilling af elastiske genstande, og hår og hud har blandt andet denne kvalitet..
Artikelindeks
- 1 Sil
- 2 Hvordan beregnes trækspænding? (Eksempler)
- 2.1 Beregningseksempel
- 3 Løst øvelser
- 4 - Øvelse 1
- 5 - Øvelse 2
- 6 Referencer
Enhedsdeformation
Når man studerer, hvordan kroppe deformeres under stress, er det meget praktisk at definere begrebet stamme, en dimensionsløs mængde. Stamme er betegnet med det græske bogstav δ (små bogstaver "delta") og beregnes som følger:
δ = AL / Leller
Stamme bruges til sammenlignende at evaluere deformationen af objektet under stress. Lad os se det på denne måde: at strække en 1 meter lang bjælke 1 cm er ikke det samme som at strække en 10 m lang bjælke 1 cm. I det første tilfælde er deformationen meget mere markant end i det andet.
Hvordan beregnes trækspænding? (Eksempler)
Den engelske fysiker og nutid af Newton ved navn Robert Hooke (1635-1703), undersøgte kroppens elastiske egenskaber og etablerede den lov, der bærer hans navn. Med det er den påførte spænding relateret til den deformation, der opleves, når spændingen er lille:
Stress ∝ Stamme (enhed)
Det er logisk at forvente, at jo højere trækspænding, jo større vil forlængelsen forekomme. Brug af definitionerne ovenfor:
τ ∝ δ
Den nødvendige proportionalitetskonstant for at etablere lighed er betegnet Y og er kendt som Youngs modul eller elasticitetsmodul, karakteristisk for materialer:
τ = Y⋅δ
Youngs modul har de samme trækspændingsenheder, da belastningen er dimensioneløs.
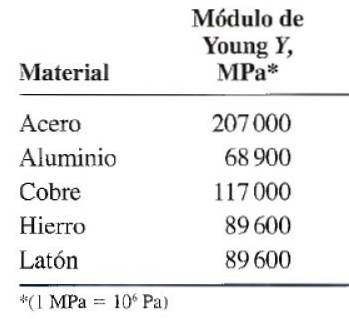
Så en måde at beregne trækspændingen på i en krop med elastiske egenskaber er at måle stammen og kende dens Youngs modul. Denne mængde er bestemt eksperimentelt for mange materialer og er opstillet i tabelform.
Beregningseksempel
Antag, at en ledning lavet af hærdet stål med en diameter på 3 mm udsættes for en trækspænding, der hænger derfra en vægt på 250 N, hvad ville være størrelsen af nævnte spænding?
Nå, vi kan bruge definitionen af trækspænding som forholdet mellem kraften vinkelret på overfladen og arealet på den overflade. Lad os først beregne arealet under forudsætning af en ledning med cirkulært tværsnit:
A = π. (d / 2)to = π. (dto / 4)
Ledningens diameter er 3 mm, og disse enheder skal omdannes til meter:
d = 3 x 10-3 m.
A = π. (3 x 10-3 m)to / 4 = 7,07 x 10-6 mto.
Trækspændingen frembringes af vægten, der hænger fra tråden, som påføres vinkelret på dens tværsnit, og derfor:
τ = 250 N / 7,07 x 10-6 mto = 3,5 x 10 7 Pa
Pascal er en ret lille enhed, så multipler er ikke usædvanlige. At vide, at 1 mega-pascal (MPa) er 106 pascal, trækspændingen forbliver:
τ = 35 MPa
Løst øvelser
- Øvelse 1
Stangens elasticitetsmodul er 4 x 10elleve Pa. Hvilken stamme opnås ved at påføre en trækspænding på 420 MPa?
Opløsning
Ligningen, der skal bruges, er:
τ = Y⋅δ
Med det beregner vi stammen:
δ = τ / Y = 420 x 106 Pa / 4 x 10elleve Pa = 0,00105
δ = AL / Leller
Derfor er stammen AL:
AL = 0,00105 Leller
Hvis f.eks. Stangen oprindeligt var 1 meter lang, strækkes den med kun 0,00105 m = 1,05 mm.
- Øvelse 2
En ståltråd er 1,50 m lang og har en diameter på 0,400 mm. Den ene ende er fastgjort til loftet, og en jordreflektor er fastgjort til den anden. m = 1,50 kg, som frigives. Beregn:
a) Trådens strækning.
b) Stamme og procentstamme. Er det muligt for ledningen at bryde under reflektorens vægt??
Opløsning
Ledningen vil strække sig, da den under ophængning af reflektoren udsættes for en trækstyrke. Kraften, der producerer denne indsats, er reflektorens vægt.
Vægten af et objekt med masse m er masseproduktet gange værdien af accelerationen på grund af tyngdekraften, derfor:
F = 1,50 kg x 9,8 m / sto = 14,7 N
Ledningens tværsnitsareal er nødvendigt:
A = π. (dto / 4) = π x (0,4 x 10-3 m) 2/4 = 1,26 x 10-7 mto.
Med disse resultater beregnes den indsats, der udøves af ledningens vægt:
τ = 14,7 N / 1,26 x 10-7 mto = 1,17 x 108 Pa
Ledningen har en elastisk opførsel, derfor er det gyldigt at antage, at Hookes lov er opfyldt:
τ = Y⋅δ
Fra tabellen over elasticitetsmodul finder vi, at for stål Y = 207 x 109 Pa. Derudover er stammen:
δ = AL / Leller
Udskiftning i ligningen for indsatsen:
τ = Y⋅δ = Y⋅ (AL / Leller)
Derfor er strækningen:
AL = Leller τ / Y =
= 1,50 m x 1,17 x 108 Pa / 207 x 109 Pa = 8,5 x 10-4 m = 0,849 mm.
Trådens stamme er:
δ = AL / Leller = 8,5 x 10-4 m / 1,5 m = 5,652 x 10-4
Hvis vi udtrykker det som en procentdel, er den procentuelle enhedsdeformation 0,0565%, mindre end 0,1%, derfor forventes det, at ledningen vil modstå vægten af reflektoren godt uden at gå i stykker, da den deformation, den oplever, ikke er for stor i sammenligning til original længde.
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Beer, F. 2010. Mekanik af materialer. McGraw Hill. 5. plads Udgave.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Valera Negrete, J. 2005. Noter om generel fysik. UNAM.



Endnu ingen kommentarer