Det millikan eksperiment, udført af Robert Millikan (1868-1953) sammen med sin studerende Harvey Fletcher (1884-1981), begyndte i 1906 og havde til formål at undersøge egenskaberne ved elektrisk ladning og analysere bevægelsen af tusindvis af dråber olie midt i en uniform elektrisk felt.
Konklusionen var, at den elektriske ladning ikke havde en vilkårlig værdi, men at den kom i multipla på 1,6 x 10-19 C, som er elektronens grundlæggende ladning. Derudover blev massen af elektronen fundet.
Tidligere har fysikeren J.J. Thompson havde eksperimentelt fundet ladning-masseforholdet mellem denne elementære partikel, som han kaldte "corpuscle", men ikke værdierne for hver størrelse separat..
Fra denne ladning-masseforhold og elektronens ladning blev værdien af dens masse bestemt: 9,11 x 10-31 Kg.
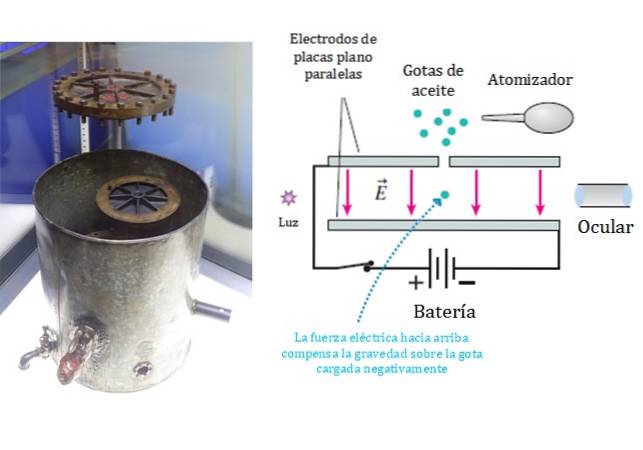
For at nå deres formål brugte Millikan og Fletcher en forstøver, hvormed en fin tåge af oliedråber blev sprøjtet. Nogle af dråberne blev ladet elektrisk på grund af friktion i dysen.
De ladede dråber satte sig langsomt ned på parallelle plane pladeelektroder, hvor nogle få passerede gennem et lille hul i den øverste plade, som vist i diagrammet i figur 1.
Inde i de parallelle plader er det muligt at skabe et ensartet elektrisk felt vinkelret på pladerne, hvis størrelse og polaritet blev styret ved at ændre spændingen..
Dråbernes opførsel blev observeret ved at belyse det indre af pladerne med et stærkt lys..
Artikelindeks
Hvis dråben har en ladning, udøver feltet skabt mellem pladerne en kraft på den, der modvirker tyngdekraften..
Og hvis det også formår at forblive ophængt, betyder det, at feltet udøver en opad lodret kraft, som nøjagtigt afbalancerer tyngdekraften. Denne betingelse afhænger af værdien af hvad, byrden ved dråben.
Millikan bemærkede faktisk, at nogle dråber blev suspenderet efter at have vendt om på marken, andre begyndte at stige eller fortsatte med at stige ned.
Ved at justere værdien af det elektriske felt - f.eks. Ved hjælp af en variabel modstand - kunne der drages et fald til at forblive ophængt inden i pladerne. Selv om det i praksis ikke er let at opnå, hvis det sker, vil kun den kraft, der udøves af marken og tyngdekraften, virke på faldet..
Hvis dråbens masse er m og dens belastning er hvad, vel vidende at kraften er proportional med det anvendte størrelsesfelt OG, Newtons anden lov siger, at begge kræfter skal afbalanceres:
mg = q.E
q = mg / E
Værdien af g, tyngdeacceleration er kendt såvel som størrelsen OG af feltet, hvilket afhænger af spændingen V mellem pladerne og afstanden mellem dem L, Hvad:
E = V / L.
Spørgsmålet var at finde massen af den lille dråbe olie. Når dette er opnået, skal du bestemme belastningen hvad det er fuldt ud muligt. Naturligvis det m Y hvad er henholdsvis massen og ladningen af oliedråben, ikke elektronen.
Men ... faldet er ladet, fordi det mister eller vinder elektroner, så dets værdi er relateret til ladningen af partiklen.
Millikan og Fletchers problem var at bestemme massen af en dråbe, ikke en let opgave på grund af dens lille størrelse..
At kende densiteten af olien, hvis massen af dråben er, kan massen løses. Men lydstyrken var også meget lille, så konventionelle metoder var ikke nyttige..
Forskerne vidste imidlertid, at sådanne små genstande ikke falder frit, da luftens eller miljøets modstand griber ind ved at bremse deres bevægelse. Selvom partiklen, når den frigives med marken slukket, oplever en accelereret lodret bevægelse og nedad, ender den med at falde med konstant hastighed..
Denne hastighed kaldes "terminalhastighed" eller "begrænsende hastighed", som i tilfælde af en kugle afhænger af dens radius og luftens viskositet..
I mangel af et felt målte Millikan og Fletcher den tid det tog for dråberne at falde. Forudsat at dråberne var sfæriske og med værdien af luftens viskositet, lykkedes det dem at bestemme radius indirekte ud fra terminalhastigheden.
Denne hastighed findes ved at anvende Stokes 'lov, og her er dens ligning:
-vt er terminalhastigheden
-R er faldets radius (sfærisk)
-η er luftens viskositet
-ρ er tætheden af dråben
Millikans eksperiment var afgørende, fordi det afslørede flere vigtige aspekter i fysik:
I) Elementarladningen er den elektron, hvis værdi er 1,6 x 10 -19 C, en af de grundlæggende konstanter for videnskaben.
II) Enhver anden elektrisk ladning kommer i multipla af den grundlæggende ladning.
III) Kendskab til elektronens ladning og forholdet mellem ladning og masse af J.J. Thomson, det var muligt at bestemme elektronens masse.
III) På niveauet af partikler så små som elementære partikler er tyngdevirkningerne ubetydelige sammenlignet med elektrostatik.
Millikan modtog Nobelprisen i fysik i 1923 for disse opdagelser. Hans eksperiment er også relevant, fordi han bestemte disse grundlæggende egenskaber ved elektrisk ladning, startende fra en simpel instrumentering og anvendte love, der var velkendte for alle..
Imidlertid blev Millikan kritiseret for at have kasseret mange observationer i sit eksperiment uden nogen åbenbar grund for at reducere den statistiske fejl i resultaterne og gøre dem mere "præsentable".
Millikan målte mange, mange dråber i sit eksperiment, og ikke alle var olie. Han prøvede også kviksølv og glycerin. Som nævnt startede eksperimentet i 1906 og varede i et par år. Tre år senere, i 1909, blev de første resultater offentliggjort.
I løbet af denne periode opnåede han en række ladede dråber ved at slå røntgenstråler gennem pladerne for at ionisere luften imellem dem. På denne måde frigives ladede partikler, som dråberne kan acceptere.
Desuden fokuserede han ikke udelukkende på de ophængte dråber. Millikan observerede, at når dråberne steg op, varierede stigningshastigheden også alt efter den leverede belastning..
Og hvis dråben faldt ned, ændrede denne ekstra opladning, der blev tilføjet takket være røntgenstrålingens indgreb, ikke hastigheden, fordi enhver masse af elektroner, der blev føjet til dråben, er minimal sammenlignet med selve dråbens masse..
Uanset hvor meget ladning han tilføjede, fandt Millikan, at alle dråberne erhvervede opkræver heltal multipla af en bestemt værdi, hvilket er og, den grundlæggende enhed, som som vi har sagt er elektronens ladning.
Millikan scorede oprindeligt 1.592 x 10-19 C for denne værdi, lidt mindre end aktuelt accepteret, hvilket er 1.602 x 10-19 C. Forholdet kan have været den værdi, du gav til luftens viskositet i ligningen for at bestemme faldets terminalhastighed..
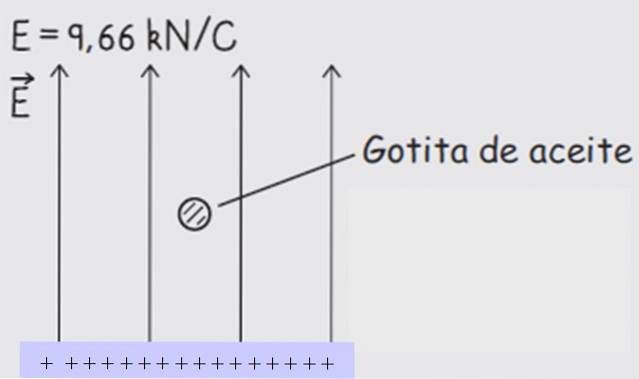
Vi ser følgende eksempel. En oliedråbe har en densitet ρ = 927 kg / m3 og frigives midt i elektroderne med det elektriske felt slukket. Dråben når hurtigt terminalhastigheden, hvorved radius bestemmes, hvis værdi viser sig at være R = 4,37 x10-7 m.
Det ensartede felt er tændt, rettet lodret opad og har styrke 9,66 kN / C. På denne måde suspenderes faldet i hvile..
Det spørger:
a) Beregn dråbeladningen
b) Find hvor mange gange den grundlæggende ladning er indeholdt i ladningens fald.
c) Bestem om muligt lastens tegn.
Tidligere blev følgende udtryk afledt for en dråbe i hvile:
q = mg / E
Ved at kende dråbens tæthed og radius bestemmes dråbens masse:
ρ = m / V.
V = (4/3) πR3
Derfor:
m = ρ.V = ρ. (4/3) πR3= 927 kg / m3. (4/3) π. (4,37 x 10-7 m)3= 3,24 x 10-16 kg
Derfor er afgiften for dråben:
q = mg / E = 3,24 x 10-16 kg x 9,8 m / sto/ 9660 N = 3,3 x 10-19 C
At vide, at den grundlæggende ladning er e = 1,6 x 10 -19 C, belastningen opnået i det foregående afsnit divideres med denne værdi:
n = q / e = 3,3 x 10-19 C /1,6 x 10 -19 C = 2,05
Resultatet er, at ladningen i faldet er ca. dobbelt så stor (n≈2) som den grundlæggende ladning. Det er ikke ligefrem dobbelt, men denne lille uoverensstemmelse skyldes den uundgåelige tilstedeværelse af eksperimentel fejl samt afrunding i hver af de tidligere beregninger..
Det er muligt at bestemme ladningens tegn takket være det faktum, at udsagnet giver information om feltets retning, som er lodret lodret opad, såvel som kraften.
Elektriske feltlinjer starter altid fra positive ladninger og slutter med negative ladninger, derfor er den nederste plade ladet med et + tegn og den øverste plade med et - tegn (se figur 3).
Da dråben er rettet mod pladen ovenfor drevet af marken, og da ladninger af det modsatte tegn tiltrækker, skal dråben have en positiv ladning.
I virkeligheden er det ikke let at opnå faldet suspenderet. Så Millikan brugte de lodrette forskydninger (op- og nedture), som faldet oplevede ved at slå marken til og fra, plus ændringer i røntgenopladning og rejsetider for at estimere, hvor meget ekstra opladning dråben havde erhvervet..
Denne erhvervede ladning er proportional med ladningen af elektronen, som vi allerede har set, og kan beregnes med stigning og faldtider, massen af faldet og værdierne af g Y OG.
Endnu ingen kommentarer