
Elektrisk feltstrøm
Hvad er elektrisk feltflux?
Det elektrisk feltstrøm eller simpelthen elektrisk flux er en skalar mængde, der er proportional med antallet af elektriske feltlinjer, der passerer gennem en overflade. Det er betegnet med det græske hovedbogstav Φ (phi).
Det elektriske felt "strømmer" faktisk ikke på den måde, som en strøm af vand gør, skønt strømmen af væsken ligner den i det elektriske felt..
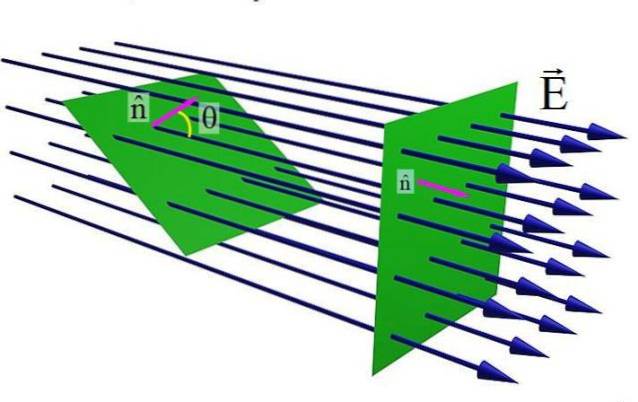
Ovenstående figur viser en flad overflade gennemkørt af et elektrisk felt OG. Når enhedsvektoren er normal til overfladen n og marken OG er parallelle, er antallet af feltlinjer, der krydser overfladen, maksimalt. Men som vinklen θ mellem n Y OG, antallet af linjer, der passerer gennem den grønne overflade, er mindre.
På den anden side afhænger den elektriske feltstrøm også af størrelsen på OG, fordi jo større dette er, jo flere feltlinjer krydser overfladen. Og selvfølgelig, jo større areal S på overfladen er, jo større strømning, så følgende ligning etableres:
Φ = E ∙ Scosθ
Dette udtryk er konsistent med prikproduktet mellem vektorerne OG Y n:
Φ = (OG • n) S
Enheden til elektrisk feltstrøm i SI International System of Units er N.mto/ C (newton x kvadratmeter / coulomb). Alternativt, da feltet også måles i V / m (volt over meter), forbliver den elektriske flux i (V ∙ m).
Eksempler
Ifølge definitionen kan den elektriske flux være positiv, negativ eller lig med 0. Den elektriske feltstrøm er:
-Positiv når vinkel θ mellem OG Y n er mindre end 90º, da cos θ er større end nul.
-Negativt, hvis nævnte vinkel er større end 90º, for så er cos less mindre end nul.
-Null når θ er nøjagtigt 90º, fordi cos 90º = 0 og feltlinjerne i dette tilfælde er tangentiale til overfladen.
-På den anden side, hvis vinklen mellem OG Y n er lig med 0, får flowet sin maksimale værdi.
Disse muligheder vises i følgende billede:
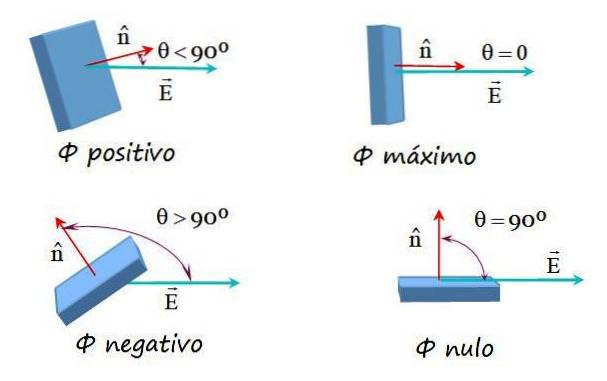
Elektrisk feltstrøm på en vilkårlig overflade
Tidligere blev den elektriske feltstrøm bestemt i det særlige tilfælde af et ensartet felt, der hælder på en plan overflade. For en overflade med vilkårlig form S og / eller et ikke-ensartet elektrisk felt, er vinklen mellem OG Y n kan variere fra punkt til punkt.
I den følgende figur er der to eksempler, til venstre en buet overflade og til højre en lukket overflade.
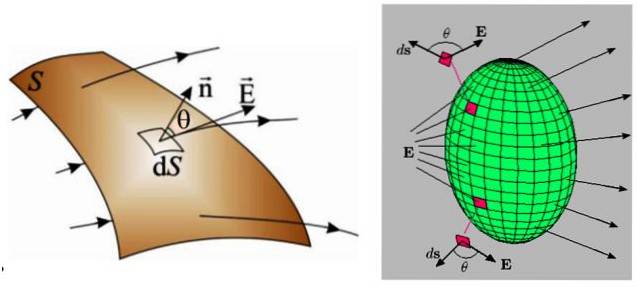
I begge tilfælde er overfladen opdelt i meget mindre regioner af uendelig størrelse, kaldet dS, gennem hvilken en strøm også uendelig lille dΦ passerer igennem:
dΦ = (OG•n) dS = (Ecosθ) dS
Det samlede felt opnås ved at tilføje alle disse infinitesimale bidrag:


I tilfælde af lukkede overflader, n peger altid udad, derfor har flowet et + tegn, når det er fremtrædende for S, da vinklen mellem OG Y n er mindre end 90º, og tegn - når feltet er indgående, for da er vinklen mellem OG Y n er større end 90º (se figur 2).
Bemærk, at i den lukkede overflade til højre er antallet af feltlinjer, der kommer ind i overfladen, lig med antallet af linjer, der forlader. Derfor er nettostrømningen, defineret som den algebraiske sum af den indgående strøm og den udgående strøm, nul.
Kilden til det elektriske felt er i dette tilfælde uden for overfladen, men nettostrømmen ville være forskellig fra 0, hvis kilden til det elektriske felt (fordelingen af ladninger) var inde i overfladen..
Uddannelse
Øvelse 1
Det har et elektrisk felt OG = 3,5 kN / C x og en flad rektangulær overflade 0,35 m bred og 0,7 m lang. Find den elektriske feltstrøm gennem rektanglet i følgende tilfælde:
a) Overfladen er parallel med yz-planet.
b) Rektanglet er parallelt med xy-planet.
c) Normalet af planet danner en vinkel på 40º med x-aksen og indeholder y-aksen.

Løsning til
Den normale vektor og den elektriske feltvektor er parallelle, derfor er vinklen θ mellem dem 0º og den elektriske flux er:
Φ = (E ∙ S) cos 0 = E ∙ S
Arealet S for rektanglet er:
S = 0,35 m x 0,7 m = 0,245 mto
Udskiftning i Φ:
Φ = E ∙ S = 3,5 x 103 N / C × 0,245 mto = 857,5 N ∙ mto / C.
Løsning b
Den elektriske feltstrøm er 0, da vektorerne OG Y n er vinkelret på hinanden.
Løsning c
Vinklen θ mellem marken OG og den normale vektor n er 40º (se figur), derfor:
Φ = E ∙ S ∙ cos θ = 3,5 x 103 N / C × 0,245 mto × cos 40º = 656,9 N ∙ mto / C.
Øvelse 2
Beregn den elektriske feltstrøm, der producerer en positiv punktladning qeller = 2μC placeret i midten af en sfære med radius R = 5 cm.
Opløsning
Feltet produceret af ladningen qeller Det er ikke ensartet, men fra Coulombs lov vides det, at det på kuglens overflade har en størrelse på:
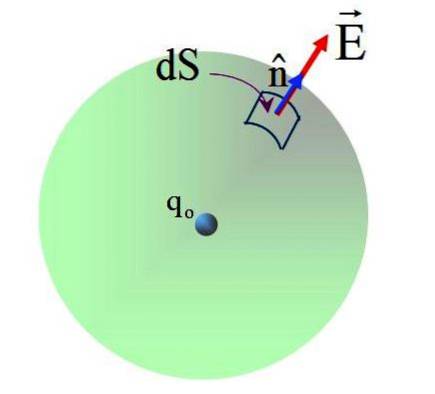

Feltet har en radial retning og den normale vektor n, derfor er vinklen mellem begge vektorer 0 på hvert punkt på den sfæriske overflade. Udskiftning i:

Det skal:

Integralet af dS over hele sfæriske overflade S er dens areal, som er 4πRto, Dermed:

Dens værdi er:
Φ = 4π × 9 × 109 x 2 × 10-6 Nmto/ C = 2,3 x 105 Nmto/ C
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Volumen 5. Elektrostatik. Redigeret af Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2. plads Ed. McGraw Hill.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1. Pearson.


Endnu ingen kommentarer