
Volumenstrøm
Hvad er volumenstrøm?
Det volumenstrøm det gør det muligt at bestemme væskevolumenet, der passerer gennem et afsnit af ledningen, og tilvejebringer et mål for den hastighed, hvormed væsken bevæger sig igennem den. Derfor er dens måling især interessant inden for så forskellige områder som blandt andet industri, medicin, byggeri og forskning..
Imidlertid er måling af en væskes hastighed (det være sig en væske, en gas eller en blanding af begge) ikke så enkel som at måle forskydningshastigheden for et fast legeme kan være. Derfor sker det, at for at kende en væskes hastighed er det nødvendigt at kende dens strømning.
Dette og mange andre spørgsmål relateret til væsker behandles af grenen af fysik kendt som væskemekanik. Flow defineres som hvor meget væske der passerer gennem en sektion af en kanal, det være sig en rørledning, en olierørledning, en flod, en kanal, en blodrør osv. Under hensyntagen til en tidsmæssig enhed.
Volumenet, der passerer gennem et givet område i en tidsenhed, beregnes normalt, også kaldet volumenstrøm. Massen eller massestrømmen, der passerer gennem et givet område på et bestemt tidspunkt, defineres også, skønt den bruges sjældnere end volumenstrøm..
Hvordan beregnes volumenstrøm?
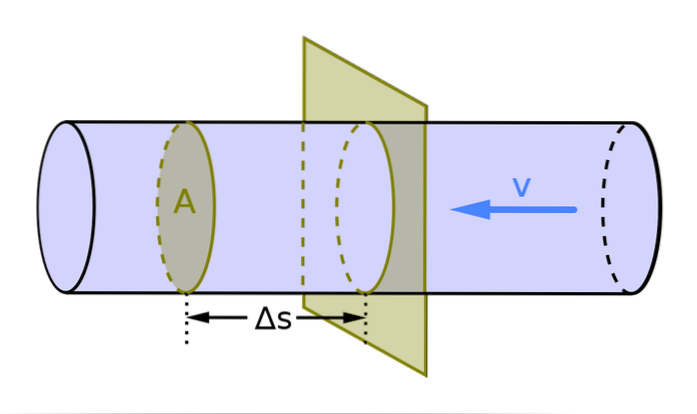
Den volumetriske strømningshastighed er repræsenteret af bogstavet Q. I de tilfælde, hvor strømningen bevæger sig vinkelret på ledersektionen, bestemmes den med følgende formel:
Q = A = V / t
I denne formel er A sektionen af lederen (det er fluidets gennemsnitlige hastighed), V er volumenet og t er tiden. Da i det internationale system måles området eller sektionen af lederen i mto og hastigheden i m / s måles flowet m3/ s.
For de tilfælde, hvor hastigheden af væskeforskydningen skaber en vinkel θ med retningen vinkelret på overfladesektionen A, er udtrykket for at bestemme strømningshastigheden følgende:
Q = A cos θ
Dette er i overensstemmelse med den tidligere ligning, da strømmen er vinkelret på området A, θ = 0 og derfor cos θ = 1.
Ovenstående ligninger gælder kun, hvis væskens hastighed er ensartet, og hvis sektionens areal er fladt. Ellers beregnes volumenstrømmen gennem følgende integral:
Q = ∫∫s v d S
I denne integrerede dS er overfladevektoren, bestemt af følgende udtryk:
dS = n dS
Der er n enhedsvektoren normal til kanaloverfladen og dS et overfladedifferentielt element.
Kontinuitetsligning
Et kendetegn ved ukomprimerbare væsker er, at væskens masse konserveres ved hjælp af to sektioner. Af denne grund er kontinuitetsligningen opfyldt, hvilket etablerer følgende forhold:
ρ1 TIL1 V1 = ρto TILto Vto
I denne ligning er ρ væskens tæthed.
For tilfælde af regimer i permanent strømning, hvor tætheden er konstant, og det derfor er korrekt, at ρ1 = ρto, koger ned til følgende udtryk:
TIL1 V1 = Ato Vto
Dette svarer til at bekræfte, at strømmen er bevaret og derfor:
Spørgsmål1 = Qto.
Af observationen af ovenstående følger det, at væsker accelererer, når de når et smallere afsnit af en kanal, mens de sænker farten, når de når et bredere afsnit af en kanal. Denne kendsgerning har interessante praktiske anvendelser, da den gør det muligt at spille med en væskes bevægelseshastighed.
Bernoullis princip
Bernoullis princip bestemmer, at for en ideel væske (det vil sige en væske, der hverken har viskositet eller friktion), der bevæger sig i cirkulation gennem en lukket ledning, forbliver dens energi konstant gennem hele dens forskydning..
I sidste ende er Bernoullis princip intet andet end formuleringen af loven om bevarelse af energi til strømmen af en væske. Bernoullis ligning kan således formuleres som følger:
h + vto / 2g + P / ρg = konstant
I denne ligning er h højden og g er accelerationen på grund af tyngdekraften.
Bernoulli-ligningen tager til enhver tid hensyn til en væskes energi, en energi bestående af tre komponenter.
- En kinetisk komponent, der inkluderer energi på grund af den hastighed, hvormed væsken bevæger sig.
- En komponent genereret af tyngdepotentialet som en konsekvens af den højde, hvormed væsken er.
- En komponent af strømningsenergi, som er den energi, en væske besidder på grund af tryk.
I dette tilfælde udtrykkes Bernoullis ligning som følger:
h ρ g + (vto ρ) / 2 + P = konstant
Logisk set, når der er tale om en rigtig væske, udtrykkes Bernoulli-ligningen ikke, da friktionstab opstår i væskeskiftet og det er nødvendigt at ty til en mere kompleks ligning.
Hvad påvirker volumenstrømmen?
Volumenstrøm påvirkes, hvis der er en blokering i kanalen.
Derudover kan volumetrisk strømningshastighed også ændre sig på grund af variationer i temperatur og tryk i den virkelige væske, der bevæger sig gennem en ledning, især hvis dette er en gas, da det volumen, som en gas optager, varierer som en funktion af temperaturen og trykket. på.
Enkel metode til måling af volumenstrøm
En virkelig enkel metode til måling af volumenstrøm er at lade en væske strømme ind i en doseringstank i et bestemt tidsrum..
Denne metode er generelt ikke særlig praktisk, men sandheden er, at det er ekstremt simpelt og meget illustrativt at forstå betydningen og vigtigheden af at kende en væskes strømningshastighed..
På denne måde får væsken lov til at strømme ind i en måletank i et tidsrum, det akkumulerede volumen måles, og det opnåede resultat divideres med den forløbne tid.
Referencer
- Flow (Fluid) (n.d.). På Wikipedia. Gendannet fra es.wikipedia.org.
- Volumetrisk strømningshastighed (n.d.). På Wikipedia. Gendannet fra en.wikipedia.org.
- Engineers Edge, LLC. "Ligning af flydende volumetrisk strømningshastighed". Ingeniører Edge
- Mott, Robert (1996). "1". Anvendt væskemekanik (4. udgave). Mexico: Pearson Education.
- Batchelor, G.K. (1967). En introduktion til væskedynamik. Cambridge University Press.
- Landau, L.D. Lifshitz, E.M. (1987). Væskemekanik. Kursus i teoretisk fysik (2. udgave). Pergamon Press.




Endnu ingen kommentarer