Absolut frekvensformel, beregning, fordeling, eksempel

Det Absolut frecuency Det defineres som antallet af gange, at de samme data gentages inden for sæt af observationer af en numerisk variabel. Summen af ​​alle de absolutte frekvenser svarer til at samle dataene.

Når du har mange værdier af en statistisk variabel, er det praktisk at organisere dem passende for at udtrække oplysninger om dens adfærd. Sådan information gives af målene for den centrale tendens og målingerne af spredning..

I beregningerne af disse mål repræsenteres dataene gennem den hyppighed, hvormed de vises i alle observationer..

Følgende eksempel viser, hvor afslørende den absolutte frekvens for hvert stykke data er. I løbet af første halvdel af maj var disse de bedst sælgende cocktailkjolestørrelser fra en velkendt tøjbutik til kvinder:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Hvor mange kjoler sælges i en bestemt størrelse, for eksempel størrelse 10? Ejere er interesserede i at vide at bestille.

Bestilling af data gør det lettere at tælle, der er nøjagtigt 30 observationer i alt, som bestilt fra den mindste størrelse til den største er som følger:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

Og nu er det tydeligt, at størrelse 10 gentages 6 gange, derfor er dens absolutte frekvens lig med 6. Den samme procedure udføres for at finde ud af den absolutte frekvens for de resterende størrelser..

Artikelindeks

• 1 Formler
  • 1.1 Andre frekvenser
• 2 Sådan får du den absolutte frekvens?
  • 2.1 Tabulering
  • 2.2 Udvidet frekvenstabel
• 3 Frekvensfordeling
  • 3.1 Frekvensfordeling for grupperede data
• 4 Eksempel
• 5 Øvelse løst
  • 5.1 Løsning
• 6 Referencer

Formler

Den absolutte frekvens, betegnet som f_jeg, er lig med antallet af gange, at en bestemt værdi X_jeg er inden for gruppen af ​​observationer.

Antages det, at det samlede antal observationer er N-værdier, skal summen af ​​alle de absolutte frekvenser være lig med dette tal:

.F_jeg = f₁ + F_to + F₃ +... f_n = N

Andre frekvenser

Hvis hver værdi af f_jeg divideret med det samlede antal data N, har vi relativ hyppighed F_r af X-værdien_jeg:

F_r = f_jeg / N

Relative frekvenser er værdier mellem 0 og 1, fordi N altid er større end nogen f_jeg, men summen skal være lig med 1.

Multiplicere hver værdi af f med 100_r du har procent relativ frekvens, hvis sum er 100%:

Procentdel relativ frekvens = (f_jeg / N) x 100%

Det er også vigtigt kumulativ frekvens F_jeg op til en bestemt observation er dette summen af ​​alle de absolutte frekvenser til og med nævnte observation:

F_jeg = f₁ + F_to + F₃ +... f_jeg

Hvis den akkumulerede frekvens divideres med det samlede antal data N, har vi kumulativ relativ hyppighed, som ganget med 100 giver procent kumulativ relativ hyppighed.

Sådan får du den absolutte frekvens?

For at finde den absolutte frekvens af en bestemt værdi, der hører til et datasæt, er de alle organiseret fra laveste til højeste, og antallet af gange værdien vises tælles.

I eksemplet med kjolestørrelser er den absolutte frekvens for størrelse 4 3 kjoler, dvs. f₁ = 3. For størrelse 6 blev der solgt 4 kjoler: f_to = 4. I størrelse 8 blev der også solgt 4 kjoler f₃ = 4 og så videre.

Tabulering

De samlede resultater kan repræsenteres i en tabel, der viser de absolutte frekvenser for hver enkelt:

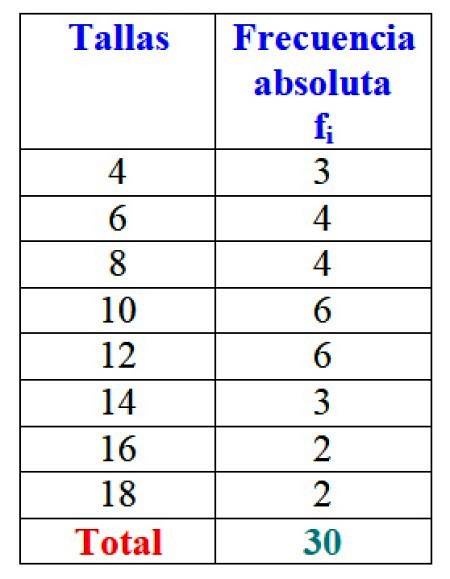
Det er åbenlyst en fordel at organisere informationen og være i stand til at få adgang til den med et øjeblik, i stedet for at arbejde med individuelle data.

Vigtig: bemærk, at når du tilføjer alle værdierne i kolonne f_jeg  du får altid det samlede antal data. Hvis ikke, skal du kontrollere regnskabet, da der er en fejl.

Udvidet frekvenstabel

Ovenstående tabel kan udvides ved at tilføje de andre frekvenstyper i på hinanden følgende kolonner til højre:

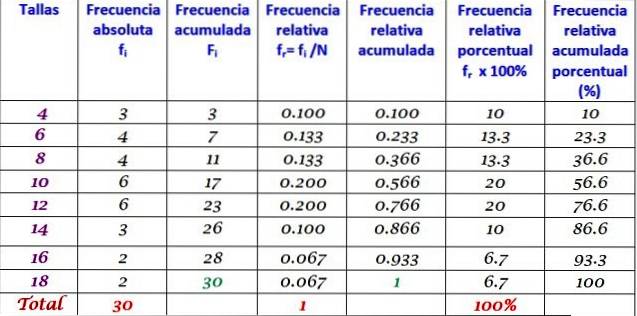
Frekvensfordeling

Frekvensfordelingen er resultatet af organisering af data med hensyn til deres frekvenser. Når du arbejder med mange data, er det praktisk at gruppere dem i kategorier, intervaller eller klasser, hver med sine respektive frekvenser: absolut, relativ, akkumuleret og procent..

Formålet med at gøre dem er lettere at få adgang til oplysningerne i dataene samt at fortolke dem korrekt, hvilket ikke er muligt, når de præsenteres i ingen rækkefølge..

I eksemplet med størrelser er dataene ikke grupperet, da de ikke er for mange størrelser og let kan manipuleres og redegøres for. Kvalitative variabler kan også arbejdes på denne måde, men når dataene er meget talrige, er det bedre at arbejde ved at gruppere dem i klasser.

Frekvensfordeling for grupperede data

For at gruppere dine data i klasser af samme størrelse skal du overveje følgende:

-Klassestørrelse, bredde eller bredde: er forskellen mellem den højeste værdi i klassen og den laveste.

Klassens størrelse bestemmes ved at dividere rang R med antallet af klasser, der skal overvejes. Området er forskellen mellem den maksimale værdi af dataene og den mindste, som denne:

Klassestørrelse = Rang / antal klasser.

-Klassegrænse: interval fra den nedre grænse til den øvre grænse for klassen.

-Klassemærke: er midtpunktet for intervallet, der betragtes som repræsentativt for klassen. Det beregnes med halvsummen af ​​den øvre grænse og den nedre grænse for klassen.

-Antal klasser: Sturges formel kan bruges:

Antal klasser = 1 + 3.322 log N

Hvor N er antallet af klasser. Da det normalt er et decimaltal, afrundes det til det næste heltal.

Eksempel

En maskine på en stor fabrik er ude af drift på grund af tilbagevendende fejl. De på hinanden følgende perioder med inaktivitet i minutter af maskinen er registreret nedenfor med i alt 100 data:

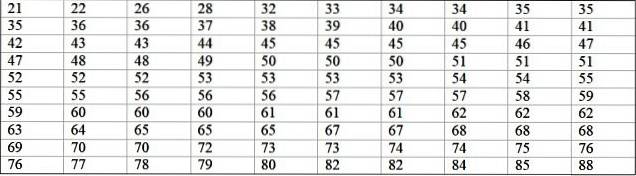
Først bestemmes antallet af klasser:

Antal klasser = 1 + 3.322 log N = 1 + 3.32 log 100 = 7.64 ≈ 8

Klassestørrelse = Område / Antal klasser = (88-21) / 8 = 8.375

Det er også et decimaltal, så 9 tages som klassestørrelse.

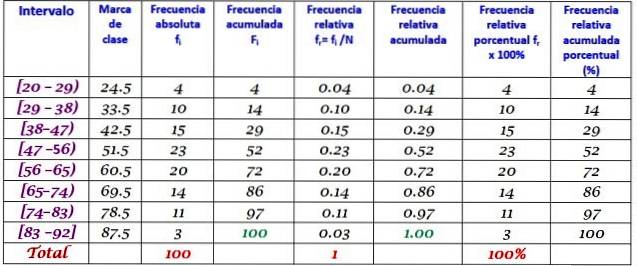
Klassemærket er gennemsnittet mellem klassens øvre og nedre grænse, for eksempel for klasse [20-29] er der et mærke på:

Klassemærke = (29 + 20) / 2 = 24,5

Vi fortsætter på samme måde for at finde klassemarkeringerne for de resterende intervaller.

Træning løst

40 unge indikerede, at tiden i minutter, de brugte på internettet sidste søndag, var følgende, bestilt i stigende rækkefølge:

0; 12; tyve; 35; 35; 38; 40; Fire. Fem; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Det bliver bedt om at konstruere frekvensfordelingen af ​​disse data.

Opløsning

Området R for sættet med N = 40 data er:

R = 220 - 0 = 220

Anvendelse af Sturges-formlen for at bestemme antallet af klasser giver følgende resultat:

Antal klasser = 1 + 3.322 log N = 1 + 3.32 log 40 = 6.3

Da det er et decimal, er det øjeblikkelige heltal 7, derfor er dataene grupperet i 7 klasser. Hver klasse har en bredde på:

Klassestørrelse = Rang / Antal klasser = 220/7 = 31.4

En tæt og rund værdi er 35, og derfor vælges en klassebredde på 35.

Klassemærker beregnes ved at gennemsnitliggøre de øvre og nedre grænser for hvert interval, for eksempel for intervallet [0,35):

Klassemærke = (0 + 35) / 2 = 17,5

Fortsæt på samme måde med de andre klasser.

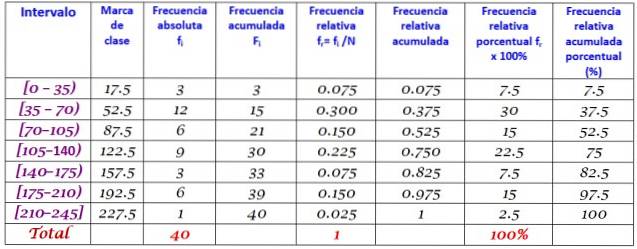
Endelig beregnes frekvenserne efter fremgangsmåden beskrevet ovenfor, hvilket resulterer i følgende fordeling:

Referencer

1. Berenson, M. 1985. Statistik for ledelse og økonomi. Interamericana S.A.
2. Devore, J. 2012. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. 8. plads Udgave. Cengage.
3. Levin, R. 1988. Statistik for administratorer. 2. plads Udgave. Prentice hall.
4. Spiegel, M. 2009. Statistik. Schaum-serien. 4. plads Udgave. Mcgraw bakke.
5. Walpole, R. 2007. Sandsynlighed og statistik for ingeniørvidenskab og videnskab. Pearson.