
Formler for centrifugalkraft, hvordan man beregner det, eksempler, øvelser
Det centrifugal kraft det har tendens til at skubbe drejelige kroppe ud omkring en kurve. Det betragtes som en fiktiv kraft, pseudoforce eller inerti-kraft, fordi det ikke er forårsaget af interaktioner mellem virkelige objekter, men er en manifestation af inerti af ligene. Inerti er den egenskab, der får genstande til at bevare deres hviletilstand eller ensartet retlinjet bevægelse, hvis de har en..
Udtrykket "centrifugalkraft" blev opfundet af videnskabsmanden Christian Huygens (1629-1695). Han sagde, at den krumlinjære bevægelse af planeterne ville have en tendens til at flytte dem væk, medmindre solen udøvede en vis kraft for at holde dem tilbage, og han beregnede, at denne kraft var proportional med kvadratet af hastigheden og omvendt proportional med radius af den beskrevne omkreds..

For dem, der rejser i bil, er centrifugalkraft slet ikke fiktiv. Passagerer i en bil, der drejer til højre, føles skubbet til venstre, og omvendt, når bilen drejer til venstre, oplever folk en kraft til højre, som synes at ønske at flytte dem væk fra centrum af kurven.
Størrelsen af centrifugalkraften Fg beregnes ved hjælp af følgende udtryk:
-Fg er størrelsen af centrifugalkraften
-m er genstandens masse
-v er hastigheden
-R er radius af den buede sti.
Kraft er en vektor, derfor bruges fed skrift til at skelne den fra dens størrelse, som er en skalar.
Det skal du altid huske på Fg vises kun, når bevægelse er beskrevet ved hjælp af en accelereret referenceramme.
I det eksempel, der blev beskrevet i starten, udgør den roterende bil en accelereret reference, da den kræver centripetal acceleration, så jeg kan vende rundt.
Artikelindeks
- 1 Hvordan beregner man centrifugalkraften?
- 1.1 Diagram over frit legeme i et inertialt og ikke-inertialt system
- 2 Eksempler
- 3 Øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 applikationer
- 4.1 Centrifuger
- 4.2 Skiver
- 4.3 Kan ikke kurver
- 5 Referencer
Hvordan beregner man centrifugalkraften?
Valget af referencesystem er afgørende for forståelsen af bevægelsen. En accelereret referenceramme er også kendt som en ikke-inertial ramme..
I denne type system, som en snurrende bil, optræder fiktive kræfter som centrifugalkraft, hvis oprindelse ikke er en reel interaktion mellem objekter. En passager kan ikke sige, hvad der skubber ham ud af kurven, han kan kun bekræfte, at dette er tilfældet.
På den anden side forekommer interaktionerne i et inertialreferencesystem mellem virkelige objekter, såsom kroppen i bevægelse og Jorden, som giver vægt, eller mellem kroppen og overfladen, som den bevæger sig på, som har friktion og normal.
En observatør, der står ved siden af vejen og ser, hvordan bilen drejer kurven, er et godt eksempel på et inertialreferencesystem. For denne observatør drejer bilen, fordi en kraft rettet mod centrum af kurven virker på den, hvilket tvinger den til ikke at forlade den. Det handler om centripetal kraft produceret af friktion mellem dækkene og fortovet.
I en inerti-referenceramme vises ikke centrifugalkraften. Derfor er det første trin til at beregne det nøje at vælge det referencesystem, der skal bruges til at beskrive bevægelsen..
Endelig skal det bemærkes, at inertialreferencesystemerne ikke nødvendigvis behøver at være i ro, ligesom observatøren, der ser køretøjet dreje kurven. En inerti-referenceramme, kendt som laboratorieramme, det kan også være på farten. Selvfølgelig med konstant hastighed i forhold til en inerti.
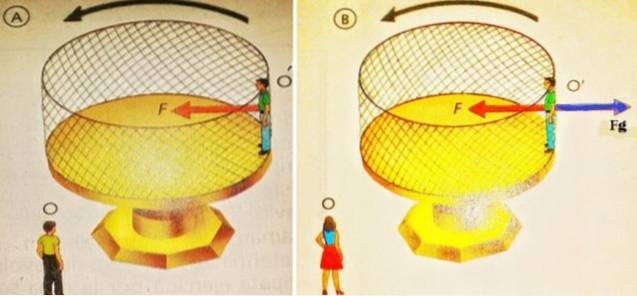
Frikroppsdiagram i et inertialt og ikke-inertialt system
I den næste figur til venstre står en observatør O og ser på O ', som er på platformen, der roterer i den angivne retning. For O, som er en inertial ramme, fortsætter O 'bestemt med at rotere på grund af den centripetale kraft Fc produceret af gittervæggen på bagsiden af O '.

Kun i inertiale referencerammer er det gyldigt at anvende Newtons anden lov, der siger, at nettokraften er lig med masseproduktet og accelerationen. Og ved at gøre det, med det viste frie kropsdiagram, får vi:
Fc = mac
Fc= mvto / R
På samme måde er der i figuren til højre også et fritlegemsdiagram, der beskriver, hvad observatøren O 'ser. Fra hans synspunkt er han i ro, derfor styrker kræfterne på ham.
Disse kræfter er: de normale F, at væggen udøver på den i rødt og rettet mod centrum og centrifugalkraften Fg der skubber det udad, og som ikke er udsprunget af nogen interaktion, er en ikke-inertial kraft, der vises i de roterende referencerammer.
Centrifugalkraften er fiktiv, den afbalanceres af en reel kraft, kontakten eller den normale kraft, der peger mod centrum. Derfor:
∑Fx = 0 → Fg - F = 0
Fg = F
Eksempler
Selvom centrifugalkraft betragtes som en pseudokraft, er dens virkninger ret virkelige, som det kan ses i følgende eksempler:
- I ethvert spindende spil i en forlystelsespark er centrifugalkraft til stede. Hun sørger for, at vi "løber væk fra centrum" og tilbyder konstant modstand, hvis du prøver at gå ind i midten af en bevægelig karrusel. I det følgende pendul kan du se centrifugalkraften:
- Coriolis-effekten stammer fra Jordens rotation, hvilket får Jorden til at stoppe med at være en inerti-ramme. Derefter vises Coriolis-kraften, som er en pseudokraft, der afbøjer genstande lateralt, ligesom folk forsøger at gå på en pladespiller..
Uddannelse
Øvelse 1
En bil, der snurrer med acceleration TIL til højre er et udstoppet legetøj hængende fra det indvendige bakspejl. Tegn og sammenlign frit legemsdiagrammer for legetøjet set fra:
a) Tragtreferencerammen for en observatør, der står på vejen.
b) En passager, der rejser i bilen.
Løsning til
En observatør, der står på vejen, bemærker, at legetøjet bevæger sig hurtigt med acceleration TIL til højre.
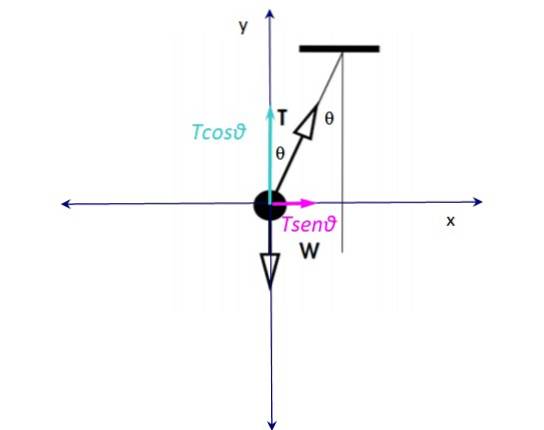
Der er to kræfter, der virker på legetøjet: på den ene side spændingen i strengen T og lodret vægt ned W. Vægten afbalanceres med den lodrette spændingskomponent Tcosθ, Dermed:
W - Tcosθ = 0
Den vandrette komponent af stress: T. senθ er den ubalancerede kraft, der er ansvarlig for accelerationen til højre, derfor er den centripetale kraft:
Fc= T. sinθ = mac
Løsning b
For en passager i bilen hænger legetøjet i ligevægt, og diagrammet er som følger:

Som i det foregående tilfælde kompenseres vægten og den lodrette komponent af spændingen. Men den vandrette komponent afbalanceres af den fiktive kraft Fg = mA, så det:
-mA + Tsenθ = 0
Fg = mA
Øvelse 2
En mønt er på kanten af en gammel vinylpladespiller, hvis radius er 15 cm og roterer med en hastighed på 33 omdrejninger / minut. Find den mindste statiske friktionskoefficient, der er nødvendig for, at mønten kan forblive på plads, ved hjælp af referencerammen solidaritet med mønten.
Opløsning
På figuren er diagrammet for frit legeme for en observatør, der bevæger sig med mønten. Det normale N at pladespilleren udøver lodret op, er afbalanceret med vægten W, mens centrifugalkraften Fg kompenseres af statisk friktion Frøre ved.
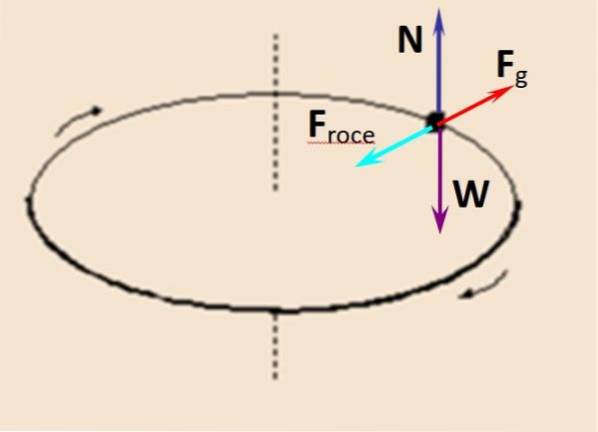
N - W = 0
Frøre ved - Fg = 0
Størrelsen af centrifugalkraften er mvto/ R, som sagt i starten, så:
Frøre ved = Fg = mvto/ R
På den anden side er den statiske friktionskraft givet af:
Fgnid = μs.N
Hvor μs er koefficienten for statisk friktion, en dimensionsløs størrelse, hvis værdi afhænger af, hvordan overfladerne er i kontakt. Udskiftning af denne ligning er:
μs.N = mvto/ R → μs = mvto/R.N
Det er stadig at bestemme størrelsen af det normale, der er relateret til vægten i henhold til N = mg. Udskifter igen:
μs = mvto/R.mg → μs = vto/ Rg
Tilbage til udsagnet rapporterer det, at mønten roterer med en hastighed på 33 omdrejninger / minut, hvilket er vinkelhastigheden eller vinkelfrekvensen ω, relateret til lineær hastighed v:
v = ω.R = 33 omdrejninger / min. 2π radianer / omdrejningstal 15 cm. (1 min / 60 s) = 51,8 cm / s
μs = vto/Rg=( 51,8 cm / s)to/ (15 cm x 981 cm / sto) = 0,18
Resultaterne af denne øvelse ville have været de samme, hvis der var valgt en inerti-referenceramme. I dette tilfælde er den eneste kraft, der er i stand til at forårsage acceleration mod centrum, statisk friktion..
Ansøgninger
Som vi har sagt, er centrifugalkraften en fiktiv kraft, der ikke vises i inerti-rammer, som er de eneste, hvor Newtons love er gyldige. I dem er den centripetale kraft ansvarlig for at give kroppen den nødvendige acceleration mod centrum.
Den centripetale kraft er ikke en anden kraft end dem, der allerede er kendt. Tværtimod er det netop disse, der spiller rollen som centripetale kræfter, når det er relevant. For eksempel tyngdekraften, der får Månen til at kredser rundt om Jorden, spændingen i et reb, som en sten roteres med, den statiske friktion og den elektrostatiske kraft.
Da accelererede referencerammer findes i praksis, har fiktive kræfter imidlertid meget reelle effekter. For eksempel er her tre vigtige applikationer, hvor de har konkrete effekter:
Centrifuger
Centrifuger er instrumenter, der er meget anvendte i laboratoriet. Ideen er at få en blanding af stoffer til at rotere ved høj hastighed, og disse stoffer med større masse oplever en større centrifugalkraft, ifølge ligningen beskrevet i starten..
Derefter vil de mest massive partikler have tendens til at bevæge sig væk fra rotationsaksen og således adskilles fra de lettere, som vil forblive tættere på centrum..
Vaskemaskine
Automatiske vaskemaskiner har forskellige centrifugeringscyklusser. I dem centrifugeres tøjet for at fjerne det resterende vand. Jo flere omdrejninger cyklussen er, desto mindre fugtig bliver tøjet i slutningen af vasken.

Kan ikke kurver
Biler er bedre til at svinge på veje, fordi sporet skråner lidt mod centrum af kurven, som er kendt som superelevation. På denne måde afhænger bilen ikke udelukkende af den statiske friktion mellem dækkene og vejen for at fuldføre svinget uden at forlade kurven..
Referencer
- Acosta, Victor. Konstruktion af en didaktisk vejledning om centrifugalkraft for studerende i cyklus V klasse 10. Hentet fra: bdigital.unal.edu.co.
- Toppr. Lov om bevægelse: Cirkulær bevægelse. Gendannet fra: toppr.com.
- Resnick, R. (1999). Fysisk. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
- Autonome universitet i staten Hidalgo. Centrifugal kraft. Gendannet fra: uaeh.edu.mx
- Wikipedia. Centrifuger. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer