EN surjective funktion er ethvert forhold, hvor hvert element, der hører til kodomænet, er et billede af mindst et element af domænet. Også kendt som funktion på, er en del af klassificeringen af funktioner med hensyn til den måde, deres elementer er relateret på.
For eksempel en funktion F: A → B defineret af F (x) = 2x
Hvilket lyder "F hvad med TIL så længe B defineret af F (x) = 2x "
Det er på tide at definere start- og finish-sæt A og B.
A: 1, 2, 3, 4, 5 Nu skal de værdier eller billeder, som hvert af disse elementer viser, når de evalueres i F, vil være elementerne i codomain.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Således danner helheden B: 2, 4, 6, 8, 10
Det kan derefter konkluderes, at:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 defineret af F (x) = 2x Det er en overvejelsesfunktion
Hvert element i kodomænet skal være resultatet af mindst en operation af den uafhængige variabel gennem den pågældende funktion. Der er ingen begrænsning af billeder, et element i codomain kan være et billede af mere end et element af domænet og stadig prøve et surjective funktion.
Billedet viser 2 eksempler med surjective funktioner.
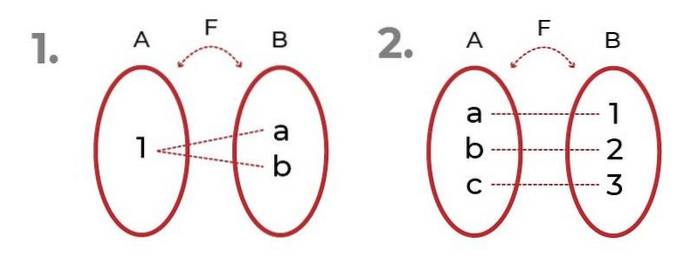
I den første bemærkes det, at billederne kan henvises til det samme element uden at gå på kompromis med surjectivity af funktionen.
I det andet ser vi en retfærdig fordeling mellem domæne og billeder. Dette giver anledning til bijektiv funktion, hvor kriterierne i injektionsfunktion og surjektiv funktion.
En anden metode til at identificere surjective funktioner, er at kontrollere, om codomainen er lig med funktionsområdet. Dette betyder, at hvis ankomstsættet er lig med de billeder, der leveres af funktionen, når man vurderer den uafhængige variabel, funktionen er overvejende.
Artikelindeks
At overveje overvejelse til en funktion skal følgende være opfyldt:
Være F: DF → CF
∀ b ℮ CF OG til ℮ DF / F (a) = b
Dette er den algebraiske måde at fastslå det på for alle "b", der hører til CF der er et “a”, der tilhører DF således at funktionen F, der evalueres i "a", er lig med "b".
Surjectivity er en egenskab ved funktioner, hvor codomain og området er ens. Således udgør elementerne, der evalueres i funktionen, ankomstsættet.
Nogle gange en funktion, der ikke er overvejelse, det kan underkastes visse betingelser. Disse nye forhold kan gøre det til et surjective funktion.
Alle former for ændringer af funktionens domæne og codomain er gyldige, hvor målet er at opfylde surjektivitetsegenskaberne i den tilsvarende relation.
For at opfylde betingelserne i surjectivity forskellige konditioneringsteknikker skal anvendes, dette for at sikre, at hvert element i kodomænet er inden for sæt af billeder af funktionen.
A: [Alle reelle tal]
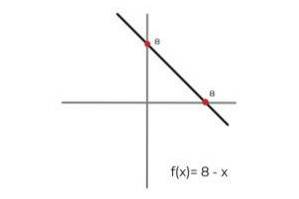
I dette tilfælde beskriver funktionen en kontinuerlig linje, der dækker alle reelle tal i både dens domæne og rækkevidde. Fordi rækkevidden af funktionen RF svarer til codomain R Det kan konkluderes, at:
F: R → R defineret af linjen F (x) = 8 - x er en surjective funktion.
Dette gælder for alle lineære funktioner (Funktioner hvis største grad af variablen er en).
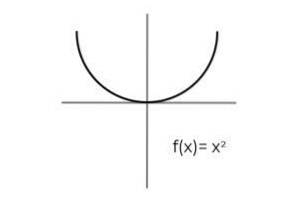
Den første ting at overveje er codomain af F, som består af de reelle tal R. Der er ingen måde for funktionen at returnere negative værdier, hvilket udelukker de virkelige negativer fra de mulige billeder.
Konditionering af codomain til intervallet [0 , ∞ ]. Det undgås at lade elementerne i codomain være uafhængige F.
Billederne gentages for par af elementer i den uafhængige variabel, såsom x = 1 Y x = - 1. Men dette påvirker kun injektionsevne af funktionen, ikke er et problem for denne undersøgelse.
På denne måde kan det konkluderes, at:
F: R →[0, ∞ ) defineret af F (x) = xto Det er en overvejende funktion
F: R → R defineret af F (x) = Sen (x)
F: R → R defineret af F (x) = Cos (x)
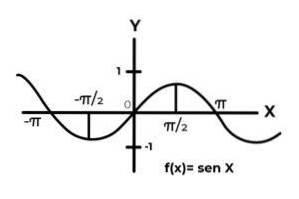
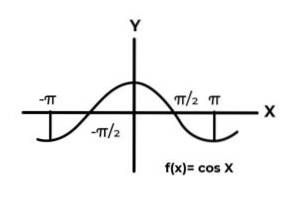
Opførelsen af de trigonometriske funktioner svarer til bølgerne, og det er meget almindeligt at finde gentagelser af den afhængige variabel mellem billederne. Også i de fleste tilfælde er funktionsområdet begrænset til en eller flere sektorer i den virkelige linje.
Dette er tilfældet med Sine- og Cosine-funktionerne. Hvor deres værdier svinger i intervallet [-1, 1]. Dette interval skal betinges af codomain for at opnå funktionens overslagskraft.
F: R →[ -elleve ] defineret af F (x) = Sen (x) Det er en overvejende funktion
F: R →[ -elleve ]defineret af F (x) = Cos (x) Det er en form for funktion
F: [0, ∞ ) → R defineret af F (x) = ± √x angive, om det er en surjective funktion
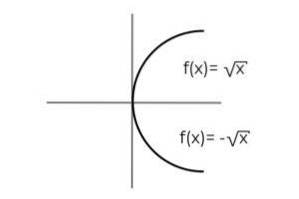
Funktionen F (x) = ± √x Det har det særlige, at det definerer 2 afhængige variabler til hver værdi af "x". Det vil sige, at området modtager 2 elementer for hver, der er lavet i domænet. En positiv og negativ værdi skal verificeres for hver værdi af "x".
Når man observerer startsættet, bemærkes det, at domænet allerede er blevet begrænset, dette for at undgå de ubestemtheder, der produceres, når man vurderer et negativt tal inden for en jævn rod.
Når man verificerer funktionsområdet, bemærkes det, at hver værdi i kodomænet hører til området.
På denne måde kan det konkluderes, at:
F: [0, ∞ ) → R defineret af F (x) = ± √x Det er en overvejende funktion
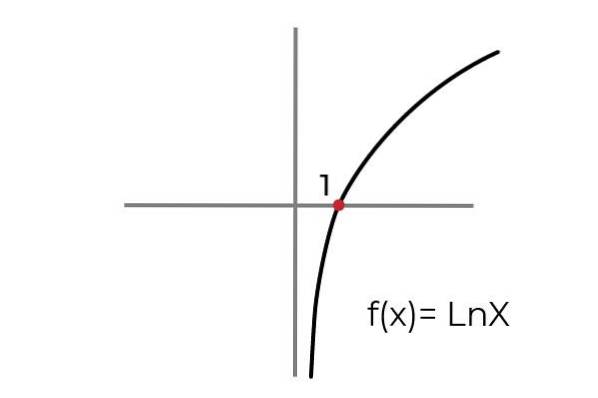
Som vist i grafen funktionen F (x) = Ln xdet er defineret for værdier på "x" større end nul. Mens værdierne for "og" eller billederne kan have en hvilken som helst reel værdi.
På denne måde kan vi begrænse domænet for F (x) = til interval (0 , ∞ )
Så længe rækkevidden for funktionen kan holdes som et sæt reelle tal R.
I betragtning af dette kan det konkluderes, at:
F: [0, ∞ ) → R defineret af F (x) = Ln x Det er en form for funktion
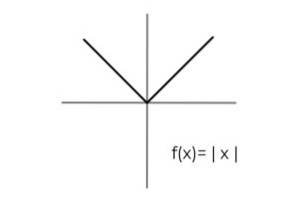
Funktionens domæne gælder for alle reelle tal R. På denne måde skal den eneste konditionering udføres i codomain under hensyntagen til, at den absolutte værdifunktion kun tager positive værdier..
Vi fortsætter med at etablere codomain for funktionen, der svarer til den samme rang
[0 , ∞ )
Nu kan det konkluderes, at:
F: [0, ∞ ) → R defineret af F (x) = | x | Det er en form for funktion
Endnu ingen kommentarer