
Omvendt trigonometriske funktioner værdi, derivater, eksempler, øvelser
Det inverse trigonometriske funktioner, Som navnet antyder, er de de tilsvarende inverse funktioner af sinus-, cosinus-, tangent-, cotangent-, secant- og cosecant-funktioner..
Inverse trigonometriske funktioner er betegnet med samme navn som deres tilsvarende direkte trigonometriske funktion plus præfikset bue. Dermed:
1.- arcsen (x) er funktionens inverse trigonometriske funktion sen (x)
to.- arccos (x) er funktionens inverse trigonometriske funktion cos (x)
3.- arctan (x) er funktionens inverse trigonometriske funktion så (x)
4.- arccot (x) er funktionens inverse trigonometriske funktion barneseng (x)
5.- buesek (x) er funktionens inverse trigonometriske funktion sek (x)
6.- arccsc (x) er funktionens inverse trigonometriske funktion csc (x)
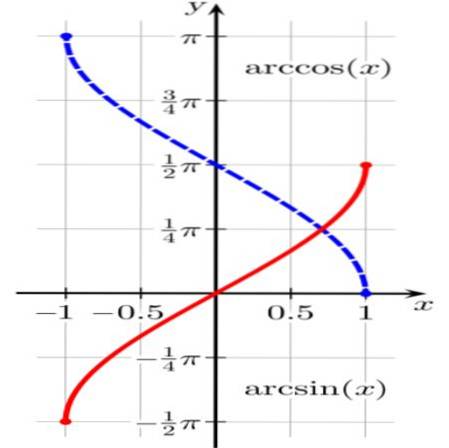
Funktionen θ = lysbue (x) resulterer i en enhedsbue θ (eller vinkel i radianer θ) sådan at sin (θ) = x.
Således er f.eks. Bue (√3 / 2) = π / 3, da som bekendt sinus af π / 3 radianer er lig med √3 / 2.
Artikelindeks
- 1 Hovedværdi af inverse trigonometriske funktioner
- 1.1 Tabel over domæner og intervaller for inverse trigonometriske funktioner
- 2 Afledte af inverse trigonometriske funktioner
- 3 eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 4 Øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 4.3 - Øvelse 3
- 5 Referencer
Hovedværdi af inverse trigonometriske funktioner
For at en matematisk funktion har f (x) en invers g (x) = f-1(x) det er nødvendigt, at denne funktion er injektionsmiddel, hvilket betyder, at hver værdi y af ankomstsættet for funktionen f (x) kommer fra en og kun en værdi x.
Det er klart, at dette krav ikke er opfyldt af nogen trigonometrisk funktion. For at afklare punktet skal du bemærke, at værdien y = 0,5 kan opnås fra sinusfunktionen på følgende måder:
- sin (π / 6) = 0,5
- sin (5π / 6) = 0,5
- sin (7π / 6) = 0,5
Og mange flere, da sinusfunktionen er periodisk med periode 2π.
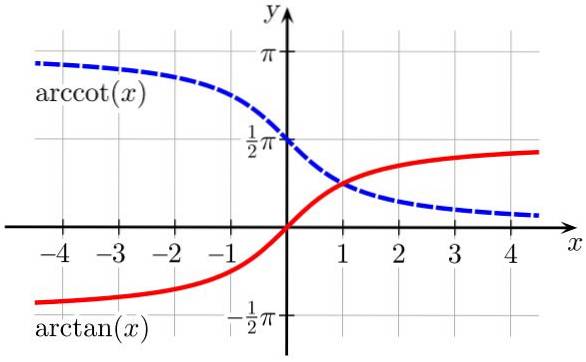
For at definere de inverse trigonometriske funktioner er det nødvendigt at begrænse domænet for deres tilsvarende direkte trigonometriske funktioner, således at de opfylder injektivitetskravet.
Det begrænsede domæne af den direkte funktion vil være området eller hovedgrenen for dens tilsvarende inverse funktion.
Tabel over domæner og intervaller for inverse trigonometriske funktioner

Afledte af inverse trigonometriske funktioner
For at opnå derivaterne af de inverse trigonometriske funktioner anvendes derivaternes egenskaber, især derivatet af en invers funktion.
Hvis vi betegner med f (y) funktionen og med f-1(x) til dens inverse funktion, så er afledningen af den inverse funktion relateret til afledningen af den direkte funktion ved følgende forhold:
[F-1(x)] '= 1 / f' [f-1(x)]
For eksempel: hvis x = f (y) = √y er den direkte funktion, vil dens inverse være
y = f-1(x) = xto. Lad os anvende reglen om det afledte af det inverse i dette enkle tilfælde for at se, at denne regel faktisk er opfyldt:
[xto] '= 1 / [√y]' = 1 / (½ y-½ = 2 og½ = 2 (xto)½ = 2x
Nå, vi kan bruge dette trick til at finde derivaterne af de inverse trigonometriske funktioner.
For eksempel tager vi θ = lysbue (x) som den direkte funktion, så vil dens inverse funktion være sin (θ) = x.
[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sin (θ)to) = ...
… = 1 / √ (1 - xto) .
På denne måde kan alle derivater af de inverse trigonometriske funktioner opnås, som er vist nedenfor:

Disse derivater er gyldige for ethvert argument z, der hører til de komplekse tal, og derfor er de også gyldige for ethvert reelt argument x, da z = x + 0i.
Eksempler
- Eksempel 1
Find arctan (1).
Opløsning
Arctan (1) er enhedens bue (vinkel i radianer) ፀ således at tan (ፀ) = 1. Denne vinkel er ፀ = π / 4 fordi tan (π / 4) = 1. Så arctan (1) = π / 4.
- Eksempel 2
Beregn lysbue (cos (π / 3)).
Opløsning
Vinklen π / 3 radianer er en bemærkelsesværdig vinkel, hvis cosinus er ½, så problemet koges ned til at finde lysbue (½).
Så er det et spørgsmål om at finde, hvilken vinkel hvis sinus giver ½. Denne vinkel er π / 6, da sin (π / 6) = sin (30º) = ½. Derfor er arcsen (cos (π / 3)) = π / 6.
Uddannelse
- Øvelse 1
Find resultatet af følgende udtryk:
sek (arctan (3)) + csc (arccot (4))
Opløsning
Vi starter med at navngive α = arctan (3) og β = arccot (4). Derefter ser udtrykket, som vi skal beregne, sådan ud:
sek (α) + csc (β)
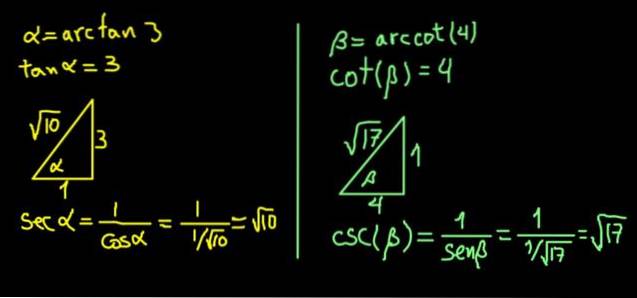
Udtrykket α = arctan (3) svarer til at sige tan (α) = 3.
Da tangenten er det modsatte ben over den tilstødende, konstruerer vi en højre trekant med benet modsat α på 3 enheder og et tilstødende ben på 1 enhed, så tan (α) = 3/1 = 3.
I en ret trekant bestemmes hypotenusen af Pythagoras sætning. Med disse værdier er resultatet √10, så:
sek (α) = hypotenus / tilstødende ben = √10 / 1 = √10.
Tilsvarende svarer β = arccot (4) til at bekræfte, at barneseng (β) = 4.
Vi konstruerer en trekant med højre ben ved siden af β på 4 enheder og et modsat ben på 1 enhed, så barneseng (β) = 4/1.
Trekanten afsluttes straks ved at finde sin hypotenus takket være Pythagoras sætning. I dette tilfælde viste det sig at have √17 enheder. Derefter beregnes csc (β) = hypotenuse / modsat ben = √17 / 1 = √17.
Husk at det udtryk, vi skal beregne, er:
sek (arctan (3)) + csc (arccot (4)) = sec (α) + csc (β) =…
… = √10 + √17 = 3,16 + 4,12 = 7,28.
- Øvelse 2
Find løsningerne til:
Cos (2x) = 1 - Sen (x)

Opløsning
Det er nødvendigt, at alle trigonometriske funktioner udtrykkes i samme argument eller vinkel. Vi bruger identiteten af den dobbelte vinkel:
Cos (2x) = 1-2 Sento(x)
Derefter reduceres det originale udtryk til:
1 - 2 Sento(x) = 1 - Sen x
Når det er forenklet og indregnet, udtrykkes det som:
sin (x) (2 sin (x) - 1) = 0
Hvilket giver anledning til to mulige ligninger: Sen (x) = 0 med opløsning x = 0 og en anden ligning sin (x) = ½ med x = π / 6 som opløsning.
Løsningerne til ligningen er: x = 0 eller x = π / 6.
- Øvelse 3
Find løsningerne i følgende trigonometriske ligning:
cos (x) = syndto(x)
Opløsning
For at løse denne ligning er det praktisk at kun placere en type trigonometrisk funktion, så vi bruger den grundlæggende trigonometriske identitet, så den oprindelige ligning omskrives som følger:
cos (x) = 1 - costo(x)
Hvis vi navngiver y = cos (x), kan udtrykket omskrives som:
Yto + og - 1 = 0
Det er en ligning af anden grad i y, hvis løsninger er:
y = (-1 ± √5) / 2
Derefter er værdierne af x, der tilfredsstiller den oprindelige ligning:
x = arccos ((-1 ± √5) / 2)
Den virkelige løsning er den med et positivt tegn x = 0,9046 rad = 51,83º.
Den anden løsning er kompleks: x = (π - 1.06 i) rad.
Referencer
- Hazewinkel, M. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publishers / Springer Science & Business Media.
- Mate Mobile. Inverse trigonometriske funktioner. Gendannet fra: matemovil.com
- Universformler. Inverse trigonometriske funktioner. Gendannet fra: universoformulas.com
- Weisstein, Eric W. Inverse trigonometriske funktioner. Gendannet fra: mathworld.wolfram.com
- Wikipedia. Inverse trigonometriske funktioner. Gendannet fra: en.wikipedia.com


Endnu ingen kommentarer