
Euklidisk geometrihistorie, grundlæggende begreber og eksempler

Det euklidisk geometri svarer til undersøgelsen af egenskaberne ved geometriske rum, hvor Euklids aksiomer er opfyldt. Selvom dette udtryk undertiden bruges til at dække geometrier, der har højere dimensioner med lignende egenskaber, er det generelt synonymt med klassisk geometri eller plangeometri..
I det 3. århundrede a. C. Euclid og hans disciple skrev Elementer, et værk, der omfattede den tids matematiske viden udstyret med en logisk-deduktiv struktur. Siden da blev geometri en videnskab, oprindeligt for at løse klassiske problemer og udviklede sig til at være en formativ videnskab, der hjælper med at ræsonnere..

Artikelindeks
- 1 Historie
- 2 grundlæggende
- 2.1 Almindelige forestillinger
- 2.2 Postulater eller aksiomer
- 3 eksempler
- 3.1 Første eksempel
- 3.2 Andet eksempel
- 3.3 Tredje eksempel
- 4 Referencer
Historie
For at tale om historien om euklidisk geometri er det vigtigt at starte med Euklid af Alexandria og Elementer.
Da Egypten blev efterladt i hænderne på Ptolemaios I, efter Alexander den Store død, begyndte han sit projekt på en skole i Alexandria.
Blandt de vismænd, der underviste på skolen, var Euclid. Det spekuleres i, at hans fødsel stammer fra cirka 325 f.Kr. C. og hans død af 265 a. C. Vi kan med sikkerhed vide, at han gik på Platons skole.
I mere end tredive år underviste Euclid i Alexandria og byggede sine berømte elementer: han begyndte at skrive en udtømmende beskrivelse af sin tids matematik. Euklids lære gav fremragende disciple, såsom Archimedes og Apollonius af Perga.
Euclid blev anklaget for at strukturere de gamle opdagelser fra de gamle grækere i Elementer, men i modsætning til sine forgængere begrænser den sig ikke til at bekræfte, at en sætning er sand; Euclid tilbyder en demonstration.
Det Elementer de er et kompendium med tretten bøger. Efter Bibelen er det den mest udgivne bog med mere end tusind udgaver.
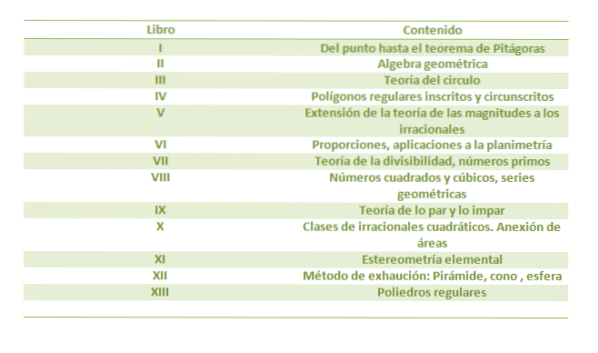
Det Elementer er Euclids mesterværk inden for geometri og tilbyder en endelig behandling af geometrien i to dimensioner (planet) og tre dimensioner (rum), dette er oprindelsen til det, vi nu kender som euklidisk geometri.
Basale koncepter
Elementerne består af definitioner, almindelige forestillinger og postulater (eller aksiomer) efterfulgt af sætninger, konstruktioner og bevis..
- Et punkt er det, der ikke har nogen dele.
- En linje er en længde, der ikke har nogen bredde.
- En lige linje er en, der ligger lige i forhold til de punkter, der er i dette.
- Hvis to linjer skæres, så de tilstødende vinkler er ens, kaldes vinklerne retvinkler, og linjerne kaldes vinkelret.
- Parallelle linjer er dem, der, når de befinder sig i samme plan, aldrig krydser hinanden.
Efter disse og andre definitioner præsenterer Euclid os en liste med fem postulater og fem forestillinger..
Almindelige forestillinger
- To ting, der er lig med en tredjedel, er lig med hinanden.
- Hvis de samme ting føjes til de samme ting, er resultaterne de samme.
- Hvis lige ting trækkes fra lige ting, er resultaterne ens.
- Ting, der matcher hinanden, er lig med hinanden.
- Det samlede antal er større end en del.
Postulater eller aksiomer
- Én og kun en linje passerer gennem to forskellige punkter.
- Lige linjer kan forlænges på ubestemt tid.
- En cirkel kan tegnes med ethvert centrum og enhver radius.
- Alle rette vinkler er ens.
- Hvis en lige linje krydser to lige linjer, så de indvendige vinkler på den samme side udgør mindre end to rette vinkler, så krydser de to linjer på den side..
Dette sidste postulat er kendt som det parallelle postulat, og det blev omformuleret som følger: "For et punkt uden for en linje kan der tegnes en parallel til den givne linje".
Eksempler
Her er nogle sætninger om Elementer de tjener til at vise egenskaber ved geometriske rum, hvor de fem postulater af Euclid er opfyldt; Derudover vil de illustrere den logisk-deduktive begrundelse, som denne matematiker brugte.
Første eksempel
Forslag 1.4. (LAL)
Hvis to trekanter har to sider, og vinklen mellem dem er ens, så er de andre sider og de andre vinkler ens..
Demonstration
Lad ABC og A'B'C 'være to trekanter med AB = A'B', AC = A'C 'og vinklerne BAC og B'A'C' ens. Lad os flytte trekanten A'B'C ', så A'B' falder sammen med AB og den vinkel B'A'C 'falder sammen med vinklen BAC.
Så linje A'C 'falder sammen med linje AC, således at C' falder sammen med C. Derefter skal post BC ved postulat 1 falde sammen med linje B'C '. Derfor falder de to trekanter sammen, og derfor er deres vinkler og sider ens.
Andet eksempel
Proposition 1.5. (Pons Asinorum)
Hvis en trekant har to lige store sider, så er de modsatte vinkler til disse sider ens..
Demonstration
Antag, at trekanten ABC har lige sider AB og AC.
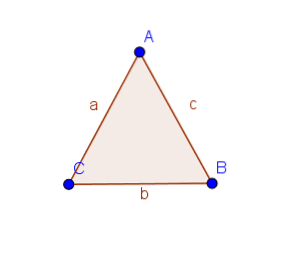
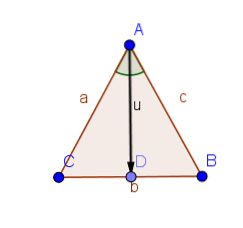
Så trekanterne ABD og ACD har to lige store sider, og vinklerne mellem dem er ens. Således er vinklerne ABD og ACD ved Proposition 1.4 ens.
Tredje eksempel
Proposition 1.31
Du kan konstruere en linje parallelt med en linje givet af et givet punkt.
Bygning
Givet en linje L og et punkt P, trækkes en linje M gennem P og skærer L. Derefter tegnes en linje N gennem P, der skærer L. Nu trækkes en linje N gennem P, der skærer M og danner en vinkel lig med den, som L danner med M.

Bekræftelse
N er parallel med L.
Demonstration
Antag, at L og N ikke er parallelle og skærer hinanden ved et punkt A. Lad B være et punkt i L ud over A. Overvej linjen O, der passerer gennem B og P. Derefter skærer O M i vinkler, der tilsammen er mindre end to lige.
Så med 1,5 skal linjen O krydse linjen L på den anden side af M, så L og O krydser hinanden ved to punkter, hvilket modsiger Postulat 1. Derfor skal L og N være parallelle.
Referencer
- Euklidiske elementer af geometri. National Autonomous University of Mexico
- Euclid. De første seks bøger og den ellevte og tolvte af Euclids elementer
- Eugenio Filloy Yague. Didaktik og historie med euklidisk geometri, Grupo Editorial Iberoamericano
- K. Ribnikov. Matematikhistorie. Mir Editorial
- Viloria, N., & Leal, J. (2005) Plane Analytical Geometry. Redaktionelt Venezolana C.A.


Endnu ingen kommentarer