
Pythagoras identitets demonstration, eksempel, øvelser
De er Pythagoras identiteter alle trigonometriske ligninger, der holder en hvilken som helst værdi af vinklen, og er baseret på den pythagoriske sætning. Den mest berømte af Pythagoras identiteter er den grundlæggende trigonometriske identitet:
Sento(α) + Costo(α) = 1
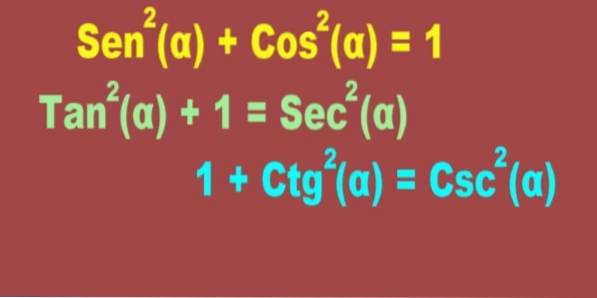
Næste i betydning, og jeg bruger den tangentlige og sekantes pythagoreanske identitet:
Såto(α) + 1 = sekto(α)
Og den Pythagoras trigonometriske identitet, der involverer cotangenten og cosecanten:
1 + Ctgto(α) = Cscto(α)
Artikelindeks
- 1 demo
- 1.1 Sinus og cosinus
- 1.2 Den grundlæggende identitet
- 1.3 Tangensaksen
- 1.4 Tangensens pythagoriske identitet
- 2 Eksempel
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referencer
Demonstration
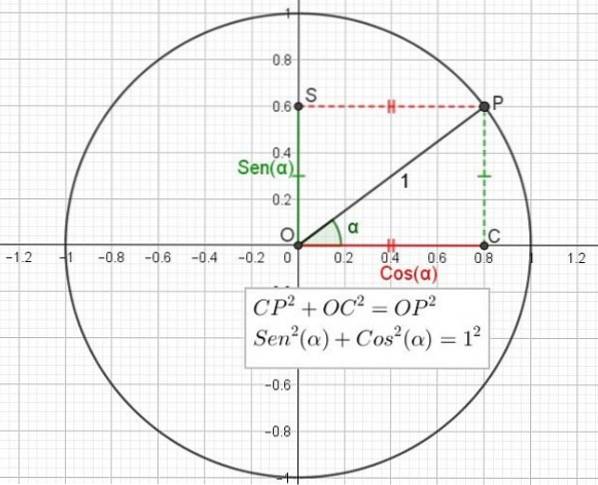
De trigonometriske forhold bryst Y cosinus de er repræsenteret i en cirkel med radius 1 (1) kendt som en trigonometrisk cirkel. Nævnte cirkel har centrum ved oprindelsen af koordinaterne O.
Vinklerne måles fra den positive halvakse af X, for eksempel vinklen α i figur 2 (se nedenfor). Mod uret, hvis vinklen er positiv, og med uret, hvis den er en negativ vinkel.
Strålen med oprindelse O og vinkel α er tegnet, som skærer enhedens cirkel ved punkt P. Punkt P projiceres vinkelret på den vandrette akse X, hvilket giver anledning til punkt C. Tilsvarende projiceres P vinkelret på den lodrette akse Y og giver sted til punkt S.
Vi har den rigtige trekant OCP ved C.
Sinus og cosinus
Det skal huskes, at det trigonometriske forhold bryst er defineret i en højre trekant som følger:
Sinus for en vinkel af trekanten er forholdet eller kvotienten mellem benet modsat vinklen og trekantens hypotenus.
Anvendt på trekanten OCP i figur 2 ville det se sådan ud:
Sen (a) = CP / OP
men CP = OS og OP = 1, således at:
Sen (α) = OS
Dette betyder, at projektion OS på Y-aksen har en værdi lig med sinus for den viste vinkel. Det skal bemærkes, at den maksimale værdi af sinus for en vinkel (+1) opstår, når α = 90º og minimum (-1), når α = -90º eller α = 270º.
Tilsvarende er cosinus for en vinkel kvotienten mellem benet, der støder op til vinklen og trekantens hypotenus..
Anvendt på trekanten OCP i figur 2 ville det se sådan ud:
Cos (a) = OC / OP
men OP = 1, således at:
Cos (a) = OC
Dette betyder, at fremspringet OC på X-aksen har en værdi lig med sinus for den viste vinkel. Det skal bemærkes, at den maksimale værdi af cosinus (+1) opstår, når α = 0º eller α = 360º, mens minimumsværdien af cosinus er (-1), når α = 180º.
Den grundlæggende identitet
For den rigtige trekant OCP i C anvendes den pythagoriske sætning, som siger, at summen af benets firkant er lig med hypotenusens firkant:
CPto + OCto = OPto
Men det er allerede blevet sagt, at CP = OS = Sen (α), at OC = Cos (α) og at OP = 1, så det foregående udtryk kan omskrives som en funktion af sinus og cosinus for vinklen:
Sento(α) + Costo(α) = 1
Tangensens akse
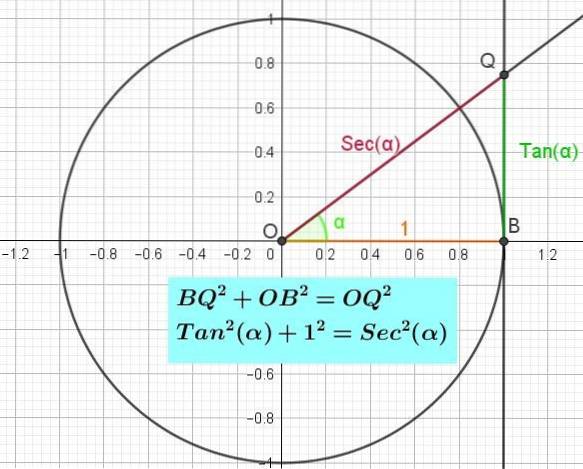
Ligesom X-aksen i den trigonometriske cirkel er cosinusaksen og Y-aksen sinusaksen, er der på samme måde tangentaksen (se figur 3), som netop er tangentlinien til enhedens cirkel ved punkt B af koordinater (1, 0).
Hvis du vil vide værdien af tangentens vinkel, tegner du vinklen fra den positive halvakse af X, krydset mellem vinklen og tangentens akse definerer et punkt Q, længden af segmentet OQ er vinkelens tangens.
Dette skyldes, at vinklen α pr. Definition er det modsatte ben QB mellem det tilstødende ben OB. Det vil sige, Tan (α) = QB / OB = QB / 1 = QB.
Den tangentiske pythagorasiske identitet
Pythagoras identitet af tangenten kan bevises ved at overveje den rigtige trekant OBQ ved B (figur 3). Anvendelse af Pythagoras sætning til denne trekant har vi den BQto + OBto = OQto. Men det er allerede blevet sagt, at BQ = Tan (α), at OB = 1 og at OQ = Sec (α), så at vi erstatter den rigtige trekant OBQ i Pythagoras ligestilling:
Såto(α) + 1 = sekto(α).
Eksempel
Kontroller, om de pythagoriske identiteter er opfyldt i den højre trekant med ben AB = 4 og BC = 3.
Løsning: Benene er kendt, hypotenusen skal bestemmes, hvilket er:
AC = √ (AB ^ 2 + BC ^ 2) = √ (4 ^ 2 + 3 ^ 2) = √ (16 + 9) = √ (25) = 5.
Vinklen ∡BAC kaldes α, ∡BAC = α. Nu bestemmes de trigonometriske forhold:
Sen α = BC / AC = 3/5
Cos α = AB / AC = 4/5
Så α = BC / AB = 3/4
Cotan α = AB / BC = 4/3
Sec α = AC / AB = 5/4
Csc α = AC / BC = 5/3
Det begynder med den grundlæggende trigonometriske identitet:
Sento(α) + Costo(α) = 1
(3/5) ^ 2 + (4/5) ^ 2 = 9/25 + 16/25 = (9 +16) / 25 = 25/25 = 1
Det konkluderes, at det er opfyldt.
- Den næste Pythagoras identitet er tangenten:
Såto(α) + 1 = sekto(α)
(3/4) ^ 2 + 1 = 9/16 + 16/16 = (9 + 16) / 16 = 25/16 = (5/4) ^ 2
Og det konkluderes, at tangentens identitet er bekræftet.
- På samme måde som cotangenten:
1 + Ctgto(α) = Cscto(α)
1+ (4/3) ^ 2 = 1 + 16/9 = 25/9 = (5/3) ^ 2
Det konkluderes, at det også er opfyldt, hvormed opgaven med at verificere de pythagoranske identiteter for den givne trekant er afsluttet.
Løst øvelser
Bevis følgende identiteter, baseret på definitionerne af de trigonometriske forhold og de pythagoriske identiteter.
Øvelse 1
Bevis at Costo x = (1 + Sen x) (1 - Sen x).
Opløsning: I højre side genkendes det bemærkelsesværdige produkt ved multiplikation af et binomium med dets konjugat, hvilket som bekendt er en forskel i firkanter:
Costo x = 1to - Sento x
Derefter går udtrykket med sinus på højre side til venstre side med tegnet ændret:
Costo x + Sento x = 1
At bemærke, at den grundlæggende trigonometriske identitet er nået, så det konkluderes, at det givne udtryk er en identitet, dvs. det er sandt for enhver værdi af x.
Øvelse 2
Startende med den grundlæggende trigonometriske identitet og brug af definitionerne af de trigonometriske forhold, demonstrer den Pythagorasiske identitet af cosecanten.
Løsning: Den grundlæggende identitet er:
Sento(x) + Costo(x) = 1
Begge medlemmer er delt mellem Sento(x) og nævneren fordeles i det første medlem:
Sento(x) / Sento(x) + Costo(x) / Sento(x) = 1 / Sento(x)
Det er forenklet:
1 + (Cos (x) / Sen (x)) ^ 2 = (1 / Sen (x)) ^ 2
Cos (x) / Sen (x) = Cotan (x) er en (ikke-Pythagoras) identitet, der verificeres ved definitionen af de trigonometriske forhold. Det samme sker med følgende identitet: 1 / Sen (x) = Csc (x).
Endelig skal du:
1 + Ctgto(x) = Cscto(x)
Referencer
- Baldor J. (1973). Plan- og rumgeometri med en introduktion til trigonometri. Centralamerikansk kultur. AC.
- C. E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende udgave). Pearson Uddannelse.
- Patiño, M. (2006). Matematik 5. Redaktionel Progreso.
- Wikipedia. Trigonometri identiteter og formler. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer