Magnetiske induktionsformler, hvordan det beregnes og eksempler

Det magnetisk induktion eller magnetisk fluxdensitet er en ændring af miljøet forårsaget af tilstedeværelsen af ​​elektriske strømme. De ændrer karakteren af ​​det rum, der omgiver dem, og skaber en landskabet vektor.

Vektoren magnetisk induktion, magnetisk fluxdensitet Eller simpelthen magnetfelt B, den har tre karakteristiske egenskaber: en intensitet udtrykt ved en numerisk værdi, en retning og også en sans givet ved hvert punkt i rummet. Det er fremhævet med fed skrift for at skelne det fra rent numeriske eller skalære størrelser.

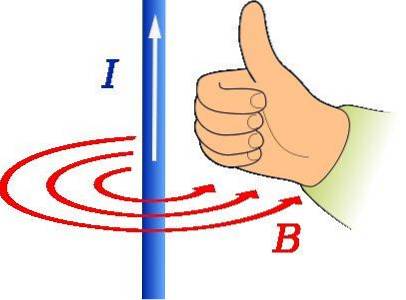
Højre tommelfingerregel bruges til at finde retningen og retningen af ​​magnetfeltet forårsaget af en strømførende ledning som vist i figuren ovenfor.

Tommelfingeren på højre hånd skal pege i retning af strømmen. Derefter angiver rotation af de fire resterende fingre formen på B, som i figuren er repræsenteret af de koncentriske røde cirkler.

I et sådant tilfælde skal adressen på B er tangential til omkredsen koncentrisk med ledningen og er mod uret.

Det magnetisk induktion B I det internationale system måles Tesla (T), men det er hyppigere at måle det i en anden enhed kaldet Gauss (G). Begge enheder blev navngivet henholdsvis til ære for Nikola Tesla (1856-1943) og Carl Friedrich Gauss (1777-1855) for deres ekstraordinære bidrag til videnskaben om elektricitet og magnetisme..

Artikelindeks

• 1 Hvad er egenskaberne ved magnetisk induktion eller magnetisk fluxdensitet?
• 2 Biot-Savarts lov
• 3 formler
• 4 Hvordan beregnes det?
  • 4.1 Eksempel
• 5 Referencer

Hvad er egenskaberne ved magnetisk induktion eller magnetisk fluxdensitet?

Et kompas, der er placeret nær strømførende ledning, vil altid være på linje med B. Den danske fysiker Hans Christian Oersted (1777-1851) var den første, der bemærkede dette fænomen i det tidlige 19. århundrede.

Og når strømmen ophører, peger kompasset som altid mod geografisk nord. Ved omhyggeligt at ændre kompassets position opnås et kort over magnetfeltets form.

Dette kort er altid i form af cirkler koncentrisk til ledningen, som beskrevet i begyndelsen. På denne måde kan du visualisere B.

Selvom ledningen ikke er lige, er vektoren B det vil danne koncentriske cirkler omkring det. For at bestemme feltets form, forestil dig bare meget små ledningssegmenter, så små, at de ser ud retlinede og omgivet af koncentriske cirkler..

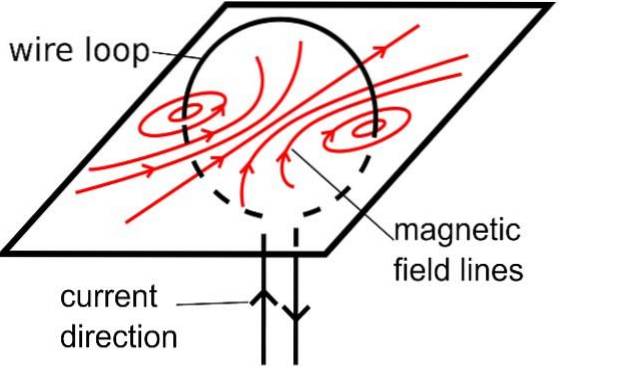
Dette peger på en vigtig egenskab ved magnetfeltlinjer. B: de har ingen begyndelse eller slutning, de er altid lukkede kurver.

Biot-Savarts lov

Det 19. århundrede markerede begyndelsen på alderen for elektricitet og magnetisme inden for videnskab. Omkring år 1820 opdagede de franske fysikere Jean Marie Biot (1774-1862) og Felix Savart (1791-1841) loven, der bærer deres navn, og som giver os mulighed for at beregne vektoren B.

De foretog følgende observationer om bidraget til magnetfeltet produceret af et ledningssegment med forskellig længde dl der bærer en elektrisk strøm jeg:

• Størrelsen af B falder med den inverse firkant af afstanden til ledningen (dette giver mening: væk fra ledningen intensiteten af B skal være mindre end nær punkter).
• Størrelsen af B er proportional med strømens intensitet jeg der går gennem ledningen.
• Adressen til B er tangential til radiusomkredsen r centreret om ledningen og følelsen af B gives, som vi sagde, ved reglen om højre tommelfinger.

Korsproduktet eller krydsproduktet er det passende matematiske værktøj til at udtrykke det sidste punkt. For at etablere et vektorprodukt er der brug for to vektorer, der defineres som følger:

• dl er vektoren, hvis størrelse er længden af ​​det differentielle segment dl
• r er vektoren, der går fra ledningen til det punkt, hvor du vil finde feltet

Formler

Alt dette kan kombineres til et matematisk udtryk:

Den konstante proportionalitet, der er nødvendig for at skabe lighed, er magnetisk permeabilitet af ledig plads μ_eller  = 4π.10^-7 T.m / A

Dette udtryk er Biot og Savart-loven, som giver os mulighed for at beregne magnetfeltet for et aktuelt segment.

Et sådant segment skal igen være en del af et større og mere lukket kredsløb: en strømfordeling.

Betingelsen for, at kredsløbet er lukket, er nødvendigt for at en elektrisk strøm kan strømme. Elektrisk strøm kan ikke strømme i åbne kredsløb.

Endelig, for at finde det totale magnetiske felt for nævnte strømfordeling, tilføjes alle bidrag fra hvert differenssegment dl. Dette svarer til integration over hele distributionen:

For at anvende Biot-Savart-loven og beregne den magnetiske induktionsvektor er det nødvendigt at overveje nogle meget vigtige vigtige punkter:

• Krydsproduktet mellem to vektorer resulterer altid i en anden vektor.

• 

• Det er praktisk at finde vektorproduktet Før at overgå til opløsningen af ​​integralet, så løses integralet af hver af de komponenter, der opnås separat.
• Det er nødvendigt at tegne et billede af situationen og etablere et passende koordinatsystem.
• Hver gang eksistensen af ​​en eller anden symmetri observeres, skal den bruges til at spare beregningstid.
• Når der er trekanter, er Pythagoras sætning og cosinus sætning til stor hjælp til at etablere det geometriske forhold mellem variablerne.

Hvordan beregnes det?

Med et praktisk eksempel på beregning af B for en lige ledning gælder disse anbefalinger.

Eksempel

Beregn magnetfeltvektoren, som en meget lang retlinet ledning producerer ved et punkt P i rummet, ifølge den viste figur.

Fra figuren skal du:

• Ledningen er rettet i lodret retning, hvor strøm I strømmer opad. Denne retning er + y i koordinatsystemet, hvis oprindelse er ved punkt O.

• 

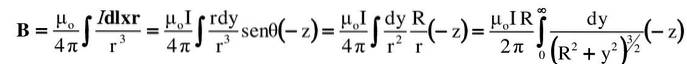
• I et sådant tilfælde i henhold til reglen om højre tommelfinger, B i punkt P er det rettet mod indersiden af ​​papiret, derfor er det betegnet med en lille cirkel og et "x" i figuren. Denne adresse tages som -z.
• Den højre trekant, hvis ben er Y Y R, relatere begge variabler i henhold til Pythagoras sætning: r^to= R^to+Y^to

Alt dette er erstattet af integralet. Korsproduktet eller krydset er angivet med dets størrelse plus dets retning og dets sans:

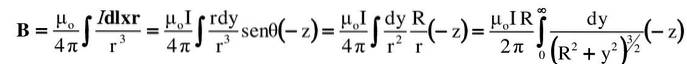
Den foreslåede integral findes i en tabel over integraler, eller den løses ved en passende trigonometrisk erstatning (læseren kan kontrollere resultatet ved hjælp af y = Rtg θ):

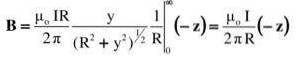
Resultatet stemmer overens med, hvad der var forventet: feltets størrelse falder med afstanden R og øges proportionalt med intensiteten af ​​strømmen I.

Selvom en uendelig lang ledning er en idealisering, er det opnåede udtryk en meget god tilnærmelse til feltet for en lang ledning.

Med Biot og Savarts lov er det muligt at finde magnetfeltet for andre stærkt symmetriske fordelinger, såsom en cirkulær sløjfe, der bærer strøm eller bøjede ledninger, der kombinerer retlinede og krumme linier..

For at analytisk løse den foreslåede integral skal problemet naturligvis have en høj grad af symmetri. Ellers er alternativet at løse integralet numerisk.

Referencer

1. Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 2. Mexico. Cengage Learning Editors. 367-372.