
Ohms lovenheder og formel, beregning, eksempler, øvelser
Det Ohms lov, i sin makroskopiske form indikerer det, at spændingen og intensiteten af strømmen i et kredsløb er direkte proportionale, idet modstanden er proportionalitetskonstanten. Ved at betegne disse tre størrelser som henholdsvis V, I og R siger Ohms lov, at: V = I.R.
Ligeledes er Ohms lov generaliseret til at omfatte kredsløbselementer, der ikke er rent modstandsdygtige i vekselstrømskredsløb, på denne måde tager det følgende form: V = I. Z.

Hvor Z er impedansen, som også repræsenterer modstanden mod passage af vekselstrøm af et kredsløbselement, for eksempel en kondensator eller en induktans.
Det skal bemærkes, at ikke alle kredsløbsmaterialer og -elementer overholder Ohms lov. De, hvor det er gyldigt, kaldes elementer ohmisk, og hvor det ikke er opfyldt, er de ikke-ohmske eller ikke-lineær.
Almindelige elektriske modstande er af ohmsk type, men dioder og transistorer er ikke, da forholdet mellem spænding og strøm ikke er lineært i dem..
Ohms lov skylder sit navn til den bayersk-fødte tyske fysiker og matematiker George Simon Ohm (1789-1854), der tilbragte sin karriere med at studere opførelsen af elektriske kredsløb. Enheden til elektrisk modstand i SI International System er blevet navngivet til hans ære: ohm, som også udtrykkes med det græske bogstav Ω.
Artikelindeks
- 1 Hvordan beregnes det?
- 1.1 Ledningens modstand
- 2 Eksempler
- 2.1 Eksperiment med at kontrollere Ohms lov
- 2.2 Hydraulisk analogi til Ohms lov
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Hvordan beregnes det?
Selvom den makroskopiske form af Ohms lov er den bedst kendte, da den forbinder mængder, der let kan måles i laboratoriet, mikroskopisk form relaterer to vigtige vektormængder: det elektriske felt OG og strømtætheden J:
J = σ.OG
Hvor σ er materialets elektriske ledningsevne, en egenskab der angiver hvor let det er at lede strøm. For hans del J er en vektor, hvis størrelse er kvotienten mellem strømintensiteten I og tværsnitsarealet A, gennem hvilken den cirkulerer.
Det er logisk at antage, at der er en naturlig forbindelse mellem det elektriske felt inde i et materiale og den elektriske strøm, der cirkulerer gennem det, således at jo større strøm, jo mere strøm.
Men strømmen er ikke en vektor, da den ikke har en retning i rummet. I stedet for vektoren J er vinkelret - eller normalt - på lederens tværsnitsareal, og dens retning er strømens retning.
Fra denne form for Ohms lov ankommer vi til den første ligning, idet vi antager en leder med længde ℓ og tværsnit A og erstatter størrelsen af J Y OG til:
J = I / A
E = V / ℓ
J = σ.E → I / A = σ. (V / ℓ)
V = (ℓ / σ.A) .I
Den omvendte ledningsevne kaldes modstand og er betegnet med det græske bogstav ρ:
1 / σ = ρ
Derfor:
V = (ρℓ / A) .I = R.I
Modstanden fra en leder
I ligningen V = (ρℓ / A) .I, konstanten (ρℓ / A) er modstanden, derfor:
R = ρℓ / A
Ledningens modstand afhænger af tre faktorer:
-Dens modstandsdygtighed ρ, typisk for det materiale, som den er fremstillet med.
-Længden ℓ.
-Område A med dets tværsnit.
Jo højere ℓ, jo større er modstanden, da nuværende bærere har flere muligheder for at kollidere med andre partikler inde i lederen og miste energi. Og tværtimod, jo højere A, jo lettere er det for nuværende bærere at bevæge sig ordentligt gennem materialet..
Endelig ligger i det molekylære struktur af hvert materiale den lethed, hvormed et stof tillader den elektriske strøm at passere. Således er f.eks. Metaller som kobber, guld, sølv og platin med lav resistivitet gode ledere, mens træ, gummi og olie ikke er det, hvorfor de har højere resistivitet.
Eksempler
Her er to illustrative eksempler på Ohms lov.
Eksperiment med at kontrollere Ohms lov
En simpel oplevelse illustrerer Ohms lov, til dette har du brug for et stykke ledende materiale, en variabel spændingskilde og et multimeter.
En spænding V etableres mellem enderne af det ledende materiale, som skal varieres lidt efter lidt. Med den variable strømkilde kan værdierne for den nævnte spænding indstilles, som måles med multimeteret, såvel som strømmen I, der cirkulerer gennem lederen..
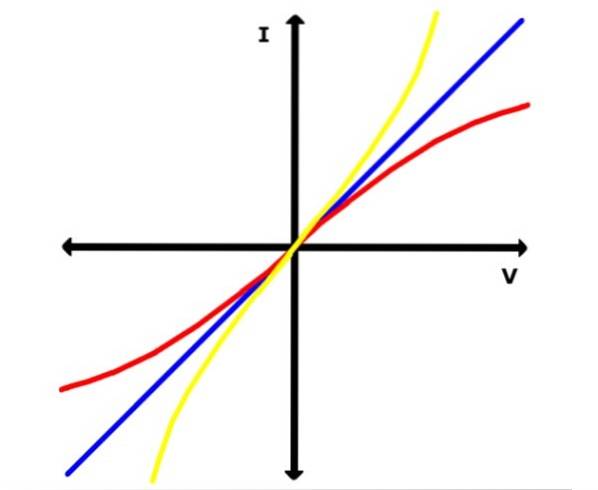
Parene med V- og I-værdier registreres i en tabel, og der konstrueres en graf på grafpapir med dem. Hvis den resulterende kurve er en lige linje, er materialet ohmsk, men hvis det er en anden kurve, er materialet ikke-ohmsk.
I det første tilfælde kan linjens hældning bestemmes, hvilket svarer til lederens modstand R eller dens inverse ledning.
På billedet nedenfor repræsenterer den blå linje en af disse grafer for et ohmsk materiale. I mellemtiden er de gule og røde kurver lavet af ikke-ohmske materialer, som f.eks. En halvleder..
Hydraulisk analogi til Ohms lov
Det er interessant at vide, at den elektriske strøm i Ohms lov opfører sig på samme måde som vand, der strømmer gennem et rør. Den engelske fysiker Oliver Lodge var den første til at foreslå simulering af strømens opførsel ved hjælp af elementer fra hydraulik.
For eksempel repræsenterer rørene lederne, da vandet cirkulerer gennem dem og de nuværende bærere gennem sidstnævnte. Når der er en indsnævring i røret, er vandets passage vanskelig, så dette svarer til en elektrisk modstand.
Forskellen i tryk i to ender af røret gør det muligt for vandet at strømme, hvilket giver en forskel i højden eller en vandpumpe, og ligeledes er forskellen i potentiale (batteriet) det, der holder opladningen i bevægelse., Svarende til strømmen eller volumen vand pr. tidsenhed.
En stempelpumpe ville spille rollen som en alternerende spændingskilde, men fordelen ved at sætte en vandpumpe på er, at det hydrauliske kredsløb således ville være lukket, ligesom et elektrisk kredsløb skal være for at strømmen skal strømme.

Modstande og afbrydere
Ækvivalent til en switch i et kredsløb, det ville være en stophan. Det fortolkes på denne måde: Hvis kredsløbet er åbent (stophanen lukket), kan strømmen, ligesom vandet, ikke strømme.
På den anden side, med kontakten lukket (stophanen helt åben) kan både strømmen og vandet strømme uden problemer gennem lederen eller røret.
Stophanen eller ventilen kan også repræsentere en modstand: når hanen åbnes helt, svarer det til at have en nulmodstand eller en kortslutning. Hvis det lukker helt, er det som at have kredsløbet åbent, mens det delvist er lukket, er det som at have en modstand af en bestemt værdi (se figur 3).
Uddannelse
- Øvelse 1
Et elektrisk jern er kendt for at kræve 2A ved 120V for at fungere korrekt. Hvad er din modstand?
Opløsning
Løs modstand fra Ohms lov:
R = V / I = 120 V / 2 A = 60 Ω
- Øvelse 2
En ledning med en diameter på 3 mm og en længde på 150 m har en elektrisk modstand på 3,00 Ω ved 20 ° C. Find materialets resistivitet.
Opløsning
Ligningen R = ρℓ / A er passende, derfor skal tværsnitsområdet først findes:
A = π(D / 2)to = π (3 x 10-3 m / 2)to = 4,5π x 10 -6 mto
Endelig når du udskifter får du:
ρ = A.R / ℓ = 4,5π x 10 -6 mto x 3 Ω / 150 m = 2,83 x 10 -7 Ω.m
Referencer
- Resnick, R. 1992. Fysik. Tredje udvidede udgave på spansk. Bind 2. Compañía Editorial Continental S.A. af C.V.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14th. Red. Bind 2. 817-820.
- Serway, R., Jewett, J. 2009. Fysik til videnskab og teknik med moderne fysik. 7. udgave. Bind 2. Cengage Learning. 752-775.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. Mcgraw bakke.
- Sevilla Universitet. Institut for Anvendt Fysik III. Densitet og intensitet af strømmen. Gendannet fra: us.es.
- Walker, J. 2008. Fysik. 4. udgave Pearson. 725-728



Endnu ingen kommentarer