Eksponentens love (med eksempler og løste øvelser)

Det love om eksponenter er dem, der gælder for det tal, der angiver, hvor mange gange et basenummer skal ganges med sig selv. Eksponenterne er også kendt som magter. Empowerment er en matematisk operation dannet af en base (a), eksponenten (m) og power (b), som er resultatet af operationen.

Eksponenter bruges generelt, når der anvendes meget store mængder, fordi disse ikke er andet end forkortelser, der repræsenterer multiplikationen af ​​det samme antal et bestemt antal gange. Eksponenter kan være både positive og negative.

Artikelindeks

• 1 Forklaring af eksponentlovene
  • 1.1 Første lov: eksponentens styrke lig med 1
  • 1.2 Anden lov: eksponentens styrke lig med 0
  • 1.3 Tredje lov: negativ eksponent
  • 1.4 Fjerde lov: multiplikation af beføjelser med lige base
  • 1.5 Femte lov: magtfordeling med lige base
  • 1.6 Sjette lov: multiplikation af beføjelser med forskellige baser
  • 1.7 Syvende lov: magtfordeling med forskellig base
  • 1.8 Ottende lov: en magt
  • 1.9 Niende lov: fraktioneret eksponent
• 2 Løst øvelser
  • 2.1 Øvelse 1
  • 2.2 Øvelse 2
• 3 Referencer

Forklaring af lovene om eksponenter

Som nævnt ovenfor er eksponenter en stenografisk form, der repræsenterer at multiplicere tal med sig selv flere gange, hvor eksponenten kun vedrører tallet til venstre. For eksempel:

to³ = 2 * 2 * 2 = 8

I så fald er tallet 2 bunden af ​​strømmen, som ganges 3 gange som angivet af eksponenten, placeret i øverste højre hjørne af basen. Der er forskellige måder at læse udtrykket på: 2 hævet til 3 eller også 2 hævet til terningen.

Eksponenterne angiver også antallet af gange, de kan opdeles, og for at differentiere denne operation fra multiplikation har eksponenten minustegnet (-) foran sig (det er negativt), hvilket betyder, at eksponenten er i nævneren af ​​en brøkdel. For eksempel:

to^{- 4} = 1/2 * 2 * 2 * 2 = 1/16

Dette bør ikke forveksles med det tilfælde, hvor basen er negativ, da det afhænger af, om eksponenten er ulige eller endda for at bestemme, om magten vil være positiv eller negativ. Så du skal:

- Hvis eksponenten er jævn, vil styrken være positiv. For eksempel:

(-7)^to = -7 _* -7 = 49.

- Hvis eksponenten er ulige, vil effekten være negativ. For eksempel:

(-to)⁵ = (-2) * (- 2) * (- 2) * (- 2) * (- 2) = - 32.

Der er et specielt tilfælde, hvor hvis eksponenten er lig med 0, er effekten lig med 1. Der er også muligheden for, at basen er 0; i så fald afhængigt af eksponenten vil strømmen være ubestemt eller ej.

For at udføre matematiske operationer med eksponenter er det nødvendigt at følge flere regler eller normer, der gør det lettere at finde løsningen på disse operationer.

Første lov: eksponentens styrke lig med 1

Når eksponenten er 1, bliver resultatet den samme værdi af basen: a¹ = a.

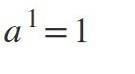
Eksempler

9¹ = 9.

22¹ = 22.

895¹ = 895.

Anden lov: eksponentmagt lig med 0

Når eksponenten er 0, hvis basen ikke er nul, bliver resultatet: a⁰ = 1.

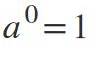
Eksempler

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Tredje lov: negativ eksponent

Da eksponenten er negativ, vil resultatet være en brøkdel, hvor magten vil være nævneren. For eksempel, hvis m er positiv, så er a^-m = 1 / a^m.

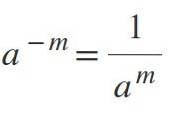
Eksempler

- 3^-1 = 1/3.

- 6^-to = 1/6^to = 1/36.

- 8^-3 = 1/8³ = 1/512.

Fjerde lov: multiplikation af beføjelser med lige base

For at multiplicere kræfter, hvor baserne er lig med og adskiller sig fra 0, forbliver basen, og eksponenterne tilføjes: a^m _* tilⁿ = a^{m + n}.    

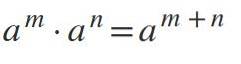
Eksempler

- 4⁴ _* 4³ = 4^{4 + 3} = 4⁷

- 8¹ _* 8⁴ = 8^{1 + 4} = 8⁵

- to^to _* to⁹ = 2^{2 + 9} = 2^elleve

Femte lov: magtfordeling med lige base

For at opdele kræfter, hvor baserne er lig med og adskiller sig fra 0, holdes basen, og eksponenterne trækkes som følger: a^m / tilⁿ = a^m-n.    

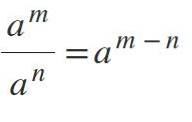
Eksempler

- 9^to / 9¹ = 9 ^(enogtyve) = 9¹.

- 6^femten / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Sjette lov: multiplikation af beføjelser med forskellige baser

I denne lov er der det modsatte af det, der kommer til udtryk i den fjerde; hvis du har forskellige baser, men med de samme eksponenter, multipliceres baserne, og eksponenten opretholdes: a^m _* b^m = (a_*b) ^m.

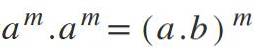
Eksempler

- 10^to _* tyve^to = (10 _* tyve)^to = 200^to.

- Fire. Fem^elleve _* 9^elleve = (45 * 9)^{11 =} 405^elleve.

En anden måde at repræsentere denne lov er, når en multiplikation hæves til en magt. Eksponenten hører således til hvert af udtrykkene: (a_*b)^m= a^m_* b^m.

Eksempler

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Syvende lov: magtfordeling med forskellig base

Hvis du har forskellige baser, men med de samme eksponenter, skal du dele baserne og beholde eksponenten: a^m / b^m = (a / b)^m.

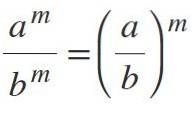
Eksempler

- 30³ / to³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

Tilsvarende, når en division hæves til en magt, vil eksponenten høre hjemme i hvert af udtrykkene: (a / b) ^m = a^m / b^m.

Eksempler

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)^to = 25^to / 5^to = 5^to.

Der er tilfældet, hvor eksponenten er negativ. For at være positiv inverteres tællerens værdi med nævneren som følger:

- (a / b)^-n = (b / a)ⁿ = bⁿ / tilⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Ottende lov: magtens magt

Når du har en magt, der hæves til en anden magt - det vil sige to eksponenter på samme tid - opretholdes basen, og eksponenterne multipliceres: (a^m)ⁿ= a^{m *n}.

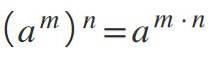
Eksempler

- (8³)^to = 8 ^{(3 * 2)} = 8⁶.

- (13⁹)³ = 13 ^{(9 * 3)} = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Niende lov: fraktioneret eksponent

Hvis magten har en brøkdel som en eksponent, løses dette ved at omdanne den til en n. Rod, hvor tælleren forbliver som en eksponent, og nævneren repræsenterer indekset for roden:

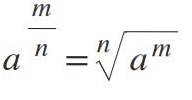
Eksempel

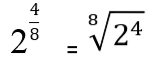
Løst øvelser

Øvelse 1

Beregn operationerne mellem de kræfter, der har forskellige baser:

to⁴ _* 4⁴ / 8^to.

Opløsning

Ved anvendelse af reglerne for eksponenter multipliceres baserne i tælleren, og eksponenten opretholdes på denne måde:

to⁴ _* 4⁴ / 8^to= (2_*4)⁴ / 8^to  = 8⁴ / 8^to

Nu, da vi har de samme baser, men med forskellige eksponenter, holdes basen, og eksponenterne trækkes fra:

 8⁴ / 8^to = 8^{(4 - 2)} = 8^to

Øvelse 2

Beregn operationerne mellem beføjelserne til en anden magt:

(3^to)³ _* (to _* 6⁵)^-to _* (to^to)³

Opløsning

Når du anvender lovene, skal du:

(3^to)³ _* (to _* 6⁵)^-to _* (to^to)³

= 3⁶ _* to^-to _* to^-10 _* to⁶

= 3⁶ _* to^{(-2) + (- 10)} _* to⁶

= 3⁶ _*  to^-12 _* to⁶

= 3⁶ _* to^{(-12) + (6)}

= 3⁶ _* to⁶

= (3_*to)⁶

= 6⁶

= 46,656

Referencer

1. Aponte, G. (1998). Grundlæggende grundlæggende matematik. Pearson Uddannelse.
2. Corbalán, F. (1997). Matematik anvendt i hverdagen.
3. Jiménez, J. R. (2009). Matematik 1 SEP.
4. Max Peters, W. L. (1972). Algebra og trigonometri.
5. Rees, P. K. (1986). Vend tilbage.