
Klassemarkør Hvad det er til, hvordan man får det og eksempler
Det klassemærke, Også kendt som midtpunktet er det værdien, der er i midten af en klasse, der repræsenterer alle de værdier, der er i den kategori. Grundlæggende bruges klassemærket til at beregne bestemte parametre, såsom det aritmetiske gennemsnit eller standardafvigelsen..
Klassemærket er altså midtpunktet for ethvert interval. Denne værdi er også meget nyttig til at finde variansen af et sæt data, der allerede er grupperet i klasser, hvilket igen giver os mulighed for at forstå, hvor langt fra centrum disse specifikke data er placeret.

Artikelindeks
- 1 Frekvensfordeling
- 1.1 Hvor mange klasser skal overvejes?
- 2 Hvordan får du det?
- 2.1 Eksempel
- 3 Hvad er det til??
- 3.1 Eksempel
- 4 Referencer
Frekvensfordeling
For at forstå, hvad et klassemærke er, er begrebet frekvensfordeling nødvendig. Med et sæt data er en frekvensfordeling en tabel, der opdeler dataene i et antal kategorier kaldet klasser..
Den nævnte tabel viser mængden af elementer, der hører til hver klasse; sidstnævnte er kendt som frekvens.
I denne tabel ofres en del af den information, vi får fra dataene, da vi i stedet for at have den individuelle værdi for hvert element kun ved, at det hører til den klasse.
På den anden side får vi en bedre forståelse af datasættet, da det på denne måde er lettere at værdsætte etablerede mønstre, hvilket letter manipulationen af de nævnte data..
Hvor mange klasser skal overvejes?
For at foretage en frekvensfordeling skal vi først bestemme antallet af klasser, vi vil tage, og vælge deres klassegrænser..
At vælge, hvor mange klasser, der skal tages, skal være praktisk, idet man tager i betragtning, at et lille antal klasser kan skjule oplysninger om de data, vi vil studere, og en meget stor kan generere for mange detaljer, der ikke nødvendigvis er nyttige.
De faktorer, som vi skal tage i betragtning, når vi vælger, hvor mange klasser vi skal tage, er flere, men blandt disse to skiller sig ud: den første er at tage højde for, hvor meget data vi skal overveje; det andet er at vide, hvor stort distributionsområdet er (det vil sige forskellen mellem den største og mindste observation).
Efter at klasserne allerede er defineret, tæller vi, hvor meget data der findes i hver klasse. Dette nummer kaldes frekvensen af klasser og betegnes med fi.
Som vi tidligere har sagt, har vi, at en frekvensfordeling mister de oplysninger, der kommer individuelt fra hver data eller observation. Af denne grund søges en værdi, der repræsenterer hele klassen, som den tilhører; denne værdi er klassemærket.
Hvordan opnås det?
Klassemærket er kerneværdien, som en klasse repræsenterer. Det opnås ved at tilføje grænserne for intervallet og dividere denne værdi med to. Vi kunne udtrykke dette matematisk som følger:
xjeg= (Nedre grænse + Øvre grænse) / 2.
I dette udtryk xjeg angiver mærket for i-th-klassen.
Eksempel
Givet det følgende datasæt, giv en repræsentativ frekvensfordeling og få karakteren for de tilsvarende klasser.

Da data med den højeste numeriske værdi er 391 og den laveste er 221, har vi, at området er 391-221 = 170.
Vi vælger 5 klasser, alle med samme størrelse. En måde at vælge klasser på er som følger:

Bemærk, at hver data er i en klasse, disse er uensartede og har samme værdi. En anden måde at vælge klasser på er ved at betragte dataene som en del af en kontinuerlig variabel, som kan nå enhver reel værdi. I dette tilfælde kan vi overveje klasser af formularen:
205-245, 245-285, 285-325, 325-365, 365-405
Denne måde at gruppere data på kan dog præsentere nogle grænseværdige tvetydigheder. For eksempel i tilfælde af 245 opstår spørgsmålet: hvilken klasse tilhører den, den første eller den anden?
For at undgå denne forvirring foretages en slutpunktskonvention. På denne måde vil den første klasse være intervallet (205,245], det andet (245,285] osv..

Når klasserne er defineret, fortsætter vi med at beregne frekvensen, og vi har følgende tabel:
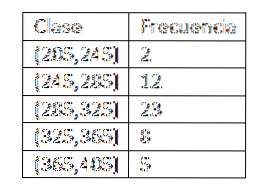
Efter at have opnået frekvensfordelingen af dataene fortsætter vi med at finde klassemarkeringerne for hvert interval. Vi er faktisk nødt til at:
x1= (205+ 245) / 2 = 225
xto= (245+ 285) / 2 = 265
x3= (285+ 325) / 2 = 305
x4= (325+ 365) / 2 = 345
x5= (365+ 405) / 2 = 385
Vi kan repræsentere dette ved hjælp af følgende graf:
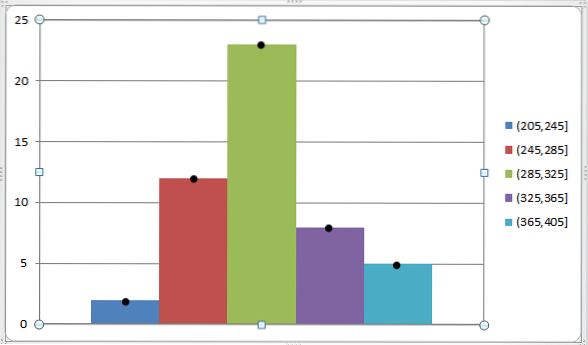
Hvad er det for?
Som tidligere nævnt er klassemærket meget funktionelt til at finde det aritmetiske gennemsnit og variansen af en gruppe data, der allerede er grupperet i forskellige klasser..
Vi kan definere det aritmetiske gennemsnit som summen af de observerede observationer mellem stikprøvestørrelsen. Fra et fysisk synspunkt er dens fortolkning som ligevægtspunktet i et datasæt.
At identificere et helt datasæt med et enkelt nummer kan være risikabelt, så forskellen mellem dette breakeven-punkt og de faktiske data skal også tages i betragtning. Disse værdier er kendt som afvigelse fra det aritmetiske gennemsnit, og med disse søger vi at bestemme, hvor meget det aritmetiske gennemsnit af dataene varierer..
Den mest almindelige måde at finde denne værdi på er variansen, som er gennemsnittet af kvadraterne for afvigelserne fra det aritmetiske gennemsnit.
For at beregne det aritmetiske gennemsnit og variansen af et datasæt grupperet i en klasse bruger vi henholdsvis følgende formler:
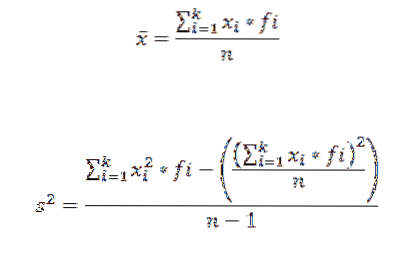
I disse udtryk xjeg er det i-klassemærke, fjeg repræsenterer den tilsvarende frekvens og k antallet af klasser, hvori dataene blev grupperet.
Eksempel
Ved at bruge de data, der er givet i det foregående eksempel, har vi, at vi kan udvide lidt mere dataene i frekvensfordelingstabellen. Du får følgende:
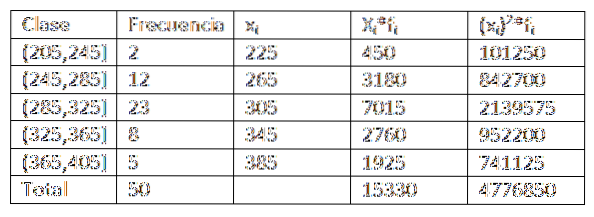
Derefter, ved at erstatte dataene i formlen, er vi tilbage, at det aritmetiske gennemsnit er:
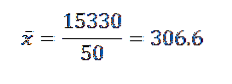
Dens varians og standardafvigelse er:
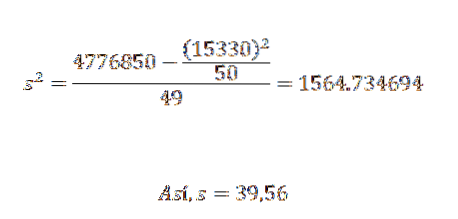
Ud fra dette kan vi konkludere, at de originale data har et aritmetisk gennemsnit på 306,6 og en standardafvigelse på 39,56..
Referencer
- Fernandez F. Santiago, Cordoba L. Alejandro, Cordero S. Jose M. Beskrivende statistik. Esic Editorial.
- Johnson Richard A. Miller og Freund Probability and Statesmen for Engineers, Pearson Education.
- Miller I & Freund J. Probability and Statesmen for Engineers. VENDE TILBAGE.
- Sarabia A. Jose Maria, Pascual Marta. Grundlæggende statistik kursus for virksomheder
- Llinás S. Humberto, Rojas A. Carlos Beskrivende statistik og sandsynlighedsfordeling, Universidad del Norte Editorial



Endnu ingen kommentarer